| Slide rules HOME page | INSTRUCTIONS | MANUALS | < SITE MAP > |
Instructions for use
Multiplication and Division (C and D scales)
Division
Multiplication
Compound multiplication
and division
Continuous multiplication or division and
the Reciprocal scale (CI scale)
p displaced C and D scales
(CF and DF scales)
Determination of Square Roots (A and B scales)
Determination of Cube Roots (K scale)
Determination of Logarithms (L scale)
Orthodox Trigonometrical scales (S, ST and T
scales)
Differential Trigonometrical scales (Sd,
Td, ISd, ITd scales)
Gauge Marks V, U, m, s
Log Log scales (LL3, LL2, LL1 and LL03, LL02, LL01 scales)
Differential Log Log Scales
The L constant on C scale
Vector Analysis scales of Ö(1-s2)
and Ö(1 + t2 ) (Ps and Pt scales)
Cursors
Appendix : Tacheometric Surveying
Care and attention
Removing the cursor
Cleaning the slide rule
Major historical developments in the evolution of the slide rule
Preface
This slide rule has been manufactured after a comprehensive study of the
functional requirements involved and forms part of a new range designed for maximum
efficiency. An outstanding design feature of this range is the introduction of end caps
for holding the two stocks rigidly in relation to each other. These end caps are a major
development in slide rule manufacturing technique. In addition to their primary function
they enable the user to hold the slide rule by them and the recommended method of use is
as follows:
(a) Hold the slide rule by the end caps.
(b) When the slide is virtually fully contained in the two stocks manipulate the slide by the index fingers.
(c) When the slide is extended to one end hold the rule by the end cap at the opposite end and manipulate the slide with the free hand.
In this way lateral pressure across the width of the slide rule is avoided and highest practicable accuracy standards maintained.
If treated with reasonable care and attention your slide rule will give you many years of good service.
This instruction booklet deals with the use of the slide rule in separate stages for each major purpose and covers the main uses comprehensively. Certain portions may not apply to your particular slide rule as you may not have the scales involved - or if you have the scales they may not be relevant to the calculations in which you are interested. Thus if your slide rule has trigonometrical scales and you are not concerned with trigonometrical calculations then the stages dealing with these scales can be omitted.
The purpose of having an instruction booklet covering the main uses is to help readers to see more readily the very wide variety of calculations where the slide rule can be of valuable assistance.
The instructions cover all models in the British Thornton 250mm (10 inch) range and reference to scale subdivisions are based on this range.
1 Introduction
It is easy to use a Slide Rule even though it may take practice to become really familiar with it. In using the various scales you will find it helpful to work out a simple problem which you can check mentally before going on to more complicated calculations. In this way confidence and a proper understanding of the scales is quickly built up, together with an appreciation of the very great use which can be made of the slide rule.
Do not try to use the more advanced scales before you understand the basic scales and make a practice of rough checking your answer mentally - ask yourself 'Does it look right?' - and you will soon join the widening circle of slide rule initiates.
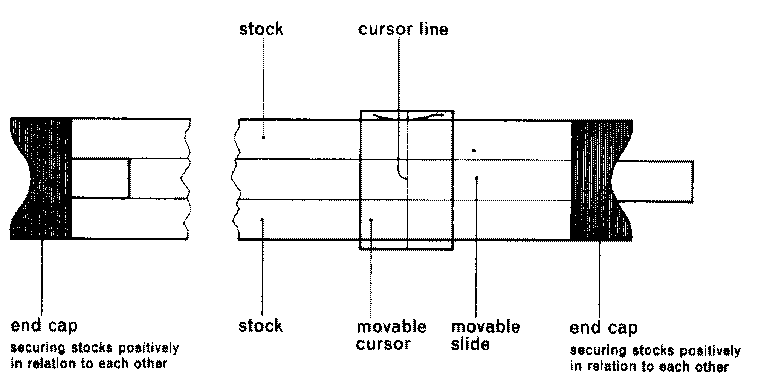
2 Parts of the slide rule
To ensure that we understand the terminology here are the main parts of the slide rule.

3 Significant figures
A slide rule can be regarded normally as giving the answer to a calculation to an
accuracy of three significant figures (although sometimes a fourth significant figure can
be read off). Significant figures do not have anything to do with the decimal point and
must not be confused with it. If we take 276 as an illustration of three significant
figures then 27,600; 276; 27.6; 0.276; 0.00276 are all examples of these three significant
figures. Similarly with 408 as our three significant figures examples are 40,800; 4.08;
0.0408. Thus the number of "0's" to the left of the first significant figure or
to the right of the third significant figure do not affect the significant figures
themselves.
4 Decimal point
Now a word about the position of the decimal point. Usually you know the
approximate value of your answer and therefore the position of the decimal point - if
there is any doubt then do a rough calculation and decide the position of it by
estimation.
5 C and D scales
Let us ignore all scales except the two identified by the letters C and D and
which are located on the slide and stock respectively These two scales are the most
frequently used on a slide rule and are the basic scales normally used for multiplication,
division, ratios etc.
When we inspect these C and D scales closely we note that they are numbered from left to right viz., 1,11,12 and so on 2, 3, 4, 5 to 10. You will probably find it easier to imagine the numbering as 100,110,120 . . . 200, 300, 400, 500 . . . to 1,000 as this will help you in reading and setting the first three significant figures of numbers. The following illustration shows the settings for various significant figure values :
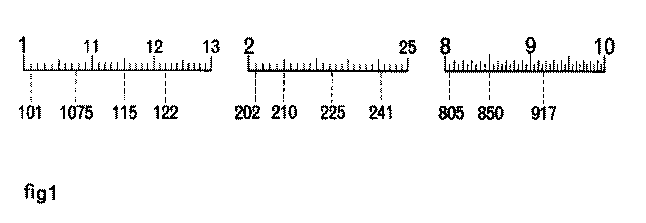
Notice how values between adjacent lines sub-dividing the scale change as we move along the scale. At the beginning the sub-divisions run 1,101, 102, 103, 104, 105 etc up to 110 - thus giving a change of 1 in the third significant figure- and continue in this way up to the 2 position. The scale then runs 2, 202, 204 etc., thus giving a change of 2 in the third significant figure and further along the scale the change in third significant figure is 5. These changes in the values of sub-divisions on the various scales of the slide rule must be constantly observed.
The C and D scales are logarithmic scales numbered naturally. This accounts for the fact that the distance between 1 and 2 is greater than the distance between 2 and 3 which in turn is greater than the distance between 3 and 4 and so on to 10. But the important thing to realise is that these logarithmic scales are of uniform proportional accuracy. A displacement of the C scale in relation to the D scale gives a fixed proportional relationship for all points In alignment. This can be seen by moving the slide to the right so that 1 on C scale is over 2 on D scale and observing that opposite 2 on C scale we have 4 on D scale opposite 3 on C we have 6 on D etc., thereby giving a portion of the two times table. Similarly by setting 1 on C scale over 3 on D scale we have a portion of the three times table.
Now we are ready to commence using our slide rule.
This is carried out by subtracting one logarithmic length (the divisor) from another (the dividend).
Example I
Evaluate - 84 / 24
Set the cursor at 84 on the D scale (referred as D84) and move the slide so that 24 on the C scale (referred to as C24) aligns with the cursor line. At 1 on C scale (referred to as C1) read 35 on the D scale i.e. the significant figures of the answer.
Decimal point considered = 3.5
Example 2
Evaluate - 30.6 / 68
Set the cursor at 306 on the D scale and move the slide so that 68 on the C scale aligns with the cursor line. At 10 on C scale read 45 on the D scale, the significant figures of the answer.
Decimal point considered = .45
The two examples only differ in the respect that in example 1 the answer aligns with C1 on the D scale and in example 2 the result is found at C10.
This is carried out by adding together the logarithmic lengths which correspond to the numbers.
Example 3 Evaluate 2.6x 3.5
Move the slide bringing C1 to D26 set the cursor at C35 and read on the D scale 91, the
significant figures of 2.6 x 3.5.
Decimal point considered 2.6 x 3.5 = 9.1
Example 4 Evaluate 3.25x 4.4
Cursor to D325, C10 to cursor, cursor to C44 and read 143 on the D scale the significant
figure value of 3.25 x 4.4, decimal point considered 14.3.
Again it will be noted that the only difference between examples 3 and 4 is in respect of applying either C1 or C10 the choice being such as to bring the second factor within the D scale range
COMPOUND MULTIPLICATION AND DIVISION
The same principle applies of adding and subtracting logarithmic lengths corresponding to the numbers
The general rule is
FIRST numerator value is set on the D scale
ALL OTHER numerator and denominator values are set on the slide (thus adding or subtracting them from the logarithmic length of the first numerator value)
ANSWER is read on the D scale
Movement of the CURSOR carries out MULTIPLICATION
Movement of the SLIDE carries out DIVISION and these operations must take place ALTERNATELY
If the CURSOR is moved last the result is read at the cursor on D scale
If the SLIDE is moved last the result is read on the D scale against the C1 or C10 line
Example 5 Find the value of::
(161 x 923 x 152) / (258 x 172)
| Instruction | Stage | Significant figures of result on D scale at: | ||
| C1 | C10 | Cursor | ||
| (i) Set cursor at D161 | 161 | |||
| (ii) Move slide bringing C258 to the cursor | 161/ 258 | 624 | ||
| (iii) Cursor to C923 | (161x923)/258 | 576 | ||
| (iv) Move slide bringing C172 to the cursor | (161 x923) / (258x172) | 335 | ||
| (v) Cursor to C152 | (161 x 923 x 152) / (258 x172) | 509 | ||
decimal point considered 509.0
In the next example, if we take the factors in the order in which they occur, alternating from numerator to denominator etc., what is known as an 'end switch' occurs as one of the factors on the slide to which it is desired to move the cursor extends beyond the end of the stock of the rule. The method involved for end switching is simply as follows:
When the slide protrudes to the left of the stock move the cursor to C10 and then 'end switch' the slide by bringing C1 to the cursor. If the slide protrudes to the right of the stock move the cursor to C1and then 'end switch' the slide by bringing C10 to the cursor
'End switching' does not affect the accuracy of the answer as it is simply the equivalent of multiplying or dividing by 1 or 10 and the significant figures remain the same
Example 6 Find the value of::
(.0535 x 741.0 x 4.87) / ( .1925 x .0524 )
| Instruction | Stage | Significant figures of result on D scale at: | ||
| C1 | C10 | Cursor | ||
| (i) Set cursor at D535 | 535 | |||
| (ii) Move slide C1925 to cursor 'End switch' |
535 / 1925 | 278 | ||
| (iii) Cursor to C11 | ||||
| (iv) Move slide C10 to cursor | ||||
| (v) Cursor to C721 | (535x 741) / 1925 | 206 | ||
| (vi) Move slide C524 to cursor | (535x 741) / (1925 x 524) | 393 | ||
| (vii) Cursor to C487 | (535x 741 x487) / (1925 x 524) | 1914 | ||
decimal point considered 19140.0
From the preceding examples it will be seen that for continued multiplication or continued division - using C and D scales only - we must divide or multiply by unity or 10 as required.
Thus (using C and D scales only)
m x n x p
should be manipulated as: m ¸ (1 or 10) x n ¸ (1 or 10) x p
Example 7 Evaluate .0613 x 19.25 x .245 x 56.4
| (i) Cursor to D613 | (ii) C10 to cursor | (iii) Cursor to C1925 |
| (iv) C1 to cursor | (v) Cursor to C245 | (vi) C10 to cursor |
| (vii) Cursor to C564 and on the D scale read 163 the significant figure value of the continuous multiplication; decimal point considered 16.3 | ||
Similarly 1/ (q x r x s)
should be worked as:
(1 or 10) ¸ q x (1 or 10) ¸ r x (1 or 10) ¸ s
Example 8 Find the value of
1/ (17.62 x .846 x 3.15)
| (i) C17.2 to D1 | (ii) Cursor to C10 | iii) C846 to cursor |
| (iv) Cursor to C10 | (v) C315 to cursor and read at C1 on the D scale 213; decimal point considered .0213 | |
Examples 7 and 8 have been worked in order to contrast with examples 9 and 10 using the available additional Reciprocal of C scale (on the slide) in conjunction with the C and D scales
CONTINUOUS MULTIPLICATION OR DIVISION
Using the Reciprocal of C scale (CI) in conjunction with the normal C and D scales. This reciprocal scale runs in the reverse direction to the C and D scales.
The form: m x n x p
must be treated as
m ¸ (1/n) x p
the 1/n being the n value on the Reciprocal Scale (CI)
Example 9 Evaluate .0613x19.25x .245x 56.4
treat as .0613 ¸ (1/19.25) x
.245 ¸ (1/56.4)
| (i) Cursor to D613 | (ii) CI1925 to cursor | (iii) Cursor to C245 |
| (iv) CI564 to cursor and at C1 on the D scale read 163; decimal point considered 16.3 | ||
Note only four settings required in place of seven in the corresponding example 7
Similarly: 1 /(q x r x s)
must be treated as
1 ¸ q x (1/r) ¸ s
Example 10 Find the value of
1/ (17.62 x .846 x 3.15)
| (i) CI1762 to D10 | (ii) Cursor to CI846 | (iii) C315 to Cursor and read at C1 on the D scale 213; decimal point considered .0213 |
Note the three settings in place of five required in example 8
Apart from the additional use of the Reciprocal Scale to obtain reciprocals by cursor projection from the C to the CI scale, other uses will occur to the user in relation to his particular computations.
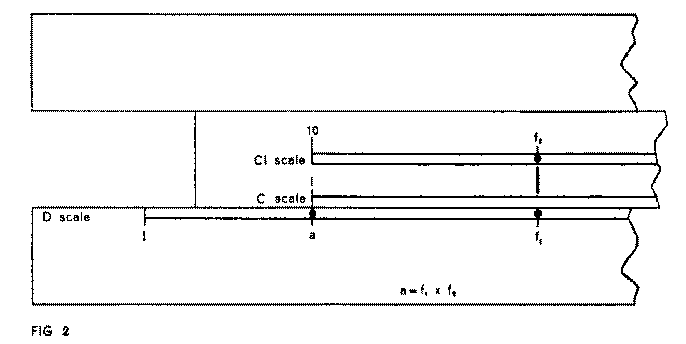
One relationship which merits special mention is:
Where a = f1 x f2 and 'a' is fixed, to determine any of the infinite pairs of values of f1
and f2 that will satisfy (see fig. 2). Arrange slide so that C1(or C10) is at value 'a' on
the D scale Using the Cursor for alignment from one factor on D scale, read other factor
on the C1 scale. Particular care must be taken, when using the Reciprocal of C scale, to
keep in mind the reverse direction of ascending significant figures
These scales are included on certain models of slide rules and occupy the position normally used for the A and B scales with DF on the stock and CF on the slide. These two scales are simply C and D scales displaced by the factor p, and they have particular advantages in multiplication, division, proportions, etc, as they give complete factor range in conjunction with C and D scales
This will be more easily appreciated by comparing the movements involved in a calculation using:
(a) C and D scales only
(b) CF and DF scales in conjunction with C and D
Complete Divisor Range
Example 11
Where a + b +c + d + e = T
express a, b, c, d, e as percentages of T given the following values:
a = 41.3, b = 25.8, c = 89.4, d = 128, e = 84.5 and T = 369
(a) Using C and D scales only
Move slide so that C369 aligns with D1
Then for values 41.3, 84.5 and 89.4
move the cursor to
| (i) C413 | (ii) C845 | (iii) C894 |
| and read the corresponding percentages on the D scale, viz. | ||
| 11.20 % | 22.9 % | 24.2 % respectively |
To obtain the remaining percentages for 128 and 25.8 it is necessary to move the slide so that C369 aligns with D10, when they can be read by moving the cursor to
| (iv) C128 | (v) C258 |
| 34.7 % | 7.00 % |
(b) Using DF, CF, C and D scales
Move the slide so that CF369, aligns with DF10
With the slide in this position all values can be obtained by cursor projection, viz.:
41.3, 84.5 and 89.4 from CF to DF scale 128 and 25.8 from C to D scale
The next example shows how a given factor can be applied to a series of numbers
Example 12
Multiply each of the following numbers: 12.7, 559, 173, 76.8, 24.6, 9.24 and 35.4 by .263
Using the combination DF and CF, C and D scales all the results can be obtained by a
single displacement of the slide and relevant cursor projections viz.:
Move slide so that CF10 aligns with DF263
With the slide in this position all values can be obtained by cursor projection as
follows:
From CF to OF scale- the products of
| (i) 559 | (ii) 76.8 | (iii) 9.24 are read as | |
| 147 | 20.2 | 2.43 respectively | |
| and from C to D scale- the products of | |||
| (iv) 12.7 | (v) 173 | (vi) 24.6 | (vii) 35.4 read as |
| 3.34 | 45.5 | 6.47 | 9.31 |
Two positions of the slide would have been necessary in the above example if only C and D scales were used.
The next example deals with the familiar form
a x b/ c
Using C and D scales only, an 'end switch' is frequently necessary- as is the case in the example below- whereas with the combined displaced scales the 'end switch' can always be avoided by proper selection of the scale to which the initial factor 'a' is applied (i.e. a choice between D or DF).
The correct scale to choose is that which results in more than half the slide engaging in the stock of the slide rule after the divisor has been set
Example 13
3.1 x 8.15/ 1.64
Evaluate
(a) Using C and D scales only- and following normal practice
| (i) Cursor to D31 | (ii) C164 to cursor | (iii) End switch bringing cursor to C1and then C10 to cursor |
| (iv) Cursor to C815 | (v) Read at the cursor 154 on D scale After considering the decimal point 15.4 | |
(b) Using DF, CF, C and D scales
| (i) Cursor to D31 | (ii) C164 to cursor | (iii) Cursor to CF815 |
| (iv) Read at the cursor 154 on DF scale. Decimal point considered=15.4 | ||
It must be borne in mind that a switch from the C, D pair of scales to the CF, DF pair of scales (and vice versa) is made when moving the cursor and not when moving the slide
Whilst the combination of the four scales minimises the need for 'end switching' it must not be concluded that it completely eliminates it in all cases of continuous compound calculations. With experience, by visualising the slide position before moving it, the user may often be able to select factors in an order, or choose scales to ensure that, after division, more than half of the slide is engaged with the stock. This will then mean that on either CF or C scales a complete significant figure range is in contact with either DF or D, thus enabling the cursor to be moved to the next factor without the need of an 'end switch'
Note- It will be appreciated that cursor projection from C and D scales to CF and DF is the equivalent of multiplication by p of the C or D scale value. Thus circumference from diameter of circle (and vice versa) can be obtained at a single setting of the cursor
It will be observed that Scale A of two 1/2 unit sections is arranged in
relation to the D scale (unit length) so that:
A1 aligns with D1
A100 aligns with D10
Using the cursor for projection from D scale to A scale the following alignments can be observed
(a) for involution
| D | 1 | 2 | 3 | 4 | 5 | etc | 10 |
| A | 1 | 4 | 9 | 16 | 25 | etc | 100 |
i.e. 'Squares' of values on D are in alignment on A
(b) for evolution, a reverse process provides 'square roots' of the values on A in alignment with D scale
Since each section, viz. 1 to 10 and 10 to 100, of the A scale provides a full cycle of significant figure range, in the case of square roots' the user has to decide which of the two sections is applicable to any particular evaluation
Consider numbers whose significant figure value is 2788, such values may occur in various forms as .0002788, .002788, etc or 278.8, 278800, etc
By way of illustration let us consider determination of the square roots of three of
these say :
Ö (.0002788), Ö
(278.8) and Ö (278800)
Starting from the decimal point arrange bars under pairs of numbers as shown
| (1) | .00 02 78 80 | |
| (la) | 2 78 |
.80 |
| (2) | 27 88 00 |
. |
(1) and (la) are alike in the respect that the first significant figure 2 is alone over a bar, whereas in (2) the first two significant figures, that is 27, occur under the same bar. In cases such as (1) or (la) projection is from the first section of the A scale whilst case (2) calls for projection from the 2nd Section
Evaluate Ö |
(.00 | 02 | 78 | 8) |
| 0 | 1 | 6 | 7 |
Cursor to 2788 on 1st Section of A scale and read on D scale 167
Again consider the pairs, and with cipher or figure in the result for each pair, the significant figure 167, decimal point considered becomes .0167
Evaluate Ö |
(2 | 78 | .8 |
| 1 | 6 | 7 |
Cursor to 2788 on 1st Section of A and read on D scale 167 This significant figure value 167, decimal point considered, becomes 16.7
Evaluate Ö |
(27 | 88 | 00.) |
Cursor to 2788 on the 2nd Section of A scale and read on D scale 528
This significant figure group 528, decimal point considered, becomes 528.0
After a little practice, the bars for pairing figures can be imagined and so the figure of a 'square root' together with its denomination, can readily be obtained by inspection
Models which incorporate a Cube Root scale denoted by K furnish a direct means of obtaining cube roots by cursor projection. The scale comprises three repeats of a 1/3 unit but care must be exercised in selection of the section to be used
Cube roots of numbers from 1 to 1000 are read off the D scale (C scale if the cube root
scale is on the slide) by cursor projection from the K scale. For numbers above or below 1
to 1000 it is advisable to consider them in groups of three from the decimal point. Then
the following basis can be applied:
One significant figure in excess of complete groups of three- use
first section of K scale
Two significant figures in excess of complete groups of three- use
second section of K scale
No significant figure in excess of complete groups of three- use
third section of K scale
e.g. Evaluate 41780 and .04178
in both cases the two significant figures in excess of complete triads
indicate the use of the second section of K scale from which we obtain 34.7 and 0.347
respectively as the cube roots
The Logarithm scale denoted by L is a uniform scale related to the C and D scales and provides logarithms to base 10.
If we assign the definite values 1.0 to 10.0 to the significant figure scales C and D, then the length of L scale equals that of C or D from 1.0 to 10 and the extremes of the L scale are numbered 0 to 1.0 (Sub-divisions are in accord with decimal reading)
This combination functions as the equivalent of logarithm and antilog tables
To determine log105.2
Use the cursor to project from D52 (C52 if L scale is on the slide) to
the L scale and read Log105.2=.716
The reverse process provides logarithm to number conversions
As with 'log' tables, only the 'mantissa' portion is obtainable from the rule and so in all cases, according to the position of the decimal point, the appropriate 'characteristic' must be applied
ORTHODOX TRIGONOMETRICAL SCALES
These scales are: Sine scale, denoted by S, for the angle range 5.7 to 90° ; Tangent scale, denoted by T, for the angle range 5.7 to 45°; Sine and Tangent scale, denoted by ST, for the angle range 0.57 to 5.7°.
All three scales are decimally sub-divided, are related to the C and D scales and values are read off directly by cursor projection
e.g. Determine the value of Sine 20°
Set cursor to 20° on Sine scale and read on D scale at the cursor 342.
Decimal point considered Sine 20° = .342
e.g. Determine Cos 16°
Since Cos 16° = Sine 74° treat as Sin 74°
Set cursor to 74° on Sine scale and read on D at the cursor 0.961 (the
value of Sin 74° = Cos 16°)
e.g. Determine Tan 22°
Set cursor to 22° on Tan scale and read on D scale 0.404 = Tan 22°
Note: For tangents of angles between 45° and 90° use the formula
Tana = 1/ Tan(90 - a
) = Cot (90- a )
i.e. for Tan 75° set cursor to 15° on Tan scale and on DI read 3.73= Tan
75° (if there is no DI scale then read on CI but see that C & D scales are aligned)
It will be appreciated that determination of the angle when the function value is given involves the inverse of the above process
e.g. To find the angle whose Sine is 0.41 Set cursor to D41 and read on S scale at the cursor 24.2°.
The Sine and Tangent scale (ST) is used for both Sines and Tangents for the lower angle range below 5.7° and is the geometric mean of the two functions. In this respect it will be appreciated that Sin a » Tan a » a in radians when a is small. Thus this scale may be used for converting degrees to radians and vice versa
Note: For small angles care is required in positioning the decimal point when reading answers on D scale, and in the selection of the appropriate angle scale when the function value is given. As a guide the following rule is useful: If the angle is on the ST scale then .0 will precede the significant figures read off the D scale. If the function value on D scale is preceded by .0 then the angle is read on the ST scale
It is important to remember the Sine rule
a / sinA = b / sin B = c / sin C
as these proportions can be usefully applied. It will be appreciated that if a given angle on the Sine scale is aligned with its respective given side on the C scale, then the other pairs of values are also in alignment. Thus if one of each of the other pairs is known the triangle can be solved by cursor projection between the Sine scale and the C scale
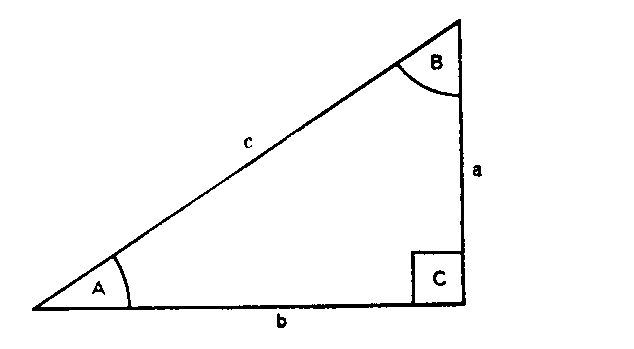
The Sine rule becomes: a / sinA = b / sin B = c / 1
Case 1
Given Angle A = 35.3° and side c = 533
To find sides a and b
Then a / Sin 35.3 = b / Sin (90- 35.3) = 533/1
(a) Set C533 to D10
(b) Cursor to 35.3 on Sine scale and read on C scale 308= side a
(c) Cursor to (90- 35.3) = 54.7 on Sine scale and read on C scale 435 =
side b
Case 2
Given a= 207 and c= 305
To find Angle A and side b
Then 207/ sin A = b / sin B = 305 / 1
(a) Set C305 to D10
(b) Cursor to C207 and read on the Sine scale 42.75 = Angle A
(c) Cursor to (90- 42.75) = 47.25 on Sine scale and read on C scale
224= side b
Case 3
Given a= 133, b= 156
To find Angle A and side c
Then 133 / SinA = 156 / sin B = c / 1
(a) Cursor to D133
(b) C156 to cursor
(c) Cursor to C10 and read on Tangent scale 40.45 = Angle A
(d) Cursor to 40.45 on Sine scale
(e) C133 to cursor and at D10 read on C the value 205 = side c
Alternatively
(a) C1 to D133
(b) Cursor to 156 on Reciprocal of C scale (giving 133 x (1/156) = 133
/ 156 ) and read on the tangent scale 40.45 = Angle A
(c) Cursor to 40.45 on Sine scale and read on Reciprocal of C scale 205
= side c
DIFFERENTIAL TRIGONOMETRICAL SCALES
The group of scales consists of the following:
Sine Differential scale (denoted by Sd) of a / SINa for Sine range 0 to 90°.
Tangent Differential scale (denoted by Td) of a / tana for Tangent range 0 to 60°.
Inverse Sine Differential scale (denoted by ISd) of x / sin-1x for inverse of
above Sine range
Inverse Tangent Differential scale (denoted by ITd) of x / Tan-1x for
inverse of above Tangent range.
The above four scales are positioned on the slide and together take up the equivalent of one 'scale length'. They are used in conjunction with C and D scales and are very simple to manipulate
The principle is as follows:
Since Sda = a / Sin a
Then a / Sda = a/ (a/sina) = a x (Sin a / a) = Sin a
Thus by setting the a value on D scale and dividing by Sda (i.e. the a value on the Sine Differential scale) the value of Sin a is read on D scale at C1(or C10)
e.g. To find Sin 43° Treat as 43 / (43/sin 43) i.e. 43 / Sd43
Cursor to D43
Bring 43° on the Sine Differential scale (i.e. Sd43
) to the cursor
At C10 read on D scale 0.682 = Sin 43°
e.g. To find Tan 36.5°
Cursor to D363
Bring 36.5° on the Tangent Differential scale (i.e. Td36.5)
to the cursor
At C10 read on D scale 0.740 = Tan 36.5°
e.g. To find the angle whose Sine is 0.66 (i.e. the value of Sin-10.66)
Treat as 0.66/ (0.66/sin-10.66) i.e. 0.66
/ ISd0.66
Cursor to D66
Bring 0.66 on Inverse Sine Differential scale (i.e. ISd0.66)
to the cursor
At C1on D scale read 41.3= Sin-10.66
Similarly the angle whose Tangent is 0.9 is found to be 42° by using the inverse Tangent Differential scale in conjunction with D scale
e.g. To find the value of 73 Sin 52°
Cursor to D52
Bring Sd52 to the cursor
Cursor to C73 and read on D scale at the cursor 57.5
It will be appreciated that the Direct Sine and Tangent Differential scales provide the necessary divisor correctives which, when applied to angle readings on D scale, give the respective trigonometrical functions on D at C1or C10. Similarly the Inverse Sine and Tangent Differential scales provide the divisor correctives which, when applied to function values on D scale, give the corresponding angles on D at C1 or C10
These Differential Trigonometrical scales give consistent maximum accuracy over the complete angle range and experience with them soon reveals their superiority compared with the orthodox Trigonometrical scales
The appearance of, for example, the Sine Differential Scale in the region of the 0° to 30° mark, in the respect that the distance is so comparatively short and the divisions so few, may suggest to the non-mathematical beginner that the accuracy is accordingly somewhat limited; but after a little practice with this scale, and thought regarding the nature of Sines, the user will correctly interpret the meaning of these small variations of the divisor correctives for the early angle range. Similar observations can be made with regard to the other scales. After comparison with tabulated and calculated results, users will soon realise that the highest significant figure accuracy possible by the C and D scales is consistently maintained by the Differential Scales over the complete angle range
On inspection of the Rule it will be observed that the Common Zero of the Direct Scales is at 'U' and coincides with the C scale reading 57.3, i.e. 180 / p. The Inverse Scales have their Common Zero at 'V which corresponds to a C scale reading of 0.01746 i.e. p /180.
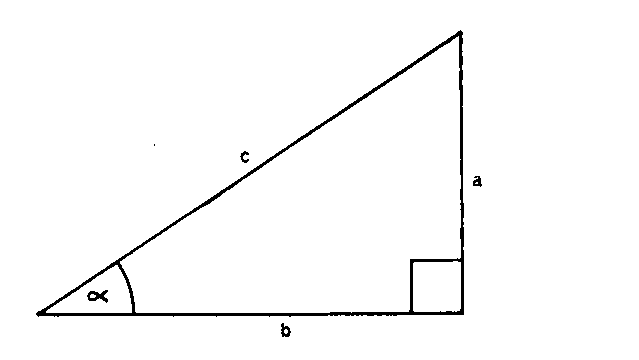
e.g. Given a = 160 and b = 231
To find Angle a
a / b = Tan a i.e. Tan-1 a/b = Tan-1 160/231
(a) Cursor to D160
(b) Bring C231 to the cursor
(c) Cursor to C10and read on D scale 0.6925 = a/b
(d) ITd6925 to cursor and read at C1on D scale 34.7° = a
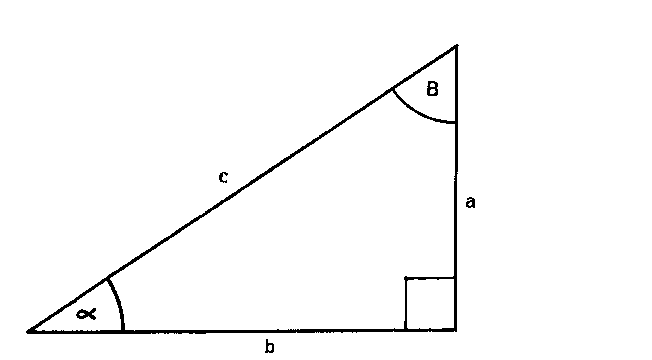
When given one side and an angle (other than the right angle) the following
relationship is useful:
a/a = b/Tda
= c/Sda
This is expressed diagrammatically by
Thus the remaining two sides are obtainable at a single setting of the slide (except where an 'end switch' is involved when a second movement of the slide is necessary).
e.g. Given c = 533, a=35.3°
To find a and b
Cursor to D533 and bring Sd35.3 in alignment.
Cursor to Td35.3 and read on D in alignment 435 = b
Cursor to C35.3 and read on D in alignment 308 = a
These are conversion constants on the C scale for use as divisors as follows:
U = 180/p = 57.2958 for Degrees to
Radians
V = p /180 = 0.01746 for Radians to
Degrees
m =(180 x 60) / p = 3437.75 for Minutes to
Radians
s = (180 x 60 x 60) / p = 206265.0 for
Seconds to Radians
Where:
a° is an angle expressed in Degrees
a' the angle expressed in Minutes
a" the angle expressed in Seconds
y the angle expressed in Radians
Then a° /U = a' /m = a" /s = y
Note: For particular advantages of the Differential Trigonometrical scales in Tacheometric Surveying see Appendix
Note: The following instructions cover models with three direct and three reciprocal Log Log scales. Thus only certain portions of the instructions relate to models with two direct log log scales.
The Log Log scales and Reciprocal Log Log scales are arranged on the stock and are used for calculations involving the exponential form.
Any positive number N may be expressed as a particular power P of any positive base B thus:
| N | = | BP |
| Hence Log N | = | P Log B |
| and Log Log N | = | Log P + Log Log B |
| or Log Log N - Log Log B | = | Log P |
i.e. the values B and N on the Log Log scale are separated by a distance representing Log P
e.g. Set cursor at 3 on LL3 scale and move slide bringing C1 to the cursor
Observe by cursor projection that
2 on C scale aligns with 9 on LL3
3 on C scale aligns with 27 on LL3
4 on C scale aligns with 81 on LL3
5 on C scale aligns with 243 on LL3
thus evaluating 32, 33, 34, 35
Similarly, on models with Reciprocal Log Log scales, by setting the cursor at .3 on the
LLo3 scale and bringing C1 to the cursor
2 on C scale aligns with .09 on LL03
3 on C scale aligns with .027 on LL03
4 on C scale aligns with .0081 on LL03
thus evaluating (.3)2, (.3)2, (.3)4
e.g. Evaluate N = 3.52.66
Cursor to 3.5 on LL3 scale
Bring C1 to the cursor
Move cursor to C266 and read on LL3 scale at the cursor 28.0= the value
of N
Cursor projection from Ll.1 to LL2 or LL2 to LL3 scales effects the process of raising to the 10th power (or vice versa extracting the 10th root)
Thus 3.5.266 = 1.395 the figure in alignment on the LL2 scale
When the base is less than unity the process is the same except that the Reciprocal Log Log scales are used
Thus 0.352.66= 0.0612
and 0.35.266= 0.7563
e.g. Evaluate (.35)2.66
(a) Cursor to .35 on LL03, C1 to cursor and then move cursor to C2.66. In alignment at
cursor read .0612 on the LL03 scale
(.35)2.66= 0.0612
(b) Read on the LL02 scale in the same alignment the value .7563
(.35).266 = .7563
Note: In order to decide which scale provides the value, mental approximation is necessary. It may be said that most students are more at ease with rough approximations of powers of quantities greater than unity than with those of quantities less than unity
For example, it is easier to mentally appreciate that
31/2 or Ö 3 »
1.7
33 = 27
than say
Ö.4or.41/2 ».63
(.4)3 = .064
Thus when dealing with the latter type as in the example it is useful to remember that at a particular setting on say the LL03 scale, the reciprocal of this value (greater than unity) appears in alignment on the related LL3 scale. The raising to the 'power' in question may then be observed on the greater than unity scales LL2 or LL3 and the final reading taken on the appropriate reciprocal log log scale.
The student should also observe in respect of reciprocals that those obtained by projections from LL2 to LL02 and vice versa are more accurate than those obtained by C, D or CI scales; but for the range covered by the LL3 and LL03 scales the advantage is with the primary scales C and D
To solve for P when N and B are known, i.e. to determine the log of N to base B
Proceed as in the following example:
e.g. (Base > unity)
Solve 5.3P = 92.0
Set the cursor at 5.3 on LL3 scale and move the slide so that C1or C10 (in this case
C1) is at the cursor. Move the cursor to 92.0 on the LL3 scale and read the significant
figures of P on the C scale at the cursor viz. 271
Then 532.71 = 92.0
or
log5.392 = 2.71
e.g. (Base less than unity)
.452P = .764
(Obviously the value of P is less than unity)
Set the cursor at .452 on the LL02 scale. Align C10 at the cursor and move the cursor to .764 on LL02. On C scale at the cursor read 339 the significant figures of P . . . decimal point considered .339.
To determine B when N and P are known
e.g. Determine B when B2.14= 40
Set the cursor at 40 on LL3 and move the slide so that 2.14 on C is in alignment. Transfer
the cursor to C1 and note the readings on LL2 and LL3 namely 1.188 and 5.6 respectively.
Mental approximation will immediately select 5.6 as the required value:
i.e. 5.62.14 = 40
and note that
1.18821.4 = 40
Note:
(i) That N and B are positions on the log log scales and their denominations must be
respected, inasmuch as values for 1.45, 14.5, 145 and 1450 are distinct positions at
different parts of the scales
(ii) That the significant figure value of P is employed on the C scale i.e. powers such as
.25 and 2.5 are identical on that scale: denominations, supported by mental
approximations, will dictate from which log log scale the N reading has to be taken
(iii) That 1 or 10 and P value on the C scale respectively align with B and N on the log
log scales.
(iv) That where roots occur they must be re-expressed as 'powers'
e.g. 3Ö as the .333 power
4Ö as
the .25 power
(v) Normally a negative base cannot be raised to a power e.g. (-5.94)3.41
cannot be evaluated: exceptions are where the 'power' is either an integer or the
reciprocal of an odd integer.
Where a power' and 'base' are such as to result in a value of N in excess of 2
x 104 as in the following
e.g. Evaluate 5.37.8
Take the 'power' in parts as 7.8 = 4 + 3.8
Evaluate 5.34 and 5.33.8 and obtain
5.34 = 790 5.33.8 = 565
Then 537.8 = 790 x 565 = 446000
When N is greater than 2 x 104, to determine P for a given B proceed
as follows
e.g. Determine P when 5.3P = 446000
Factorise 446000 as 1000 x 446
Then consider P = q + r where 5.3q = 1000 and 5.3r
= 446
Evaluate q and r and obtain q = 4.14 and r = 3.66
i.e. P= 4.14 + 3.66= 7.8
Logarithms to the base e or evaluation of eP
The log log scales are so positioned on the stock that projections therefrom on
to the D scale furnish the significant figures of logarithms to the base e.
Provisionally assign to the D scale the values 1.0 to 10 and remember that numbers in
alignment on the log log scales bear the relationship:
(LL2)10 = LL3
(LL02)10= LL03
Place the cursor at say 1.326 on the LL2 scale and note that the D scale reading in
alignment is 2.822.
Also observe reading on LL3 16.8
observe reading on LL02
.754
observe reading on LL03 .0595
It will be seen that
loge 1.326 = 0.2822 or e .2822 = 1.326
loge 16.8 = 2.822 or e 2.822 = 16.8
loge 0.754 = - 0.2822 or e -.2822 = 0.754
loge 0.0595 = - 2.822 or e-2.822 = 0.0595
The alignment of values is useful when evaluating hyperbolic functions since:
Sin hx= (ex - e-x) / 2
Cos hx = (ex + e-x) / 2
Tan hx= (ex - e-x) / (ex + e-x)
= Sin hx / Cos hx
In the case of x = 2.822 then
Sin hx = (16.8 - 0.0595)/2 = 8.37
Cos hx = (16.8 + 0.0595)/2 = 8.43
Tan hx = 8.37/8.43 = 0.993
(Note: The description of the use of the differential log log scales is not given in either of my copies of the Thornton instructions. The following is taken from a posting on the egroups slide rule forum by Cyril Catt, message number 418 of 4 February 1999.)
The Log Log Differential scales are used for amortisation and compound depreciation calculations. The top one is direct, the bottom one inverse.
For example, what will £1 amount to at 4 per cent compounded over 16 years?
A = (1+(r/100)) to the nth power = (1 + .04) to the 16th power
nx = 0.04 x 16 = 0.64
Set Y at 4 per cent and cursor at 64 on C
Find answer under cursor on LL1 = £1.873
Alternatively
Set index Y to per cent interest rate (4).
Set cursor to per cent interest rate on C (4)
Move the 1 (or 100) on the C scale to the cursor.
Move the cursor to the number of years (16) on the C scale.
Read answer under cursor on appropriate LL scale.
Another example. What rate of interest would raise an initial sum of £35 to £67.20
over 12 years?
67.20/35.00 = 1.92 (use C & D scales)
Then 1.92 = (1 + (r/100)) to the 12th power or (1 + (r/100)) = the 12th
root of 1.92
Set the cursor to 1.92 on the LL scale.
Move the slide to bring 12 on the C scale under the cursor.
Move the cursor to 1 (or 10) on the C scale - in this case to 1.
Move the slide so the Z index reads approximately the same on the
Inverse LL Differential Scale as the cursor on the D scale.
Read the required rate of interest, 5.59 per cent on the C scale under
the cursor.
The L constant at 2.3026 on C scale is useful for converting logs to base e to logs to base 10 since:
Log10N = LogeN/2.3026 =LogeN / L
The conversion is effected by bringing the L mark on C scale in alignment by cursor projection with the N value on the log log scale and reading the value of Log10N on D scale at C1 (or C10).
It will be realised that logarithms to any base can be obtained by making a mark on C scale in the position which aligns with the particular base on the log log scales (with C1and D1 in alignment of course) and by using the position marked on the C scale as a divisor for that base.
e.g. To find Log28
(a) With C1 and D1 in alignment move cursor to 2.0 on log log scale and
then make a pencil mark on C scale at the cursor position, namely 693
(b) Transfer cursor to 8 on log log scale
(c) Bring marked position at C693 to the cursor and read 3 on D scale
at C10
Then log28 = 3 (or 8 = 23)
Ps of Ö(1- s2) and Pt of Ö(1+t2)
With the Ps scale of Ö(1 - s2) it is possible, by cursor projection to the D scale, to obtain Cos a when Sin a is known or vice versa
The difference between two squares is treated as follows
x = Ö(c2- a2) = c Ö(1- (a/c)2 )
Since a/c = Sina = s
Then x = c Ö(1- s2)
e.g. Evaluate Ö(5.32 - 2.82 )
= 5.3Ö(1- (2.8/5.3)2)
(i) Cursor to D28, C53 to cursor and at C10 on D read 2.8
0.528 = 2.8/5.3
(ii) Cursor to .528 on Ps scale, C10 to cursor, cursor to C53 and read 45 on D scale
Then Ö(5.32 - 2.82
) = 4.5
Note: Where s is greater than 0.995 the form Ö2(1- s) may be used as a close approximation
The Pt scale of Ö(1 + t2) serves for
determination of the square root of the sum of two squares as under:
h= Ö(a2+b2) = bÖ(1+ (a/b)2)
Since a/b = Tan a = t
Then h=bÖ(1+t2)
e.g. Evaluate Ö(32 + 42 )
= 4Ö( 1+(3/4)2) = 4 Ö(1+(0.75)2)
(i) Cursor to 0.75 on Pt scale
(ii) Bring C1 to cursor
(iii) Cursor to Ca and read on D scale the value of h = 5
Single line cursors are supplied as standard since three line type cursors can be confusing. An exception to this however is the P221 Comprehensive model which has an additional line to the left of the centre line covering the A and B scales only and giving the 4 constant in relation to the centre line
The left hand line may be used for calculations involving areas of circles where diameter is given and vice versa and the distance between the left hand line and the main cursor line corresponds to the interval 0.7854 to 1 on the A scale
By setting the main line to a diameter on D scale the corresponding area of the circle can be read on A scale at the left hand line since passing from D to A scale squares the diameter and reading at the left hand line is the equivalent of multiplying on A scale by 0.7854= p / 4
The formula used is thus Area = (p /4 ) d2
It will be appreciated that area to diameter conversions may be made in the opposite
way
e.g. Given area of circle is 120 sq. ins
Find the diameter
(a) Set left hand cursor line to 1.2 on A scale
(b) From the main cursor line read on D scale 1236. Then diameter of
circle equals 12.36 inches
On the traditional type of three line cursor the right hand line covered horse power to kilowatt conversions, the distance between the main cursor line and the right hand line corresponding to the interval 0.746 to I on the A scale
e.g. Find the number of kilowatts in 150 hp
(a) Set right hand cursor line to 1.5 on A scale
(b) At the main cursor line read 112.
Then number of kilowatts equals 112
Appendix - Tacheometric Surveying
STADIA COMPUTATIONS
In the instructions for Differential Trigonometrical scales, reference was made to the
complete solution of the triangle given one side and one angle (other than the right
angle).
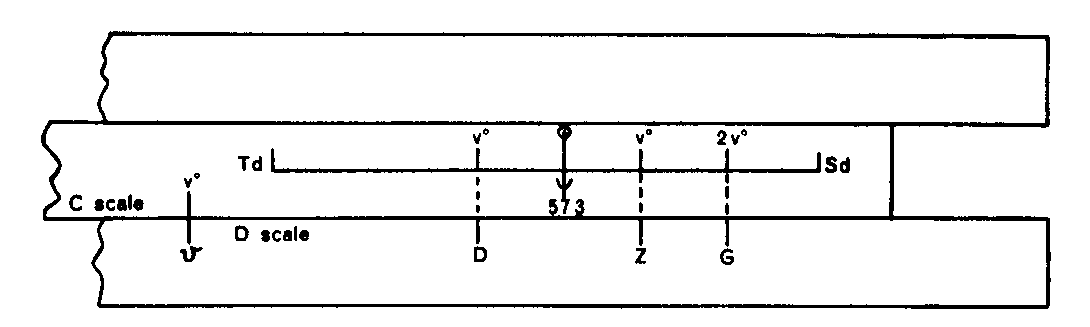
Since the computations of heights and distances from stadia data call for the treatment of two overlapping right angle triangles, it will be seen from the following that a rule which incorporates the differential Sine and Tangent scales provides the means of effecting the evaluation of D, v and Z (see figure) when G and V° are known, by a single setting of the slide (occasional end switching excepted).
In the following it is assumed that the tacheometric instrument used is provided with an analatic lens, also that the measurement staff is held in a vertical position
Where
V° = the inclination of the telescope
S = the (vertical) staff reading = AC
r = the 'corrected' (staff) reading = A1C1
D = the horizontal distance
v = the vertical distance
Z = Distance on Collimation Line
G = Uncorrected distance Z = k S
k = Constant for the wires (usually 100)
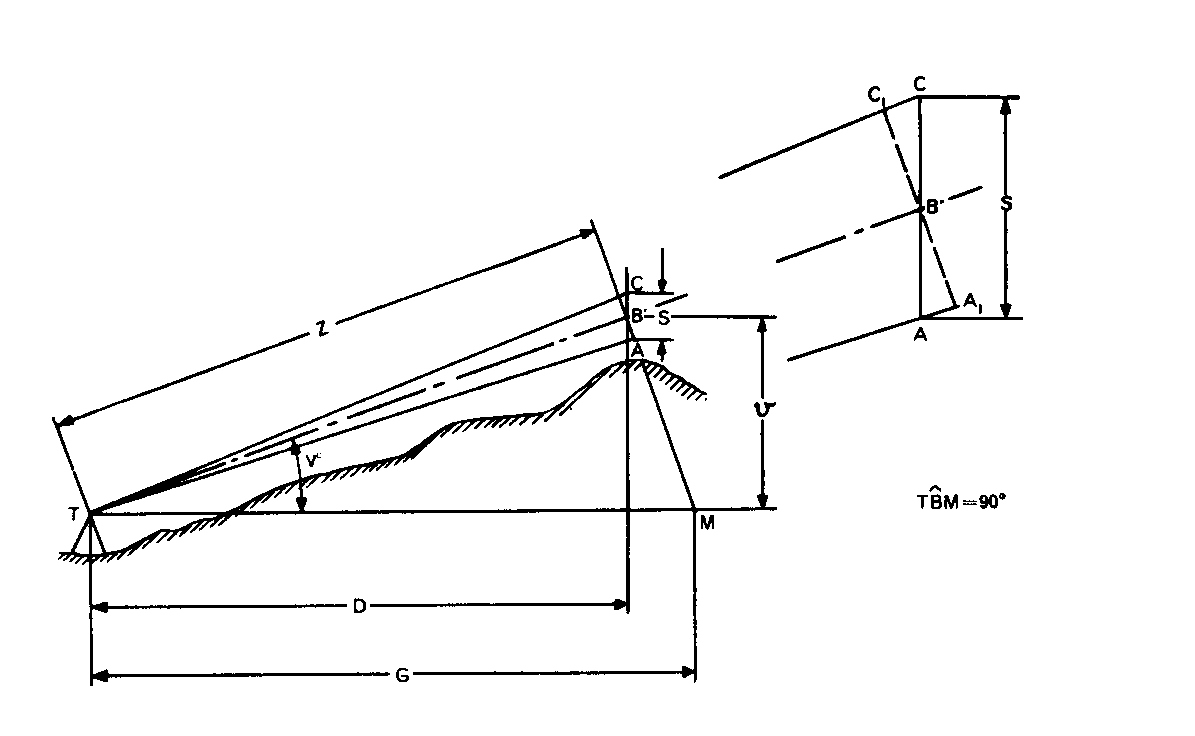
e.g. Determine D, v and Z, when S = 4.5 ft and V° = 200 and
the constant for the stadia lines = 100
G= 100 x 4.5= 450, V° = 20°, 2V° = 40°
Set the slide so that the 400 mark on the Sd scale aligns with 450 on the D scale
Then in alignment with:
20° on the Sd scale read the value of Z =
423 on the D scale
20° on the Td scale read the value of D =
397.4 on the D scale
20 on the C scale read the value of v= 144.6 on the D scale
That is, evaluate in accordance with the following diagram.
In the case of a value of G which occurs towards the left of the D scale such that Sd2V° when aligned with G results in Sdv°, Tdv° or Cv° being to the left of D1, then end switching must be effected by placing the cursor at C10 and then bringing C1 to the cursor. This will enable the values of the remaining projections on the D scale to be made.
The mathematical proof which substantiates the correctness of the foregoing method follows.
From the figure and remembering that
Sin V° Cos V° =
Sin 2V° / 2
we get:
v = G Sin V° Cos V°
= Tan V° G Cos2 V°
= D Tan V° = Z Sin V° = G Sin 2V° / 2
Then
V°/ v = V°/ (G
Sin V° Cos V°) = V° / (Tan V° G Cos2V°)
= V°/ D Tan V°
= V°/ Z Sin V°
= 2V° / (G Sin2V°)
V°/ v = (V° / (Tan V°)) / D = (V° / (Sin V°)) / Z =(2V° / (Sin 2V°)) / G
i.e.
V°/ v = Tdv°
/ D = Sdv° / Z = Sd2v°
/G = Sd2v° /(k s)
The slide rule interpretation of this form is given in the previous figure
When the angle V° is small (say less than 3°), then within the accuracy limits of measuring 'S'
(i) S » r
(ii) Z » l00r
(iii) D » Z
(iv) v » 100 r V°/
57.3
e.g. Given V° = 1° 14' (i.e.
less than 3°) and r = 6.17
To determine D and 'v'
Express 1° 14' as a degree and decimal =
1.233°
D » 100 x 6.17 = 617
To obtain 'v' evaluate
D V° / 57.3 = 617 x 1.233 / 57.3
Set cursor at D617, U (at C57.3) to cursor, cursor to 1.233
Read 'v' at cursor on D = 13.28 ft
(Note: This description relates specifically to all plastic Thornton slide rules. Do not follows these instructions for other types of slide rules.)
Removing the cursor
This is sometimes desirable for cleaning purposes and the procedure is as follows:-
SINGLE SIDED CURSOR
1 Move slide to one end of rule
2 Centralise the cursor
3 Compress the rule across its width in the region of the cursor which
can now be removed
DOUBLE SIDED CURSOR
1 Unscrew the four screws on one side of the cursor and note whether
cursor spring is at top or bottom (preferably the reverse side plate should be unscrewed)
2 Remove cursor plate and clean cursor as necessary
3 Replace the cursor with the cursor spring in correct position. Insert
the screws and tighten up sufficiently to hold the plate in position
4 Check that the black cursor line is square across the scales
(adjusting if necessary) and then tighten up slightly to secure the plate
Note: The double sided cursor may also be cleaned by sliding a piece of tissue paper under the plates as an alternative to removal
Cleaning the slide rule
The slide rule may be cleaned simply by washing it in a lukewarm solution of soap and water
Major historical developments in the evolution of the slide rule
| *1614 | Invention of logarithms by John Napier, Baron of Merchiston, Scotland | |
| *1617 | Development of logarithms 'to base 10' by Henry Briggs, Professor of Mathematics, Oxford University | |
| *1620 | Interpretation of logarithmic scale form by Edmund Gunter, Professor of Astronomy, London | |
| *1630 | Invention of slide rule by the Reverend William Oughtred, London | |
| *1657 | Development of the moving slide/fixed stock principle by Seth Partridge, Surveyor and Mathematician | |
| *1775 | Development of the slide rule cursor by John Robertson of the Royal Academy | |
| 1815 | Invention of the log log scale principle by P. M. Roget of France | |
| *1900 | Re-introduction of log log scales by Professor Perry, Royal College of Science, London | |
| *1933 | Differential trigonometrical and log log scales invented by Hubert Boardman, Radcliffe, Lancashire |
*denotes British development
| Return to | PIC 121 in collection |
| Thornton AD 050 in collection | |
| Thornton AD 060 in collection | |
| Calculations in A-to-Z | |
| Basics in A-to-Z |