| Slide rules HOME page | INSTRUCTIONS | CONTENTS |
SECTION ELEVEN
THE DUALISTIC RULE
Duplicated C & D Scales - Special 20" Scales for ordinary calculations - Squares and Square Roots - Cubes and Cube Roots - Log Log Scales.
IN Section 10 we examined the Electrical rule, which includes as part of its scale equipment duplicated C and D scales. We attempted to show that a saving of time can be effected when this type of rule is used. We explained that the c and d scales are identical with the C and D scales, but that the former are positioned so that the p in c is immediately over the 1 and 10 of C and the p in d over the 1 and 10 of D. This arrangement of scales enables the user to multiply or divide by p by merely projecting by means of the cursor index X from D to d or vice versa. We pointed out that a special 2-line Cursor is necessary if full advantage is to be taken of the duplicated scales.
We propose now to study a type of rule which, although closely resembling the Electrical rule in respect of the duplicated scales, is different in some respects.

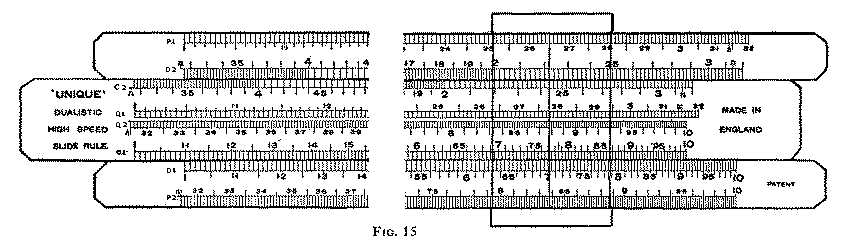
In this particular rule, shown in Fig. 15, the 1 of c is immediately above Ö10 in C, and similarly, the 1 of d is directly over Ö10 in D. Now Ö10 (which is exactly midway between 1 and 10 of any scale, as will be agreed if a little consideration is given to the logarithms of the numbers) has a value very near to 3·16 and thus is not far removed from p(= 3.14) so at first sight the two rules we are comparing may appear identical in the layout of their duplicated C and D scales.
The slight difference in the relative positions of the "folded" scales means that we cannot with the Dualistic rule multiply or divide by p by simple projection, but as a compensation, the 2-line cursor is not required for the comprehensive use of the Dualistic rule.
(The reader will readily appreciate that an additional broken line can easily be added to the cursor to provide the facility of multiplying and dividing by p, but we do not recommend such an addition. In any event, the point is of no great importance since the other features of the duplicated C and D scales are predominant.)
Apart from work of a specialised nature, probably 90% of the computations effected by slide rule involve the use of the C and D scales only. In the Dualistic rule these scales occupy their usual positions. They are designated by the symbols C1 and D1 and lie along the lower edge of the slide, and on the adjacent edge of the stock, respectively, as seen in Fig. 15
The upper margin of the slide, and the edge of the stock adjacent to it, are equipped with modified C and D scales. These are designated by C2 and D2 respectively, and are used in conjunction with the C1 and D1 scales, as described below.
The extreme margins of the stock and the centre of the slide are provided with a pair of 20" scales. These will be recognised as the principal scales of the 10/20 rule. They may be used separately; they are equivalent to a 20" rule and give the same high degree of accuracy. Scale references P1, P2, Q1 and Q2. These scales may be used in conjunction with the C1 and D1 scales, as will be demonstrated presently.
On the reverse of the slide three scales, LL1, LL2 and LL3, will be found; these are three sections of a continuous log-log scale, extending from 1.01 to 40,000, and are used with the slide inverted in conjunction with the D1 scale.
C1 and D1 Scales
As stated above, these are the C and D scales of the standard type slide rule. The instruction given in Section 4, dealing with the operations of multiplication and division, apply without modification, except that C and D should be read as C1 and D1 respectively. In all cases when a calculation involves the use of the C and D scales only, the standard slide rule, or the Dualistic rule, may be used without any discrimination.
C2 and D2 Scales
On inspection, it will at once be seen that these two scales are divided in the same manner as the C1 and D1 scales, but they are placed differently on the rule. The 1 of the scales C2 and D2 is in the middle of the length of the rule. The scales commence at p at the left-hand end of the rule; the readings increase, reaching 10 (or 1) at the mid-point, and then increase, reaching p at the right-hand extremity of the rule.
Scales C2 and D2 should not be used alone for multiplication and division. A few simple examples will at once show that, although multiplication or division may be effected with their aid, frequently the result is off the scale at the first setting, and cannot be obtained without traversing the slide through its own length. The same dilemma sometimes arises with the C1 and D1 scales when multiplying, but the traversing of the slide is rather more easily effected. In any case, there is no advantage gained by using C2 and D2 in preference to C1 and D1, and since all slide rule users are familiar with the C1 and D1 scales, it is advisable to adhere to them. To illustrate this point the reader is asked to compute 6 x 4 using C2 and D2 scales. On setting 1 C2 to 4 D2 it will be found that the 6 C2 lies beyond the D2 scale at the left-hand end. The result may be obtained by traversing the slide. Set the cursor index X to the p near the right-hand end of C2, and move the slide to bring the p at the left-hand end of C2 under X. Immediately above 6 C2 will be found the result, 24, in D2.
Scales C1, D1, C2 and D2 used in Conjunction
Computations involving multiplication and/or division are more rapidly effected when using these four scales than when C1 and D1 only are employed. The following example is designed to illustrate this feature:
Compute the value of (3·1 x 6·4 x 9·2) / (l·5 x 11·2)
Using C1 and D1 only, and performing division and
multiplication alternately since this saves time, the following operations are required:
To 31D1 set 15C1.
Set X to 1C1. 10C1 to X. X to 64C1.
112C1 to X. X to 1C1.
10C1 to X.
Result: 109 in D1 immediately under 92C1.
Approximation, performed mentally, shows the answer is of the order 10, and the result
therefore is 10·9.
Using the four scales:
To 31D1 set 15C1.
Set X to 64C2. 112C2 to X.
Result: 109 in D2 above 92C2.
If the rule is used to carry out these two series of operations, it will be found that by using all four scales the number of movements of slide and cursor is greatly reduced and the actual distances through which the slide and cursor are moved in these various operations are very much smaller. Greater accuracy will be attained, because in the course of time all slide rules develop small errors in their scales due to shrinkage or other distortion, and scales which originally were identical differ slightly in length. Critical inspection will almost invariably show that in slide rules which have been in use for some time, the overall lengths of scales on slide and stock differ slightly. With such a rule, imagine multiplication of 12 x 4 is being effected using C1 and D1 scales. Set 1C1 to 12D1 and the result, 48, appears in D1 under 4C1. If the slide scale has, through shrinkage, become, say, slightly shorter than the stock scale, a small error will be seen, the 4C1 falling just below the 48D1. Using the Dualistic rule, set 1C1 to 12D1, and read the result, 48, in D2 over 4C2. With this setting the length of slide scale used is only about 1", and the error will be only about one-sixth of that involved in using the C1 and D1 scales, where the length of slide employed is about 6". The same argument applies to any series of operations.
The principle involved in using the four scales of the Dualistic rule is the same as that employed in slide rules generally. Multiplication and division are effected by adding or subtracting logarithms, but with two sets of scales available there are alternative scale readings provided, and the manipulation of the rule is easier and speedier than in the case of the standard slide rule.
In using the Dualistic rule the first factor is selected in the D1 or D2 scales. The choice of scales is unrestricted, but it is an advantage to start with that scale in which the first factor lies near the middle of the length of the rule. If the first factor lies between 2 and 6, use the D1 scale, but if it lies between 6 and 2, start in the D2 scale. For the factors used subsequently there are alternative scale readings, and the one lying nearest should be used. An example will make this selection of factors clear.
Example: Evaluate 3 x 1·2 x 9/4 x 2.5.
Set 1C2 to 3D1 (using X). X to 12C2.
4C1 to X. X to 9C2. 1C2 to X. X to 25C1.
Result in D1 under X is 20·2.
It will at once be noticed that the movements of slide and cursor are small compared with those necessary if the C1 and D1 scales are used alone.
Whether the final result appears in D1 or D2 depends upon which scales, C1 or C2, were used for the intermediate factors; the determination presents no difficulty. Very often, especially in short computations, the order of the result is already known, and the slide rule is used to obtain an accurate figure. In such cases it is only necessary to glance at the results lying in D1 and D2 under X. These values differ in the ratio of Ö10 to 1, i.e. about 3·16 to 1. In such a case the appropriate reading will be obvious.
In longer computations, when the result is not obvious, a rough approximation should be made to determine the position of the decimal point. This approximation will also disclose in which of the two scales D1 or D2 the result lies.
The following method for determining in which scale the result lies may be preferred, and the reader is advised to spend a few minutes making himself familiar with it, since it applies also to the 20" scales which will be dealt with later. The method may, at first reading, sound complicated. It is, in fact, very easy of application and has earlier been explained in Section 9, but we think some repetition here may be desirable. We have in mind also the fact that an experienced slide rule user may be reading this section without having perused the earlier notes.
Every multiplication, or division, or combined multiplication and division, involves using two factors in the C scale. In a multiplication the 1 (or 10) C is set to some value in D, and the result found in D opposite the multiplying factor in C. In division the divisor in C is first set, and the result read opposite the 1 (or 10) C, and in multiplication/division, the divisor in C is set and the quotient obtained opposite another factor in C. In applying the method - which we believe to be original -it is only necessary to observe whether the two factors are both in the same C scale or whether one is in C1 and the other in C2. If the two factors are selected in different sections of the C scale, the result is obtained by crossing from D1 to D2, or vice versa; if both factors lie in the same part of the C scale, the result will be found in that part of the D scale in which the number being multiplied or divided appeared.
A simple example may assist. Suppose multiplication of 8 x 3 is desired. There are six different ways of obtaining the result, 24, they are:
| (a) | Set 1 C2 | to 8 D2 | Result in D2 | opposite 3 C2 |
| (b) | Set 1 C2 | to 8 D2 | Result in D1 | opposite 3 C1 |
| (c) | Set 10 C1 | to 8 D1 | Result in D1 | opposite 3 C1 |
| (d) | Set 10 C1 | to 8 D1 | Result in D2 | opposite 3 C2 |
| (e) | Set 1 C2 | to 8 D1 | Result in D2 | opposite 3 C1 |
| (f) | Set 10 C1 | to 8 D2 | Result in D1 | opposite 3 C2 |
the cursor index X being used in setting where necessary.
In the first and third settings of the slide the two factors 1 and 3 lie in the same section of the C scale, namely, both in C2 in the first, and both in C1 in the third method. In both the result lies in the section of the D scale in which the factor 8 was chosen. In the other four methods the factors 1 and 3 lie in opposite sections of the C scale, and the result is always in the opposite section of the D scale from that in which the first factor 8 was selected.
In the simple example just cited it is easy to determine in which part of the D scale the result will be found, but in a longer one it is advisable to record the various operations as now suggested. When the first slide setting is made, note which section of the D scale is used and jot down D1 or D2 as the case may be. If in the next operation the two factors used are in the same section of the C scale, take no further notice of them, but if they are in different sections of the C scale write a stroke thus, /, following the D1 or D2. Proceed in this way, making a stroke each time scale C1 and C2 are both used in any one setting of the slide, the second stroke cancelling the first by changing it into a x, so the record starting with, say D1, would next become D1/, and then D1 x. At the end of the computation the record will finish either with D1, or D1/, or D1 x. If the last symbol is a stroke, the final result will lie in the D2 scale; in other cases it will lie in D1.
Example: Evaluate (2·8 x 93 x 107 x 46) / (18 x 52 x 29).
| Set X to 28D1 | and jot down D1 |
| ,, 18C2 to X | } and jot down / |
| ,, X to 93C1 | |
| ,, 52C1 to X | } and jot down \ |
| ,, X to l07C2 | |
| ,, 29C1 to X | } No symbol necessary here. |
| ,, X to 46C1 |
Under X read 472 in D1, and 1495 in D2.
The symbols when written down in line result in D1 x ; the indication is that the result is in D1. Approximation gives 46 and the result is 47·2.
The scales lying along the top and bottom edges of the face of the stock designated by the symbols P1 and P2 respectively, together form a 20" logarithmic scale, and in combination with a similar pair of scales placed in the middle of the slide and designated by Q1 and Q2 form the equivalent of a 20" slide rule.
When a higher degree of accuracy than can be derived from the 10" C and D scales is desired, the P and Q scales should be used. Inspection of the illustration will show the additional dividing which has been made possible by the use of these long scales.
Multiplication and division are effected by using the P and Q scales and the cursor index X. The method given earlier for determining whether the final result should be read in D1 or D2 may be adopted when there is any doubt as to whether the result appears in P1 or P2. This method has already been dealt with fully and need not be repeated. Two examples are now given to illustrate the use of the 10/20 scales.
Example: Evaluate (13·65 x 23·4) / 39·6 .
Set X to 1365P1. 396Q2 to X. X to 234Q1.
Result is 807 in P2.
The value in P1 under X is 255 and it is obvious that this result is incorrect. 396 appeared in Q2 and 234 in Q1, therefore the result must be in P2, since the first factor, 1365, is in P1. It is quite unnecessary to write down the symbols, but if, for illustration only, we do so, they will be P1 /. The stroke at the end indicates the final result is in the opposite scale to that in which the first factor, 1365, was found: 13 into 39 is 3, and 3 into 24 gives 8 as an approximate result. Now, with two values under X, 807 and 255, there is no difficulty in selecting the correct one and at the same time inserting the decimal point. Result: 8·07.
A longer example is now given:
Evaluate (4·4 x 69·2 x 24·6 x 1·246 x 36) / (15·1 x 82.2 x 18·6 x 28·1).
| Set X to 44P2 | Note down P2 |
| 151Q1 to X | } and note down / |
| X to 692Q21 | |
| 822Q2 to X | } and note down \ |
| X to 246Q1 | |
| 186Q1 to X | } No symbol required here. |
| X to 1246Q1 | |
| 281Q1 to X | } and note down / |
| X to 10Q2 | |
| 1Q1 to X | } and note down \ |
| X to 36Q2 |
The symbols written in line should appear P2 x x, showing the result is in P2. It is 519.
Approximation. - 4·4 into l5 is slightly over 3, which divides into 69 about 20: 20 into 82, say, 4, 4 into 24 gives 6, 6 into 18 is 3, and 3 into 36 gives 12: 12 times 1·2 is 14 approximately and we are left with 14/28 = ·5 as the approximate result. The actual result is, therefore, ·519; it lies in P2, as indicated by the symbols.
The procedure explained in Section 4 for determination of position of decimal point, may be used if desired, but we strongly recommend the approximation method as being easier and safer. In a long computation there is a risk that a factor may be inadvertently omitted in the slide rule manipulation. The approximation if carefully made will disclose the error - another sound reason for making it.
The reader is now advised to practise the use of this new rule by working through a few simple examples, the results of which may easily be checked. It is confidently predicted that when familiarity with the scales is attained the rule will make an appeal as being superior to the standard type. The difficulties - if there are - have now been dealt with and the remaining instruction deals with simple points.
The relative positions of the 10" and 20" scales give a ready means of evaluating squares and square roots. The square of any number is obtained by projecting by means of X, the number from either Q1 or Q2 into C1. For example, 1·6, when projected from Q1 into C1, gives 2·56. When projecting from Q2 to C1, the squares are 10 times the actual values of the numbers engraved along the C1 scale. 5 in Q2 lies immediately above 2·5 in C1, and this value must be read as 25. Readers now familiar with the A, B, C and D scales of a standard rule will notice the similarity in procedure. They will also notice the higher degree of accuracy possible with the longer scales.
Square roots are obtained by the reverse process of projecting from C1 into Q1 or Q2. Square roots of numbers from 1 to 10 are obtained by projection from C1 into Q1, and square roots of numbers from 10 to 100 by projection from C1 into Q1. When a number whose square root is desired lies outside the range 1 to 100, the procedure outlined in Section 5 should be used, reading Q1 for the left-hand half of scale A, and Q2 for the right-hand half.
Scales P1, P2 and D1 may be used for squares and square roots if preferred; the procedure will be obvious from the instructions given above.
Cubes are easily obtained by setting the 1 (or 10) of C1 to the number in D1 the cube lies in D1 immediately below the number in Q1 or Q2. To cube 2·2 set 10C1 to 2·2D1 set X to 2·2Q1 and read in D1 under X the result, 10·65, the decimal point being inserted by inspection.
Cube roots are evaluated by setting X to the number in D1 and then moving the slide until the value in D1 coincident with 1 (or 10) C1 is the same as the number in Q1 or Q2 under X. Suppose the cube root of 2 is required. Set X over 2 in D1 now move the slide about an inch to the right of its mid- position, and then carefully adjust it until the value in D1 coincident with 1 C1 is the same as the value in Q1 under the cursor index X; this value will be found to be 1 ·26, which is the cube root of 2 (1.25992).
It may assist to observe that:
If the number lies within the range 1-10 its cube root will be found in
Q1 and coincident with 1 C1.
If the number lies within the range 10-31 (p3)
its cube root will be found in Q1 and coincident with 10C1.
If the number lies within the range 31-100 its cube root will be found
in Q2 and coincident with 1 C1.
If the number lies within the range 100-1000 its cube root will be
found in Q2 and coincident with 10C1.
Numbers from 1 to 1000 have cube roots from 1 to 10. If the number whose cube root is required is not within the range 1-1000 it should first be altered by moving the decimal point three, or multiples of three, places to right or left to bring the number within that range. The cube root should then be found as detailed above, and finally the decimal point of the result should be moved back one place for each step of three places made in the original number.
Example: Find the cube root of 116,300.
Moving the decimal point three places to the left alters the figure to
116·3, which lies within the 1 to 1000 range. The cube root of 116·3 is 4·88. The
decimal point must now be moved one place to the right, giving the actual result as 48·8.
In evaluating cube roots it is a good plan to find the nearest integral result mentally.
Example: Find the cube root of ·682. First move the decimal point three places to the right, so that the number becomes 682. The cube of 5 is 125, which is well below 682. Try the cube of 7; 7 x 7 = 49 (say 50); 7 x 50 = 350, still too small; try 9; 9 x 9 = 81; and 9 x 80 = 720. The required cube root is less than 9. Set X over 682D1 and the slide so that 10C1 is over 9D1. Now move the slide slowly to the left until the reading in D1 below 10C is the same as that in Q2 under X. These identical values are 8·8. The cube root of 682 is 8·8, and of ·682, ·88.
Squares, square roots, cube and cube roots, maybe evaluated easily with the aid of the log-log scales, often with a higher degree of accuracy than can be attained with the P and Q scales.
When the log-log scale is used the slide should be inverted so that the surface which generally is underneath is brought uppermost, or, if the log-log scale is fitted to a separate slide, the slides should be interchanged. The log-log scale provides a means of effecting unusual computations. Its most useful property is the ease with which powers and roots may be evaluated, even when the power root is a mixed number.
Suppose the value of 8·41.79 is required. Set 8·4LL3 to 1D1, then immediately above 1·79D1 will be found the result, 45·1, in LL3. If the index of the power is negative, e.g. 8·4-1.79, the value of 8·41·79 should first be evaluated and the reciprocal of this be found, using the C and D scales;
i.e. 8·4-1·79 = 1 /45·1 = ·0222.
To evaluate 4.15Ö1·31; to 415D1 set 1·31LL2, and then use X to project 10D1 into LL1 and read the result 1·067.
Results outside the range of the log-log scale may be obtained by the methods suggested in Section 6.
Logarithms to any base may be obtained by setting the base in LL to l of D1, or 1 of D2 and projecting the number whose log is required from the log-log scale into D1 or D2. The log so obtained will be complete, comprising characteristic and mantissa. Common logarithms are found by setting the l0LL3 to 1D1. It will be seen that immediately below 100LL3 stands 2D1, 2 being the log of 100. Below 1000 stands 3 and below 10,000 stands 4. To obtain the logs of numbers in LL1 and LL2 the cursor index must be used to project into D1. If the number whose log is required lies towards the left-hand end of the log-log scale, l0LL3 should be set to 10D1, or 1D2.
Natural logarithms are obtained by setting the value 2·7183 near the left-hand end of the LL3 scale to the 1 of D1. This setting will enable all the natural logs of numbers within the range of the log-log scale to be read without moving the slide; the numbers in LL1 and LL2 being projected into D1 by using the cursor index X.
It is useful to remember that the 10th powers of numbers in LL1 lie immediately below in LL2, and the 10th power of numbers in LL2 lie immediately below in LL3.
© Hodder Stoughton, reproduced with permission.
Return to
Dualistic rule in
Collection