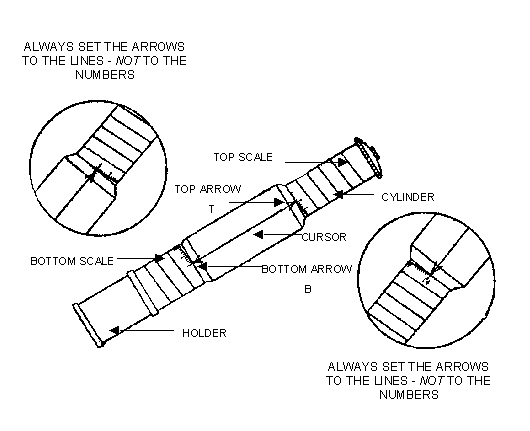
| Slide rules HOME page | INSTRUCTIONS | MANUALS | < SITE MAP > |
GENERAL DESCRIPTION.
The Calculator consists of three parts :-
1. THE HOLDER and 2. THE CYLINDER on which are mounted spiral logarithmic scales.
3. THE CURSOR (or Indicator), carrying at each end an engraved arrow, or pointer, which
can be set to any mark, or to which any mark can be set.

DETAILS OF SCALES.
Model K.
THE HOLDER carries a logarithmic scale 66 in. long, from 1 to 10, graduated as follows
:-
By .001 from 1 to 1.12
By .002 from 1.12 to 2
By .005 from 2 to 4.
By .01 from 4 to 10
In order that the range of the scale may be unlimited, decimal points are not marked. Thus the reading 212, for instance, also serves for 2120, 21200, 21.2, 2.12, etc., etc. The position of the decimal point in the answer is found by inspection or by the application of the rules given on pages 7 and 8.
THE CYLINDER carries two scales in series which are identical in all respects with the above. The point at which, these two scales meet half-way up the Cylinder is denoted by the word "ONE," and is referred to in the following pages as the "MIDDLE UNITY," or "UNITY."
Model L.
THE HOLDER SCALE on this Model is similar to the Holder Scale on Model K.
THE CYLINDER carries two scales, of which the upper one is identical with the Holder Scale, and operates with it for multiplication, division, &c. There being no MIDDLE UNITY on this scale, when calculations of this nature are performed on the Model L, the UNITY (one) at the top or bottom of the scale, as may be necessary, is used in its place.
The lower scale is graduated from 0 to 1, in 2,000 equal divisions of .0005 each. This is used in conjunction with the Holder Scale to give direct readings of the logarithm of any number, by means of which roots and powers are obtained.
METHOD OF OPERATION.
The following sequence of movements should always be adhered to in operating the Instrument :-
MOVEMENT 1. Take the HOLDER in the left hand, and open Instrument gently to full
extent. Move CURSOR to set bottom arrow.
MOVEMENT 2. Move CYLINDER so that number on scale is set to top arrow (not the arrow to
the number). Do not touch Cursor while moving Cylinder.
MOVEMENT 3. Move CURSOR to set either arrow as required - the companion arrow will then
point to the answer (see following examples)..
GENERAL RULES
The following abbreviations are used to render the descriptions more precise :-
B = Bottom Arrow or Pointer on Cursor.
T = Top arrow or Pointer on Cursor.
Unity = Middle Unity on Model K or Available Unity on Model L (see above).
To MULTIPLY
1. Set B to Multiplicand.
2. Set UNITY to T.
3. Move T to Multiplier.
4. Read Answer at B.
To DIVIDE.
1. Set B to Dividend.
2. Set Divisor to T.
3. Move T to UNITY.
4. Read Answer at B.
Problems of Proportion, Practice, Percentage, &c. involve either one, or a combination of both, of these operations.
EXAMPLES.
The following instructions apply to both Models K and L.
Multiplication.
Multiply 115 by 23.
Set B to 115. Set UNITY to T. Move T to 23. Read answer at
B: 115x23=2645.
Division.
Divide 833 by 17.
Set B to 833. Set 17 to T. Move T to UNITY. Read
answer at B: 833/17=49.
Combined Multiplication and Division.
Solve (6 x 4 x 9) / (7 x 5 x 2)
Set B to 6. Set 7 to T. Move T to 4.
(B now indicates answer to 6 x 4 /7 )
Set 5 to T. Move T to 9.
(B now indicates answer to (6 x 4 x 9) / (7 x 5) )
Set 2 to T. Move T to UNITY. Read answer at B: 3.086.
Proportion.
I. Solve 12 : 7 :: 16 : x ?
Set B to 12. Set 7 to T. Move B to 16. Read answer at T. 12 : 7 ::
16 : 9.333.
II. Solve 18 : 4 :: x : 53 ?
Set B to 18. Set 4 to T. Move T to 53. Read answer at B. 18 : 4 :: 238.5
: 53.
III. Divide 8975 in the proportions 83 : 79 : 33 :19.
Set B to 8975. Set sum of required proportions, viz., 214, to T. Without
altering the setting of the Instrument, move T in succession to 83, 79, 33, 19, and read
the corresponding proportions at B, viz., 3481, 3313, 1384 and 797. (On Model L this
calculation necessitates "closing in" the Cylinder. See below.)
Percentages.
I. What is 5% (a) of 162 ?
(b) off 162 ?
(c) on 162 ?
Set B to 162 (capital amount or quantity). Set UNITY to T. The Instrument is
now set to solve percentage problems involving % OF, % OFF and % ON 162.
(a) Move T to 5 (rate %). Read answer at B: 5% of 162=8.1.
(b) Move T to 95 (100-rate %). Read answer at B: 5% off 162=153.9.
(c) Move T to 105 (100+rate %). Read answer at B: 5% on 162=170.1.
II.What % of 3735 is 4.54 ?
Set B to 3735. Set UNITY to T. Move B to 4.54 Read answer at T: .12155%.
III. What is the percentage of profit on cost where goods purchased for £5,760 are
sold for £9,420 ?
Set B to 5760 (capital). Set UNITY to T. Move B to 9420 (selling price).
Read answer at T: 163.5. Percentage of profit=63.5% (163.5-100).
Constant Factors.
I. In cases where one pair of factors is repeated throughout a series of problems,
the Instrument may be set to the constant terms, and the answers found by subsequent
movement of the Cursor only.
In Percentage Example I, for instance, the Instrument being set to the constant terms 162: 100%, any percentage of, off or on 162 will be shown at B when T is moved to the relative figure, e.g., Move T to 45. Read answer at B: 45% of l62=72.9. Move T to 126. Read answer at B: 26% on 162=204.1, and so on.
II. Decimalise 3/32, 7/32, 15/32, 29/32.
Set B to 32. Set UNITY to T (32 and 1 being the constants in this series).
Move B in succession to 3, 7, 15, 29 and read corresponding answers at T, viz., .09375,
.21875, .46875, .9062.
Sterling Calculations.
The Sterling items must be reckoned as decimals of pounds, shillings or pence as best
suits the problem.
I. If 54 articles cost £39 4s. 6d., what is the price of 15 ?
(a) Set B to (£) 39.225. Set 54 to T. (The cost of any number of articles at this price can now be obtained by moving T to the number required.) Move T to 15. Read answer at B: 15 articles cost £10.895, i.e., £10 17s. 11d.
Alternatively :-
(b) Set B to 784.5 (shillings). Set 54 to T. Move T to 15. Read answer at B: 15 articles cost 217.9 shillings, i.e., £10 17s. 11d.
II. Find Interest on £675 at 61/2% p.a. for 29 days.
£675 x (6.5/100) x (29/365)
Set B to 675. Set UNITY to T. Move T to 6.5. Set 365 to T. Move T to 29.
Read answer at B: £3.486, i.e. £3 9s. 8<small> 3/4 </small>d. (If
preferred, multiply further by 240, and read answer at B: 836.75 pence i.e. £3 9s. 83/4
d.
In some calculations it may be found preferable to invert the setting of the Instrument and to work to the Unities on the Holder Scale instead of to those on the Cylinder Scale. In this case, the answer is of course read at the Pointer opposite to the one indicated in the foregoing examples.
Model L.
THE UPPER CYLINDER SCALE.- When this Scale is used in conjunction with the Holder Scale to perform the types of Calculations described in the preceding pages, it will be noted that upon occasion the Cylinder becomes closed in or opened out too far for the Pointer on the Cursor to be moved to the required figure. In this case proceed as follows, without altering the setting of the Instrument :-
To CLOSE CYLINDER IN. Move T to bottom UNITY.Set top UNITY to T.
To OPEN CYLINDER OUT.Move T to top UNITY.Set bottom UNITY to T.
The Pointer can then be set to the required figure and the calculation completed. This operation may be performed during any calculation and does not affect the process or answer in any way.
THE LOWER CYLINDER SCALE.- Where involved expressions occur above or below the line, the Otis King's Calculators offer valuable advantages over the ordinary slide rule, which, even if engraved with log-log scales, cannot solve the following, whereas Model L will give all powers and roots, fractional or otherwise, of all numbers without limit, and solve any expression, however extended. The following expression is given as an example :-
(1.0083.1 x 3Ö(63) x 4000 ) / (6 x 5Ö(260000) x 421.82 ) = 0.2495
All involved expressions must be replaced by their numerical value before the problem can be dealt with, and this prior process is, of course, common to both the slide rule and the Otis King's Calculator. The intermediate stage in dealing with the above problem is to simplify it into the following :-
(1.025 x 3.98 x 4000) / (6 x 12.11 x 900.1)
The process for effecting this is as follows :-
To LOGARIZE - (i.e., find the logarithm representing a number).
Set B to bottom UNITY of Holder Scale. Set ".000" of lower Cylinder Scale
to T. Move B to number (antilogarithm), and read mantissa at T.
To DELOGARIZE - (i.e., to find the number represented by a logarithm).
Set B to bottom UNITY of Holder Scale. Set ".000" of lower Cylinder Scale
to T. Move T to mantissa. Read antilogarithm (number) at B.
To ascertain any Power or Root of any number.
POWERS.
Multiply the logarithm of the number by the index of the power and take the antilogarithm
of the product
Example :- What is 1.0083.1
Log. of 1.008=0.0035.
0.0035x3.1=0.01085.
Antilog. of 0.01085=1.025.
Therefore 1.0083.1=1.025.
ROOTS.
Divide the logarithm of the number by the index of the root and take the antilogarithm of
the quotient.
Example :- What is 3Ö(63)
Log. of 63=1.7993.
1.7993/3=0.5998.
Antilog. of 0.5998=3.98.
Therefore 3Ö(63) =3.98
TO DETERMINE POSITION OF DECIMAL POINT.
The following rules apply to both Models K and L :-
A number having n figures to the left of the decimal point shall be designated as having +n places. A decimal number having n cyphers to the right of the decimal point, between the decimal point and any number other than 0, shall be designated as having -n places.
Thus the number:
5430000, has +7 places
674, +3,
81.2,+2,
7.82,+1,
0.45,+0,
0.0421,-1,
0.00675,-2
Multiplication.
To find the number of places (p) in the product (P = X x Y).
Let X have m places, and Y have n places.
RULE I. p=m+n or p=m+n-1.
(a) When the result is below the original setting p = m + n.
Example: 3 x 4 (m = 1; n = 1).
Set B to 3. Set UNITY to T. Move T to 4 (This is below setting.)
So, p = m + n = 2. Answer = 12.
(b) When the result is above the setting, the product has m+n-1 places
Example: 3 x 3 (m = 1; n = 1).
Set B to 3. Set UNITY to T. Move T to 3. (This is above setting.)
So, p = m + n - 1 = 1. Answer = 9.
Division.
To find the number of places (q) in the quotient (Q=X/Y).
RULE II. q = m-n or q=m-n+1 as follows :-
(c) When the result is above the setting, the quotient has m-n places.
Example: 3 ÷ 4 (m = 1; n = 1).
Set B to 3. Set 4 to T. Move T to UNITY. (This is above setting.)
So, q = m - n = 0. Answer = 0.75.
(d) When the result is below the setting, the quotient has m-n+1 places.
Example: 5÷4 (m=1; n=1).
Set B to 5. Set 4 to T. Move T to UNITY. Read answer at B. (This is below setting.)
So, q=1-1+1=+1. Answer=1.25.
Calculations involving Multiplication and Division.
RULE III. Two methods may be used in working out complex problems involving both multiplication and division. They are :-
(1) Taking numerator and denominator alternately.
(2)Taking all the numerators first and then dividing consecutively by the denominators.
Of these two methods, only the latter can be used if the position of the decimal point is required. If the other is used, the decimal point must be found by inspection.
First multiply consecutively the series of factors in the numerator and then divide consecutively by the factors of the denominator.
Take the algebraic sum of the places in the factors of the denominator from the algebraic sum of the places in the factors of the numerator, and to this result add the algebraic sum of the results obtained from the application of Rules I and II to the several steps of the problem.
Example: (432 x 32.4 x 0.0217 x 0.98) / (0.00000621 x 412000 x 0.175 x 4.71) = 141.14
| No. of places in factors of numerator | = 3 + 2 + (-1) + 0 | = +4. |
| No. of places in factors of denominator | = -5 + 6 + 0 + 1 | = +2. |
| Difference | = + 2. | |
| Results of various steps in calculation | = -1 +1 +1 | = +1. |
| Number of places in answer | = +3. | |
| Answer | = 141.14. |
| Return to | Otis King in non-standard rule in collection |