| Slide rules HOME page | INSTRUCTIONS | MANUALS | < SITE MAP > |
| Slide rules HOME page | INSTRUCTIONS | A-to-Z |
FOWLER'S LONG-SCALE CALCULATOR
VEST POCKET MODEL(RX)
For Engineers, Draughtsman and Science Students
(Supplied Complete in Leather Case)

Fowler's Calculators, like all Slide Rules, are based on the properties of logarithms, which enable Multiplication to be performed by addition and Division by subtraction. These operations are made mechanical by moving circular scales with logarithmic distances marked on them, which can added or subtracted from one another.
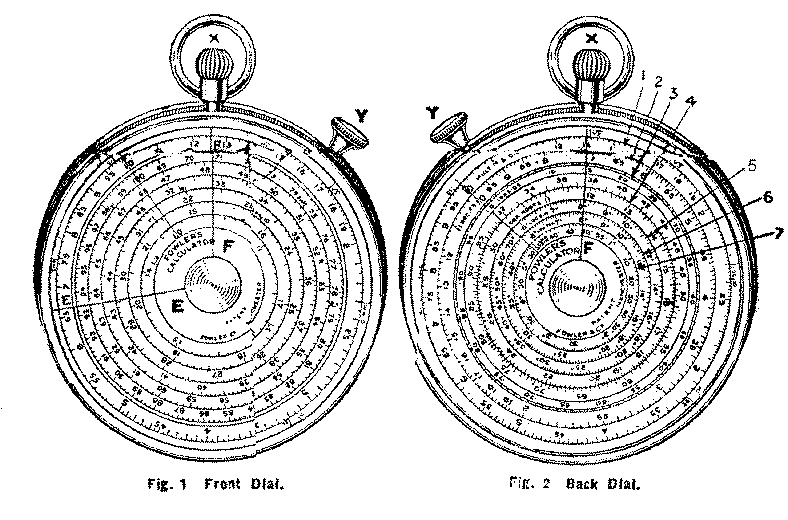
The instruments are all of standard size and price, and consist of a circular nickel case fitted at front and back with a glass cover. Within the case are two rotating metal dials 2 3/8 ins. diameter (see Figs1 and 2) on which the engraved scales are printed. These scales are operated by thumb nuts outside the case.
On each cover glass there is a fixed radial datum line. The front dial is also provided with a rotating radial line or Cursor.
No cursor is fitted to the back dial.
The instrument is contained in a separate velvet-lined nickel protecting case.
Every detail is made in our own factory by the aid of special machinery to secure the greatest accuracy and excellence of workmanship.
Features of Fowler's Calculators
Dials Synchronised.- The instruments are so constructed that when the zero line of front dial is set under Front Datum line, the Front Cursor line and Back Datum line aligns with the similar readings of outer scale. This is sometimes convenient for directly transferring values of functions from Back dial to Front dial, and is especially handy for determining Cube Roots.
Accuracy of results.-With the "Short-scale" of the front dial calculations of all kinds can be made rapidly and accurately to two and frequently three significant figures. If greater accuracy is required, the "Long-scale" can be used, which will give results accurate to three and often four significant figures.
Advantages over straight slide rules. Scales always clean. No slides to stick or become slack. No switching of slide; quicker to set. Results more accurate. Instrument fits in waistcoat pocket, and not affected by temperature, dirt or moisture.
The makers recommend the "Long-scale" type of instrument (here illustrated) to Engineers, Draughtsman and Science Students for all-round purposes as the most comprehensive and accurate pocket calculator ever made. Other special types are more convenient for special purposes, and descriptive circulars of these would be sent free on application.
DESCRIPTION OF DIALS
of Fowler's "Long-scale" calculator
The Front Dial, Fig.1,comprises an outer "Short-scale" complete in a single circle 6-7" in circumference, which can be used for Multiplication and Division in the same way as other types of Fowler's calculators.
The six inner circles form a similar continuous "Long-scale" 30" in total circumference. It is used just like a single circle or "Short-scale", though the "Short-scale"is sometimes convenient for finding an approximate result to determine the precise circle of the "Long-scale" on which to read the very accurate result.
Whether to use the "Short-scale" or the "Long-scale" is entirely in the choice of the operator according to his convenience and a degree of accuracy required.
The Back Dial, Fig. 2,comprises seven scales, reckoning inwards as follows:-
No. 1-A scale similar to the multiplying and dividing scales on the front dial.
No. 2-A scale of Reciprocals exactly similar to scale number one, but graduated contra clockwise instead of clockwise.
No. 3-A scale of Logarithms graduated at intervals of .01.
No. 4-A scale of Square roots from 0 to 100. (The values of the squares are read from scale number one). This scale extends continuously around the circumference.
No. 5-A scale of Log. Sine values from 5° 45' to 90°
From 5° 45' to 8° graduations every 5'
8° to 12° graduations every 10'
12° to 30° graduations every 20'
30° to 60° graduations every 1°
60° to 80° graduations every 2°
No 6-A scale of Log. Tangent values from 5° 45' to 45°
From 5° 45' to 8° graduations every 5'
8° to 12° graduations every 10'
12° to 30° graduations every 20'
30° to 45° graduations every 30'
No 7-A scale of Log. Sines from 35' to 5° 45'
From 35' to 1° graduations every 1'
1° to 3° graduations every 2'
3° to 5° 45' graduations every 5'
Note.-The values of the functions given on scales No. 3 to No. 7 can be read directly on scale No. 1 by means of the datum line or the inverse values by reading on scale No. 2.
Gauge points.-For facility in setting, both "Short-scale" and "Long-scale" of the front dial as well as outer scale of the back dial have the following values specially indicated:- Ö 2; Ö 3; loge 10; p ; gE(gravity English); E.H.P.(electrical horsepower); p /4; gF(gravity French)
Operating nuts.-The thumb nut X, Fig. 1. Operates the front dial only.
The thumb nut Y, Fig. 1,operates the cursor E of the front dial and also the back dial.
HINTS ON USE OF CALCULATOR
Use of scales.-All the scales of the dials are logarithmic and as the distance of the figures 1,2,3,4 ... 10 gradually diminish so does the legibility of each division and consequent accuracy of reading. Hence the advantages of a "Long-scale" over a "Short-scale".
Readings and settings of subdivisions depend entirely on the judgement of the observer, and in estimating fraction of values the difference between logarithmic distance and actual distance should be noted. Thus for calculation .25 is more than a quarter and .5 more than half way.
Any value may be assigned to the figures of the Scales, but proportionate values must then be accorded to the subdivisions. Thus 6 may also stand for .6, .06, .006, 60, 600, etc., but if taken, say, to represent 60, the subdivisions would then represent 61, 62, etc. and similarly for any other value accorded to the prime number.
Selection of proper units of measurement.-In making calculations by whatever method or instrument, care should be taken to express the quantities in proper units.
If an area is desired in square feet as the product of linear dimensions, these should be expressed in feet. If desired in square yards the dimension should be in yards.
It does occasionally happen that some dimensions are in one unit and others in a different unit. For example, in formulae for beams, breadth and depth are usually expressed in inches, and span in feet. Again, the weights of bars are generally given per foot run, although the sectional dimensions are in inches. Mistakes occur through overlooking these points.
Simplifying decimals.-In simplifying decimals values regard should be paid to the value of any terminal figures that may be struck off.
For example, if we wish to contract a value such as 15.647, then 15.65 is a nearer approximation than 15.64, because the figure 7 is nearer to 10 than 1. If the last figure had been 2 instead of 7, then 15.64 would have been more approximate than 15.65.
If the repeating decimal is less than 5,write it twice and increase the last figure by one. Thus 6.22 become 6.23.
If the repeating decimal is greater than 5, it need only be given once, but increased one in value. Thus 6.77 may be written 6.8.
A misconception of the fractional value of decimals sometimes causes mistakes, especially if there are cyphers to the right to the decimal point.
To avoid confusion, remember that when expressed as a fraction the number of cyphers in the denominator is the same as the number of figures after the decimal point. For example
3.04 = 3 + 4/100 = 304/100; 0.96 = 96/100; .002 = 2/1000
Fixing decimal points by mental calculation.-When possible, put all calculations in a simple fractional form. The correct position of the decimal place in the answer can be best determined by rapid mental multiplication and division. There are rules for doing this, but they are more trouble to remember then they are worth, and liable to cause mistakes. It is much better for the operator to depend on first principles and a little mental arithmetic.
For example, suppose value of following required:-
6.92 x 746 x 19.2 x 9
2876 x 92.5
We could reason mentally as follows:-6.9 is practically seven, and seven into 2876 is roughly 400; 400 into 746 is roughly two; 2 into 92.5 is roughly 45. This would be in the denominator, and for the numerator we still have left 19.2 times 9, roughly 170. This divided by 45 would obviously give a value less than 10. In putting down the answer, therefore, we should write all the figures after the first one to the right to the decimal point. A rough estimate like this occupies less time to make than to describe, and is safer than any cut and dried rule.
ARITHMETICAL EXAMPLES.
Multiplication.-Front dial. Either the "Short-scale"or the "Long-scale" may be used, but for purpose of illustrating the principle, the descriptions will be first confined to the single outer circle or "Short-scale" No.1.
Suppose the factors are a x b x c etc.
Set a under datum F by nut X.
Set cursor E at 1.0 by nut Y.
Set dial by nut X till b is under cursor E.
Read a x b under datum F.
If there is a third factor c:
Set cursor again at 1.0 by nut Y.
Set dial by nut X till c is under cursor E.
Read a x b x c under datum F,
and so on for any number of factors.
The calculation is similar using the other circles of the Front dial but the setting is precisely the same as described but as for the "Short-scale," but factors a, b, c, etc. are, of course, read exclusively from the "Long-scale".
In reading the answer, the first figure of the result, and hence, the particular circle on which to look for it, may be determined either by a preliminary working on the "Short-scale", or by rapid mental estimation as indicated under "Hints on the Use of Calculator". The value of the first figure of the answer, and whether it represents units, hundreds, thousands, etc. determines the position of the decimal point and the reading of the following figures of the answer from the subdivisions of the scale.
Division: Fractions:-If division is of simple form a/m use scale no. 1.
Set a under datum F by nut X.
Set cursor E to m by nut Y.
Set dial by nut X till 1.0 is under cursor.
Read a/m under datum F.
If division is of form a x b / m proceed thus:-
Set a under datum F by nut X.
Set cursor E to m by nut Y.
Set dial by nut X till b is under cursor E.
Read answer under datum F.
The numerator of the fraction must contain one more factor than the denominator. If there are not enough multipliers or divisors in the fraction, insert the figure 1 as often as required, e.g.:-
Operate a x b x c
as a x b x c
m
m x 1
Operate a x b
as a
x b x 1
m x n
m x n
The position of the decimal point in a calculation, if one as required, is found as explained above, either by inspection or rapid mental calculation.
Note The datum F is used only for first
multiplier and answer.
The dial is turned only for multipliers.
The cursor E is turned only for divisors.
Instead of operating as described, a complete fraction, may, of course, be worked by multiplying all the figures of the numerator and dividing this product by the product of all the figures of the denominator. The choice is a matter for the operator.
Squares and square roots.-These are given by a single setting of the back dial and reading directly with the datum from the Scale No. 1 to Scale No. 4, or vice versa. The numbers on scale No. 4 are the square roots of those on scale No. 1.
In fixing magnitude of square of a number, remember that:-
Square of any number between 1 and 10 lies between 1 and 100.
Square of any number between 10 and 100 lies between 100 and 10,000.
Square of any number less than unity is less than the number.
Square root of any number less than unity is greater than the number.
For example:-
(1/10)2= 1/100 : (3/7)2 = 9/49 ; Ö 64 = 8 ; 1/Ö (100) = 1/10
Rule.-If the number has an odd number of digits, read the square root on the smaller circle of square roots scale.
If the number has an even number of digits, read root on the larger circle of square root scale.
Cubes, Cube Roots, Nth powers, Nth roots.- If the calculator happens
to be fitted with a Cube Root back dial, instead of the one shown in Fig. 2, the values of
cubes and cube roots can be read directly at one setting, as explained in the case of
squares and square roots. Remembering that:-
Cube of any number between 1 and 10 lies between 1 and 1000.
Cube of any number between 10 and 1000 lies between 1,000 and
1,000,000.
Cube of any number less than unity is less than the number.
Cube root of any number less than unity is greater than the number.
(1/10)3 = 1/1000 ; 3 Ö (1/27) = 1/3
If the Calculator is not fitted with a Cube Root back dial, the cube root value can be obtained like that of the Nth root (where N may be whole or fractional) by means of logarithms from the following relation:-
If A is a number and x = An
Then x = n x log A
The fact that the front and back dials of the "Long-scale" calculator are synchronised and that the "Long-scale" extends over 6 circles, enables cube roots to be got by direct reading because.
3 Öx = 6 Ö (x2)
For example, let x be the number whose cube root is required.
First: Set zero-line on front ("Long-scale") dial, under
datum line on cover glass.
Second: Set number x on square root scale of back dial under
Datum line, then the reading under datum on outer scale of back dial is x2;
so also is the reading on outer scale of front dial under Cursor line, and the sixth root
of this number i.e..
3 Öx
is on one of the six circles of the "Long-scale" of front dial.
The precise circle is easily determined by bearing in mind the 103 = 1,000,
203 = 8,000, 303 = 27,000, 403 = 64,000 etc. and that for
any number.
Between 1 and
1,000 the cube root is between 1
and 10
"
1,000 "
8,000
"
10
" 20
"
8,000 "
27,000
"
20
" 30
"
27,000 "
64,000
"
30 " 40
etc.
etc.
Thus the finding of the circle on which to read the result presents no difficulty.
Logarithms.- The characteristic of a log, is the part to the left of the decimal point. It may be positive or negative.
The mantissa of a log, is the part to the right to the decimal point, and it is always positive. When multiplying or dividing for powers or roots, these points must be born in mind.
The characteristic of the log, if positive, is one less than number of figures to left of decimal point; if negative, one more than number of cyphers to right of decimal point.
Example:-Find log of 2675.
Set cursor to 2675 on Scale 1. Read mantissa of log, viz. 427 on log
scale. The characteristic of the log is 3 and the log of 2675 = 3.427
Example:-Find log of 50.75
Set cursor to 5075 on Scale 1. Read mantissa of log, viz. 7055 on log
scale. The characteristic in this case is 1 and the log of 50.75=1.7055.
The mantissa part of the log of a given number is independent of the position of the
decimal point, but the characteristic changes if the decimal point changes position,
e.g.:-
Log. 290 is 2.4624 Log. .29
is 1.4624
Log. 29.0 is 1.4624 Log. .029
is 2.4624
Log. 2.9 is 0.4624 Log.
.0029 is 3.4624
Logarithms are very convenient for finding powers and roots of numbers. See Nth Powers and Roots.
Reciprocal scale.-Scale 2 of the back of the dial affords a very convenient way of obtaining values as:-
1/a 1/a2 1/Öa 1/ (sin a) 1/(cos a) 1/(tan a) etc.
by simply setting the Datum line over these respective values and reading the corresponding values on Scale No. 2. It will be noted further that with these two scales the decimal value of any fraction having 1 as a numerator and any number as a denominator, can be instantly read. It matters not which scale is taken to represent the denominators, the other scale gives the decimal value. The product of any two opposed numbers on scales No. 1 and No.2 is, of course, equal to unity.
Percentages.-in the expression of percentages, attention should be paid to the basis on which it is measured. For instance, if A's salary is £75 and B's is £50, is would be true to say that A's salary was 50 per cent greater than B's, taking B's salary as 100 per cent. and equally true to say that B's salary was 33 1/3 per cent less than A's taking A's salary as 100 per cent. The fact is only expressed in two different ways. There can be no misapprehension in any case if the quantity representing the 100 is made clear. Set the question as a problem of fractions thus:-
Example:- In an examination, 27 scholars pass 1st. class, 35, 2nd. Class and 63, 3rd class. Express the various numbers as percentages.
The total number of scholars is 27 + 35 + 63 = 125.
If x, y, z are the three percentages, we have the following relationship:-
27/125 = x/100 and x
= 100 x 27 / 125 = 21.6 per cent.
35/125 = y/100 and y
= 100 x 35 / 125 = 28 per cent.
63/125 = z/100 and z
= 100 x 63 / 125 = 50.4 per cent.
For this class of question the instrument is very convenient. The fraction 100 / 125 occurs in each, and by setting 1.0 under the datum line and cursor F to 125, i.e. 12.5 on scale 1, the several percentages can be read off at the Datum line F by rotating the dial until the several figures 27, 35, 63, on scale 1, come under cursor E.
Proportion:- Set the question in fractional form,
a/b = x/c
Where x is the unknown, and may be the numerator or the denominator, as the operator finds convenient in setting the sum for solution. Hence by cross-multiplication,
a x c = b x x and x = a x c / b
Example 1:-15 men do a task in 28 days. In how many days will 21 men do it?
Obviously more men will do the work in less time and we have the proportion:-
21 / 15 = 28 / x and x = 28 x 15 / 21 = 20 days
Example 2.- If a task takes 40 days for 12 men, how many men will be required to do it in 24 days?
Obviously more men will be required to do the task in less time, in the ratio 40 to 24
40 / 24 = x / 12 and x = 40 x 12 / 24 = 20 men.
Natural, or Log. Sine; Cosine; Tangent, etc.- Use Datum line to read across from given angle on scales Nos. 5, 6, 7, to scale No.1 for natural values of sine, tangent etc., or to scale No. 3 for log. Values. Note the following:-
Cos = sin of complement.
Cot = tan of complement
Cos 60° = sin(90-60)° = sin 30°
Cot 60° = tan(90-60)° = tan 30°
All sines of angles on scale No.5 lie between 0.1 and 1.0 in value on scale 1.
All sines and angles on scale No. 7 (which are found on scale 1 in a similar manner) lie between 0.01 and 0.1 in value on scale 1.
Triangles; Useful Notes.-If A, B, C is a triangle, the angles of which
are A, B, C, and the sides opposite these angles are respectively a, b, c,
Then A + B + C = 180
a/b= sinA/sinB b/c = sinB/sinC c/a = sinC/sinA
a2 = b2 + c2 - 2 bc cosA
N.B.-Cos A is itself minus, and the whole of the last factor becomes plus if A is
greater than 90°.
If A is 90° the last factor disappears.
Sin(180-A)=sin A
Cos (180 - A)= - cos A
Cotan A = tan (90 - A)
Area of triangle = a b sin C/2
Tan (A-B)/2 = (a-b)/(a+b)
Cotan(C/2); Cotan (C/2) = tan (A+B)/2
The last two formulae are much used for solving triangles when two sides and the included angle are known.
If in a triangle A, B, C, the angle C is a right angle (90°), and the sides opposite the angles are respectively a, b, c letters arranged clockwise
Sin A = a/c; sin B = b/c;
cos A = b/c; cos B = a/c
Tan A= a/b; Cotan A
= b/c; secant A = b/c
Cosecant A = c/a
If C is not a right angle, the sine cosine, etc., still have the same values, but a and b are not now the sides of the actual triangle, but of an imaginary triangle with B C perpendicular to A.
The circle is divided in 360 degrees. Each degree is divided into 60 ' (minutes); each minute is divided into 60" (seconds), but seconds are rarely considered.
For angles below about 6°, tangents can be read off on the sine scale for small angles (scale 5).
The tangent is very slightly greater than the sine, but at 2° the error is only about one-sixteenth of one percent, which is too small to be read on the calculator or any ordinary slide rule.
If the sine or tangent of an angle is less than 0.01, use sine scale 7, but divide the angle by 10. Thus the angle whose tan is 0.00407 is one tenth of 2° 20'; that is 14 minutes. This is specially used in solving triangles with either two angles almost equal or with one very small angle.
FOWLER'S (CALCULATORS) LIMITED
Tel SALe 1433. Established 1898 Telegrams "Scientific, Manchester"
HAMPSON STREET WORKS, SALE, MANCHESTER
| Return to | Fowler in non-standard rules in collection |
| Fowler in trade in collection |