| Slide rules HOME page | INSTRUCTIONS | CONTENTS |
SECTION TEN
THE ELECTRICAL RULE
Dynamo and Motor Efficiencies - Volt Drop - Duplicate C & D Scales - Reciprocal Scale - Time Saving.
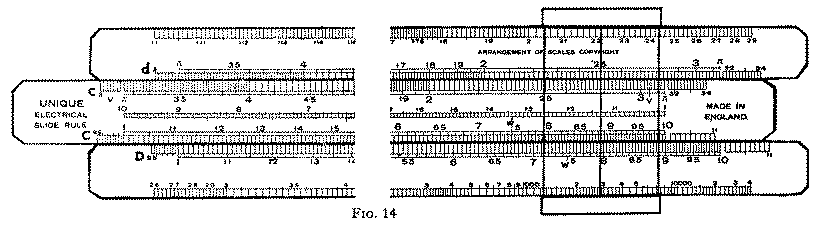
THE rule illustrated in Fig. 14, is designed for general purposes, but has some special features particularly related to electrical calculations.
The two scales of temperature, Fahrenheit on the upper part of the stock, and centigrade on the lower part, give a ready means of converting from either thermometric scale to the other by projection, and in addition they are designed so that the variation in resistance of copper conductors due to change of temperature may be determined quickly. (These two scales lie in the part of the rule cut out in Fig. 14.)

Example: A copper wire has a resistance of 2.8 ohms at 20°C. Find its resistance at
5° C. and 200° F.
Set X to 20° Cent. 28C to X. X to 5° Cent.
Read 2.63 ohms under X in C.
Set X to 200° Fahr.
Read 3.6 ohms under X in C.
In some makes of slide rules special 5" scales are fitted for calculating efficiencies of dynamos and motors. In the rule illustrated the same end is achieved with the aid of gauge points, and the efficiencies are found in 10" scales. These efficiencies are always of the order of 80% and 90%, and, therefore, they are found in the crowded parts of the scales. The advantage of using a 10" scale in place of the 5" scale employed in other rules, is obvious.
Example: Calculate the efficiency of a dynamo which gives an output of 33.4 kw. for
51.6 h.p.
To 334D set 516C.
Read the efficiency, 86.6% in d opposite the gauge point N in c.
Problem 43. Calculate the efficiency of a motor which develops 161 h.p. for 137 kw.
(To h.p. in D set kw in C. Read efficiency in D or d opposite gauge
point W in C or c.)
In the case of direct current or induction free alternating current, the drop in potential along a copper conductor is obtained easily. Volt drop is given by the formula (I x l) / (c x a) in which I is current in amperes, l is length of conductor in yards, c is conductivity of copper, and a is section of conductor in circular mils. (Circular mils = diameter of wire in thousandths of an inch squared.) The point V shown near each end of the c scale is used; it is the reciprocal of the conductivity of copper at 60° F. If the temperature differs much from 60° F., a correction should be made using the Fahr. scale as explained above.
Example: Calculate the volt drop in a copper conductor 208 yards long, .18"
diameter, carrying a current of 20.4 amps.
1802 = 32400.
Set 1C to 204D. X to 208C. 324C to X.
Read 39.9 in d above V in c.
Volt drop: 39.9.
The illustration shows that the A and B scales, which we have pointed out earlier are of little value, have been omitted, and in their place 10" scales identical in dividing and numbering with the C and D scales are substituted. These two scales are designated by c and d, and they are so positioned on the rule that p in d is immediately over 1 and 10 in D. This principle of displacing one scale relative to a similar one has been explained in Section 8. In the rule now under review all values in D are multiplied by p, by the simple process of projecting by means of the cursor from D to d, and conversely, values in d are divided by p when projected across to D.
There is a great number of practical problems in which p appears. Calculations relating to areas of circles, volumes and surfaces of spheres and cylinders, etc., necessitate the inclusion of p, and this arrangement of scales facilitates the manipulative operations of the rule. p = 3.14.
Example: Calculate the area of millboard required to make a cylindrical tube 2¼"
diameter, 14" long.
Set 1C to 14D. X to 2.25C.
Read in c under X.
Result: 99 square inches.
We have seen that when using the C and D scales of a standard slide rule the result sometimes is off the scale and it becomes necessary to re-set the slide by traversing it through its own length. This need never happen with the duplicated scales, since if the result is off D scale, it will be found on the d scale.
Another valuable characteristic of this rule is the additional facility it gives for setting quickly the slide and cursor, which need never be moved more than half the length of the rule for any operation.
If we remember that multiplication is effected by using the scales to add together the logarithms of the factors, the manipulation of the rule will quickly be appreciated. We are confident that many people who for years have used a slide rule equipped with the A, B, C and D scales would discard it for one giving greater facilities, if they would investigate the possibilities of other types. We will, therefore, carry our discussion of the duplicated C and D scales further and give a typical example of combined multiplication and division.
We will first take the simple case of 4 x 3. If we elect to perform this multiplication by using C and D only, we set l0C to 4D and read 12 in D under 3C. With the same setting of the slide, we also find the answer 12 in d above 3 in c, and very close to the 4 we commenced with. Now if we used the cursor in setting l0C to 4D, and we had other factors in our multiplication, we should need only to move the cursor about a quarter of an inch to pick up the 3 in c, whereas we must move it several inches if we work on the C and D scales only.
This simple exercise illustrates the saving in movement of slide and cursor when the two portions of the scales are used. We can go a step further and show how even shorter movements of the slide and cursor are possible, but this involves a complication which we prefer to avoid at this juncture. We refer to it again at a later stage.
If the reader will work through, step by step, the example following this paragraph, he will find no difficulty in using these duplicated scales, and provided he has had some previous experience of slide rules, we predict that he will prefer this type of rule to the more usual form.
Example: Evaluate (4 x 8 x 6 x 9) / (3 x 2 x 16).
To 4D set 3C.
Set X to 8c. 2c to X. X to 6C. 16c to X. X to 9c.
Result: 18 in D under X.
It is unimportant whether the first factor is selected in D or d, but we prefer to work as much as possible near the middle part of the rule; we choose our scales accordingly and adopt the following methods:
First method. - Having selected the first factor in D or d, and marked its
position with the cursor, we move the slide to bring the second factor under X. The second
factor lies in C and c, and we take the one nearest to the cursor. We next move the cursor
to the third factor in the same C or c scale in which the second factor was selected. If
we proceed in this manner of always taking the factors in pairs and in the same C or c
scale, the result will lie in the scale in which we selected the first
factor.
Second method. - There is an alternative procedure which may be adopted. We may start with the first factor in D or d, and bring into coincidence with it the second factor in the adjacent C or c scale. We then move the cursor to the third factor in C or c, selecting that which necessitates the least movement of cursor. The intermediate result will lie in the D or d scale which is adjacent to C or c scale in which the third factor was selected.
These instructions sound difficult, and in fact it is not easy to express them in words, but there is nothing complex to learn. The best way is to work through a few easy examples, and we think the reader will then agree that the duplicated C and D scales allow for more rapid working, and lead to greater accuracy.
The two methods of working we have defined may be used in conjunction with one another. We have adopted this procedure in the worked example above; the reader will see that we used the second method when using the factors 3 and 8, the second method for factors 2 and 6, and the first method for factors 16 and 9.
The reader will soon discover what appears to be a difficulty. Let us revert to the multiplication of 4 x 3. Set X to 4D. 1c to X. Result is 12 in D under 3c. Close to the 4 in D lies 3 in C, but if we project 3C across the slide to d we notice the answer is apparently in error, the cursor line falling a little below 12d. We also find in a similar manner the 2C falls below 8d, and 5C below 20d. In fact, all the values in C when projected into d give readings slightly below 4 times the values in the C scale.These discrepancies are not errors in the rule, but arise as a result of the manner in which the scales are placed relative to one another.
If the cursor has two hair lines drawn on it, at a distance of .058" apart, the
apparent departures we have observed may be allowed for. Returning to our simple 4 x 3
example, we first set the cursor X to 4D then brought the 1c to X. If now we place the
left-hand cursor line over 3C, the right-hand line will give the correct result 12, in d.
We must, therefore, bear in mind, in any operation in which we cross the slide to select
our second factor and re-cross to select the third factor, we must
cross the slide again, using the double line when reading the result. We do not recommend
the use of the double-line cursor, as it is liable to lead to errors, especially when we
are involved in a series of operations. If the multiple-line cursor is used, it is
advisable to use one which has a staggered line quite separate from the central index
line. The latter can be used in the normal way, and the former for the special purpose.
At the end of this section we make a brief mention of the type of slide rule with duplicated C and D scales which does not require a double-line cursor for the operations we have just discussed.
This scale lies along the middle of the slide and inspection of it discloses that it is divided in the same way as the C and D scales, but it is reversed and reads backwards, from right to left. We will designate this scale by R, as in the commercial rule.
By projecting direct from C to R, or vice versa, we obtain reciprocals. The reciprocal of any number being the result obtained by dividing 1 by the number, e.g. the reciprocal of 5 is one-fifth or .2.
Square roots are conveniently obtained with the aid of this scale. We set the 1 or 10 of C to the number whose square root is required in D, and then slide the cursor along until we find a position in which the readings under the cursor index in scales R and D are identical. These readings are the square root of the number.
If the original number lies between 1 and 10, we shall set 1C to it; if between 10 and 100, we use the l0C index. For any number outside the 1 - 100 range we shift the decimal point in steps of two places to bring the number between 1 and 100, and after finding the square root, move the decimal point in the opposite direction one place for each step of two places originally made. This procedure is more fully described in Section 5.
There is another way of determining which index of Scale C should be used, or when scales A and D are being employed which half of scale A should be selected: The rule is: If the original number has an odd number of digits preceding its decimal point, or, when less than unity, has an odd number of ciphers immediately following its decimal point, the left-hand half of scale A must be used, or, if the reciprocal scale is being employed, l0C should be set to the number in D. When the number of digits preceding, or the ciphers immediately following the decimal point in the original number is even, the right-hand half of scale A or the 1 of C must be used.
We mention this method of extracting square roots only as a matter of interest. We do not recommend it in practice. It is always better to use A and D scales, or if these are not available, the log-log scale or the method explained in Section 4 using C and D.
In conjunction, the C, D and R scales give a means of multiplying together three factors at one setting of the slide. Some of the standard rules, i.e. those supplied with A, B, C and D scales, are equipped with a reciprocal scale, and the property of multiplying three factors at one setting is usually claimed for this type of rule. We will investigate this feature.
Multiplication of three factors is effected by: setting the cursor to one factor in D; moving the slide to bring the second factor in R to X; reading the result in D (or d) opposite the third factor in C (or c).
Take the simple example of 4 x 5 x 6, the result of which, as we can see without using the rule, is 120.
Set X to 4D. SR to X. The result, under 6C in this example, is off the D scale, but if we are using a rule with duplicate C and D scales, we find the answer, 120, in d opposite 6c. If, in addition to the R scale, we have only the C and D scales available, it is necessary to traverse the slide after the first setting in order to obtain a reading, and there is no advantage in adopting this method. In a rule equipped with duplicate C and D scales, the result will always be obtainable at one setting of the slide, but occasionally it will be necessary to select the first factor in the d scale, and when this procedure is followed, the third factor must be projected across the slide to obtain the final reading on the opposite side of the stock (in d).
Dividing by two factors with a single setting of the slide, e.g. 4.26 / (.035 x 2.88) can be effected with scales C, D and R. The cursor is used to mark the numerator in D (or d), one factor of the denominator in C (or c) is placed under X by adjusting the slide, and the result is read in D (or d) opposite the remaining factor in R. In this type of calculation, when using the ordinary rule, we find the same limitations, the result fairly frequently being off the scale. When this occurs, a second setting becomes necessary, and again there is no saving in time over and above using the C and D scales in the usual manner. The rule with duplicated C and D scales is much more convenient, the result always being obtainable at one setting of the slide. The method we invented in connection with the precision rule, in Section 9, for determining in which scale, D or d, the result lies, applies in exactly the same manner to our present problem; we ask the reader to turn back and study this method again; it is very simple.
In applying the method, regard scale R as being part of scale C, and if the two factors used lie in R and C, imagine them as being in one scale. This is easy to remember for, although the scales are in reality quite separate, they are intimately connected by virtue of their reciprocal relationship.
Example: We will now work an example with a number of factors to illustrate the time-saving effected, by employing scales C, D and R, and using the type of rule in which 1c lies immediately over l0C, as this will not necessitate the use of the staggered-line cursor.
Evaluate 3.42 x .722 x 5.08 x 13.5 x 2.12 x .38 x .0818.
| Set X to 342D | B | The
symbols for check on final scale reading are: B BT BT BT, or in the more condensed form -
Bx/ indicating that the result must be read in the top scale, i.e. in d, and we read the answer there as 112. Approximation gives a result about 10. Our answer, therefore is 11 .2. |
| 722R to X | B | |
| X to 508c | T | |
| 135R to X | B | |
| X to 212c | T | |
| 38R to X | B | |
| X to 818c | T |
The reader will see that there is a considerable saving in the movements of slide and cursor as compared with those necessary if multiplication is effected by C and D scales alone, and if we frequently have to make computations of this type, the method we have just used is worth adopting.
There is no saving in using the R scale in combined multiplication and division, since in such cases we can use the method of dividing by one factor and multiplying by another at one setting of the slide, as fully explained in Section 4.
Time saving can be effected when there are several factors in the divisor, and we will leave the following example for the reader to solve:
Problem 44. Evaluate 166 / (2.1 x 3.2 x .85 x .196 x 4.2 x 34.2)
We would sum up a rather controversial subject in this way. If our work only occasionally involves these calculations, we would use the C and D scales in the normal way and not resort to the use of the R scale, since we may make errors by occasionally changing our way of working. But our work may involve a long list of three-factor calculations, all alike in form, only differing in the actual numbers used. We think it may now be an advantage to use the C, D and R scales. Even with the standard type of rule, some results will appear at one setting of the slide, and this will effect a saving of time. With the C and D scales in duplicate the result will be always obtained at one slide setting, resulting in still further time saving.
We prefer to let the reader make his own decision in cases similar to the preceding example and problem. Time saving is effected by using the C, D and R scales in conjunction; it is a question of whether, when an isolated computation involving several factors in either numerator or denominator arises, it is worth while changing our method of working.
Expressing an opinion, with which some slide rule users will disagree, we would say there is very little advantage to be derived from the reciprocal scale when used in conjunction with the normal C and D scales.
If the C and D are duplicated, the reciprocal scale is perhaps worth its place.
© Hodder Stoughton, reproduced with permission.