| Slide rules HOME page | INSTRUCTIONS | CONTENTS |
SECTION SEVEN
THE TRIGONOMETRICAL SCALES
Sine and Tangent Scales - Solution of Triangles - Navigational Problems - Navigational Units and Formulae - Wind and Drift Problems - Interception Problems - Calculation of True Track and Distance.
THE scale equipment of what may be termed the standard 10" slide rule Comprises scales A, B, C and D on the faces of the slide and the stock, together with three scales on the back of the slide. These three scales are (i) a logarithmic scale of sines of angles usually denoted by S; (ii) a logarithmic scale of tangents of angles usually denoted by T; (iii) a scale equal in length to the D scale divided into 10 equal parts and each of these parts subdivided into fiftieths; this scale is generally designated by L and is designed for reading common logarithms.
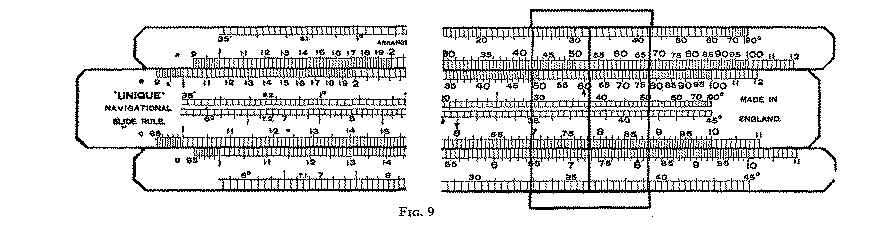
In those models of the "Unique" range of slide rules which are equipped with trigonometrical scales the S and T scales will be found on the faces of the rule, or as in the Brighton rule on the edge of the stock. This layout of scales facilitates manufacture, reduces the cost of production and contributes to the possibility of supplying slide rules at what are often regarded as absurdly low prices. In some models the S and T scales are carried by the stock, in others by the slide, and it will be found that some calculations are made more easily with one arrangement and others more easily with the alternative.The logical step is to equip both stock and slide with S and T scales; this has been done in the Navigational rule which is illustrated, reduced in size, in Fig. 9. For trigonometrical work we believe this rule is superior to any other obtainable, and in examples which follow we shall be using it.
If you possess a slide rule in which the S and T scales are on the under-surface of the slide, you will find no great difficulty in making the necessary modification to these instructions. You will find the slide can be withdrawn and turned over so that what is generally the under-surface is brought uppermost. In this inverted position some problems can be quickly solved; others may be dealt with when the slide is fitted in its normal position, and you will find fixed index marks in the slots at the ends of the rule which are used in conjunction with the trigonometrical scales.

In Fig. 9 the reader will recognise the A, B, C and D scales. In addition there are two identical sin scales designated by S1 and S2, and two tangent scales denoted by T2 and T1. The reader should first carefully examine the manner in which the S and T scales are graduated, since these do not altogether follow the principle of decimal subdividing. The wider spaces of the S scale and the whole of the T scale are subdivided in terms of minutes. The smaller spaces towards the right-hand end of the S scales represent unit degrees.
To find the sin of any angle we project with the aid of the cursor direct from S1 to A.
Example: Find the sines of 2° and 40°.
Using X, we find in A under 2 and 40 of S1 the values 348 and 643. The
actual sines are .0348 and .643
We assume that all readers remember that sin 30° is .5. Sin 40 must be, therefore, somewhat greater than .5. If when projected from S1 we find the result within the 1 to 10 part of scale A, it must be prefixed by the decimal point and one cypher. If the result falls within 10 to 100 part of the scale, the decimal point only should be inserted before the actual figures. For finding sines of angles less than 35', other means must be adopted, and for sines of angles approaching 90° the slide rule is unreliable. We recommend the use of a table of sines in preference to the indirect methods which can be employed.
To find the tangent of any angle, project from T1 to D. We bear in mind that tan 45° is 1, and we, therefore, insert the decimal point immediately before the reading obtained in D.
Example: Find tan 20°.
Set X to 20T1, and read in D 364; result: .364.
Tangent of angles between 45° and 90° should be obtained by finding the reciprocals of the tangents of the complementary angles.
Example: Find the tan of 55°.
Complementary angle is 35°. Set X to 35T1 and in D read
.7. The reciprocal of .7 is 1.43, which is the tan of 55°.
(NOTE. - If your slide rule is provided with a reciprocal scale you may read the 1.43 direct without having to divide 1 by .7.)
The sines and tangents of small angles differ so little from one another that tangents of angles less than 6° may be taken as sines without appreciable error. For example, sin 4° = .0698, and tan 4° = .0699; the difference between these two values is too small to be observed in slide rule calculations.
Cosines of angles are obtained by finding the sines of complementary angles.
Example: Cos 54° = sin 36° = .588.
Cosecants, secants and cotangents should be obtained when required as reciprocals of the corresponding sines, cosines and tangents respectively. The following exercises illustrate the uses of the slide rule for the solutions of triangles. (To avoid conflict with the letters A, B and C used to denote the scales, we shall use K, L and M to represent angles, and k, l and m to represent the opposite sides of the triangle; also 2s to represent the perimeter, namely k + l + m.
Example: Given M = 25°, K = 90° and k = 5". Find the remaining angles
and sides of the triangle.
L = 90° - 25° = 65°.
l = 5 sin65°. m = 5 sin25°.
Set 100B to 5A.
X to 65S2. Read in A under X 4.53 the value of l.
X to 25S2. Read in A under X 2.11 the value of m.
Example: Given K= 90°, m = 4.2 and 1= 5.6. Find k, L and M.
tan M = 4.2 / 5.6. Set 5.6C to 4.2D, X to 10C.
M = 37° in T1, under X.
k= 4.2 / sin 37. Set X to 4.2A, 37S2 to X.
Read k = 7 in A above 100B.
Set 7B to 5.6A; X to 100B.
Read L = 53° in S1 under X.
(Check 37° + 53° = 90°.)
Problem 24. Given K = 90°, l = 5.5 and k = 12.9. Find L,M and m.
Problem 25. Given M = 21°, K = 90° and m = 1.8 Find k, L and l.
The examples and problems cited above refer to right-angled triangles. We continue with a few typical problems relating to triangles which are not right angled.
Example: Given l = 4.4, m = 5.2 and K = 64°. Find the remaining side
and angles.
k2 = 12 + m2
- 21m cos 64°
= 19.4 + 27.1 - 20.1 = 26.4.
Set X to 26.4A. Read 5.13 in D under X = k.
(l and m are squared using
scales A and D.)
To find the third term which is 2 x 4.4 x 5.2 x sin 26°.
Set X to 26S1, 100B to X, X to 88B, 100B to X.
Read 20.1 in A over 52B.
(There is no point in using the slide rule for operations which can easily be done mentally, e.g. 2 x 44 = 88, but only simple factors should be combined in this way as it is easy to make slips when using the slide rule and making mental calculations simultaneously.)
Now use the sine rule: sin L / l = sin M / m = sin K
/ k
Set X to 64S1, 513B to X.
Read in S1 over 44B, L = 50°; and over 52B,
M = 66°.
(Check 64° + 50° + 66° = 180°.)
Results: k = 5.13; L = 50°; M= 66°.
There are alternative methods of solving this problem; we might have used cos M = (k2 + l2 - m2) / 2kl, then L would have been found by 180° - K - M, or the cosine rule used again to find L. We would point out that if both L and M are found by sine or cosine rules, we get a very good check by seeing if the sum of the three angles is 180°. If the third angle is found by subtracting the sum of the other two from 180°, any error previously made is not disclosed. When using the sine rule the reader is reminded that the sines of supplementary angles are equal in both sign and magnitude, and it is necessary to determine which to take. A diagram drawn roughly to scale is the best means of selecting the appropriate angle.
Problem 26. Given k = 5.3, l = 7.1 and m = 3.1. Find K, L
and M.
(Use the cosine rule to find L, then the sine rule to find K and M.
Check against 180°.)
Example: Given K= 80°, L = 43° and m = 4.5. Find k, l and M.
M= 180 - 80 - 43 = 57°.
Set X to 45A; 57S2 to X;
X to 43S2 read l = 3.65 under X.
X to 80S2 read k = 5.3 under X.
Problem 27. Given K = 30°, L = 118° and l = 10.5. Find k, M and m.
Example: Given k = 53, l = 35 and L = 28°. Find K, M and m.
This is an example of the well-known ambiguous case with which the reader may be
acquainted. If he is not, we advise him to construct a diagram with the data given, and he
will find that the side 1 can be drawn in alternative positions giving rise to
two triangles. We must remember that side l is opposite angle L.
sin K = k sin L / l.
Set X to 28S1, 35B to X, X to 53B.
Under X read 45 in S1.
K is therefore 45° or 135°.
M is 107° or 17°, i.e. 180 - 28 - 45 or 180 - 28 - 135.
m = l sin M / sin L.
Set X to 35A. 28S2 to X.
X to 73S2 (= 180 - 107) and read in A 7.1
under X.
X to 17S2 and read in A 21.8 under X.
Results: K= 45° or 135°; M= 107° or 17°; m = 7.1 or 2.18.
Problem 28. Given k = 8, l = 10 and m = 14. Find the angles
and area of the triangle using the formulæ:
sin (K/2) = Ö ((s - l)(s
- m)) / lm
cos (L/2) = Ö (s(s
- 1)) / km)
tan (M/2) = Ö(((s - l)(s - k))
/ ( s(s - m)))
Area of D = Ö(s(s
- k)(s - l)(s - m)).
The reader will understand that it is not the function of this book to teach the principles of any branch of science or to establish formulae. The book embraces examples dealing with energy, friction, heat, deflection of Beams, strength of shafts, electricity, building, etc., and in no case do we deal with the underlying principles of any of these subjects. We are attempting to show how the slide rule can be employed quickly and easily to cope with the numerous computations which arise. For the principles and formulæ involved, the reader must consult the textbooks which are available if he needs such assistance. He will find several such textbooks in the Teach Yourself series.
One of the really fascinating characteristics of the slide rule is the ease with which it deals with some of the problems in trigonometry which are encountered during the navigation of a coasting or sea-going ship, or of an aircraft.
There are many proportional problems which arise in connection with aircraft or ships which have no bearing on navigation. For example, the time taken to cover a given distance for a known speed of craft, fuel consumption, conversion from one set of units to another, stowage and loading calculations. Problems of draught and trim and stability.
These problems require no use of trigonometry but can be solved with the aid of the C and D scales or with the use of the other scales we have already examined. We shall not include any examples of these types of problems, but proceed to examine some of those which demand trigonometrical treatment.
We shall, for the remainder of this section, use the Navigational rule which, in the 10" size, gives a satisfactory degree of accuracy for most problems. We would, however, mention that, if used, the 10/20 Precision rule or the Precision scales of the 10" Dualistic rule will invariably give a higher degree of accuracy. The disadvantages of using these rules lies in the fact that the values of sines and tangents must be taken from tables, since the trigonometrical scales are not included in the scale equipment of these two rules.
It will be noticed that more space is devoted to navigational problems in Section 7 than to any other single subject. This is because the Navigational rule which is the subject of this section, was designed to deal with the trigonometrical work involved in navigation and we felt that some additional exercises should be given. This rule was introduced in the early days of World War II for the benefit of air navigators, and it will be seen that the data given on the back of the rule, and the scales on the edges, are more concerned with air navigation than with ship navigation, but the problems met with in the two branches of navigation are generally similar and sometimes identical and the Navigational slide rule can be just as easily used for problems arising in ship navigation. The notes on air navigation were contributed by an experienced air navigator.
The slide rule may often be used instead of the traverse table.
Example: An 8½' pole standing vertically on a horizontal plane casts a shadow 18'
3" long. Calculate the altitude of the sun at the time of observation.
Over 85D set 1825C.
Move X to 1C.
Under X read 25T1.
Answer: altitude is 25°.
Example: A ship steering 10° S. of E. observes a light bearing 40° N. of E. After
steaming 8 miles the light bears 15° E. of N. Calculate the distances to the light at the
two observations.
1st angle from the bow = 50°.
2nd ,, ,, ,, ,,
= 85°.
Over 45S2 set 8A.
Over 50S2 read 867A.
Over 85S2 read 113A.
Distances 11.3 miles and 8.67 miles.
[Note: The above, is a correction of the version which appears in the book. The author had subtracted 50 and 85 from 180 and got 35!]
Problem 29. A ship sailing due N. sights two gas buoys bearing 020° and 035°. After sailing 8 miles the two marks were in line dead abeam. Calculate the distance between the two buoys.
Example: From a vessel steaming on a straight course a lighthouse was observed 38°
forward from the beam. The light was observed to be exactly abeam after the ship had
steamed a further 8.3 miles. Calculate the distance at which the light was passed abeam.
Over 8.3D set 38T2.Under 1C read 106D.
Answer:10.6 miles.
Note that this answer is obtained by dividing the distance run by the tangent of angle
forward from the beam. If this angle is above 45°, the result is obtained by multiplying
the distance run by the tangent of the complementary angle.
Problem 30. Find the answer to the foregoing example if the angle forward of the beam had been (a) 58°; (b) 45°.
The Haversine Formula is sometimes useful in dealing with problems which involve the solution of triangles, given the three sides.
Note.
Versine A = 1 - cos A
Haversine A = Hay. A = (1 - cos A) / 2.
Employing the usual symbols for plane triangles, viz. A, B, C, a, b, c, 2 s
= a + b + c,
Hav. A = (s - b)(s - c)
/ bc
Hav. B = (s - a)(s - c) / ac
Hav. C = (s - a)(s - b)
/ ab
Problem 31. If a = 7, b = 5, c = 4, find A, B and C.
Navigational Units and Formulae
Length of nautical mile at Equator, 6046 ft.
,, ,, ,,
,, ,,
Poles,6108ft.
Standard nautical mile (used in practice), 6080 ft.
1 knot = 1 nautical mile per hour.
1 cable = 600 feet.
dep. = D. long. x cos mid. lat.
= D. lat. x tan course.
= dist. x sin course.
D. lat. = dist. x cos course.
= dep. x cot course.
dist. = dep. x cosec course.
= D lat. x sec course.
tan course = dep. / D.lat.
D. long. = dep. x sec mid. lat.
Example: A ship steering a course 5. 28° E. is making a speed of 14 knots. Calculate
the D. lat. and dep. over a 3-hour run.
D.lat. = dist. x cos course.
Set 42A over 90S2
Over 28S2 read 197A
Over 62S2 (compl. course) read 370A.
Answer: D. lat. 37'; departure 19.7' E.
Problem 32. Given lat. 24° N. and departure 32 miles, find D long.
Example: A ship steamed on a course of 055° for 4 hours at a speed of 18 knots.
Calculate the departure and D. lat.
Distance is 72 miles.
Course angle is 55°.
use dep. = dist. x sin course
D. lat. = dist. x cos course
Set 90S2 under 72A.
Over 55S2 read 59A.
Over 35S2 read 41.2A.
Answer: Departure 59 miles E.; D. lat. 41.2' N.
Problem 33. A ship steamed on a course of 300° for a distance of 400 miles. Calculate D. lat. and departure.
Example: Calculate the distance from a light known to be 110' above sea-level at the
time when the light first appears above the horizon. Height of observer's eye 50'.
Use the formula below for distance of sea horizon; 1.15 ÖH.
Set 1B under 50A.
Under 115C read 8125D.
Set 1B under l10A.
Under 115C read 1207D.
Distance 8.125 + 12.07 = 20.195 miles.
Problem 34. The Spurn Light is 120 ft. high. At what distances will it be just visible
to an observer on the bridge of a ship, at height of eye of (i) 20 ft.; (ii) 40 ft.; (iii)
60 ft.?
To find the course to steer and ground speed along given track. Using scales S2 and A. Under the airspeed set the angle on the bow or quarter of the track that the wind is blowing. Under the wind speed read the drift angle. The drift angle, added or subtracted to the track, will give the course to steer. To find the ground speed: if the wind is a head wind, subtract the drift angle from the wind angle on the bow; if a tail wind, add the drift angle to the wind angle on the quarter. Above the resulting angle read the ground speed.
Example: Airspeed 126 m.p.h. Track 040° T. Wind velocity 20 m.p.h. from 090° T. (50°
on the bow).
To 126A set 50S2.
Under 20A read 7S2.
Over 43S2 (50° - 7°) read 112A.
Result: Course to steer 043° T.; ground speed 112 m.p.h.
Example: Airspeed 97 knots. Track 352° T. Wind velocity 15 knots from 110° T (62° on
the starbd.quarter).
To 97A set 62S2.
Under 15A read 8S2 (drift).
Over 70S2 (62° + 8°) read 103S2.
Result: Course to steer 360° T.; ground speed 103 knots.
Note that when the drift is less than 1 degree, the ground speed should be found by adding
or subtracting the wind speed and the airspeed.
To find the wind velocity, knowing the track and ground speed, course and airspeed.
On scale A mark the airspeed and ground speed with the cursor and a light pencil
mark. Adjust the slide until the number of degrees read between the airspeed and the
ground speed markings equals the drift angle, i.e. the difference between the course and
the track. Above the drift angle on scale S2 read the wind speed on scale
A. Under the airspeed read the wind direction as an angle on the bow or quarter of the
track, or under the ground speed as an angle on the bow or quarter of the course. Note
that if the G/S is less than the A/S, the angle is on the bow, and if the A/S is less than
the G/S, an angle on the quarter.
Example: Course 137° T. Airspeed 150 m.p.h. Track 142° T. Ground speed 130 m.p.h.
Mark the scale A at 130 and 150. Adjust the slide until a difference of
reading of S degrees on scale S2 is obtained between the above markings. In
this example 29° and 34° will be found to correspond. On scale A above 5° read 23.4
m.p.h. (wind speed). The wind direction is 34° on the bow of the track, and is therefore
108° T. as the drift is to starboard.
To find the wind speed and ground speed, knowing the course and airspeed, drift angle and wind direction.
This method is particularly useful when a flight is being made over the sea and it is desired to know the ground speed. In such cases the drift angle can nearly always be found by a drift sight or back-bearings of an object dropped from the aircraft, but it is not such a simple matter to determine the ground speed. It is a known fact, in a steadily moving air mass, the difference between the wind direction at the surface and the wind direction at a reasonable height remains nearly constant with the changes of surface wind direction.
This difference can be ascertained at the departure point from meteorological information available and applied to the direction of the surface wind obtained during the flight by bearings of the wind lanes on the sea surface. It has also been found that in practice a reasonably accurate forecast of the direction of the upper winds can be given by a meteorologist, whereas difficulty is sometimes experienced in forecasting the speed. The wind direction can also be ascertained by noting the direction of movement of cloud shadows on the surface. With these various sources at the navigator's disposal little difficulty is usually encountered in finding the wind direction.
Example: Airspeed 110 knots. Course 136° T. Track 142° T. Drift 6° to starbd. Wind
direction 348° T.
The difference between the track and wind direction is 206°. The wind angle is therefore
26° on the quarter, a tail wind. Therefore 26° added to 6° (the drift) will give the
angle to use to find the ground speed.
To 110A set 26S2.
Over 6S2 read 26.2 (wind speed).
Over 32S2 read 133 (ground speed).
Result: Wind speed 26.2 knots; ground speed 133 knots.
To find the new track and wind speed after an alteration of course.
This method is not mathematically correct, but is sufficiently accurate when it is desired to know the track and ground speed immediately after an alteration of course. In practice, drift should be checked by observation as soon as possible after any alteration of course, so it should never be really necessary to calculate the D.R. track.
Example: Before alteration of course the track was 045° T. Wind velocity 20 m.p.h.
from 095° T. True airspeed 140 m.p.h. Drift 6¼°. Course steered 051° T. Course is
altered to 120°. The wind is now 25° on the port bow of the aircraft, previously it was
44° on the starbd. bow.
To 6.25A set 44S2.
Over 2SS2 read 3.8A.
Result: The new drift is 3° 48', and the new track is 124° to the nearest degree.
To find the new ground speed:
To 20A set 3° 48' S2 (wind speed).
Move X to 140A.
If the angle under the cursor is not an even degree or half degree, adjust the slide accordingly, to bring the nearest half or whole degree under the cursor. Then move the cursor 3° 48' to the left (as the wind is ahead) and read on scale A the new ground speed, 122½ m.p.h.
If course is being altered frequently, as it would be if a search of some kind were
being carried out, it would be far easier and decidedly more accurate to keep a plot of
air courses on the chart. When it is desired to know the D.R. position, the total windage
affecting the aircraft during the search can be applied to the air position. This can most
effectively be accomplished by plotting a wind scale, subdivided into intervals of, say
five minutes. The distance that the aircraft has been
blown downwind can then be conveniently stepped off with dividers from the air position.
Thus if the air courses flown have totalled 55 minutes from the last fix, then 55 minutes of wind is used. The wind scale is, of course, constructed to the same scale as the distance scale of the chart or map.
It should always be borne in mind that the errors of D.R. navigation are accumulative; therefore the more observations of drift, ground speed or position that can be made, the more accurate will be the final result.
It will be seen in all these problems that the drift angle is always subtracted from the wind angle to the track for head winds, and added for tail winds. Little difficulty will be found in remembering this, for it will always be readily seen when using the slide rule, for a head wind will always reduce the ground speed, and a tail wind will increase it.
In theory, the most accurate method of determining the course to steer to intercept a moving surface-vessel is by plotting, and for examination purposes this is the safest method to adopt. In practice, however, this very seldom works out, because changes of wind or weather en route often necessitate an alteration of course, and consequently the time and labour spent in solving the original problem is wasted. Again, the problem often arises: When the ground speed during the flight is not what it was estimated to be, how much has course to be altered? Theoretically, a new interception problem should be worked out, but this is a rather lengthy procedure. The following method, using the slide rule, gives a simple solution to this type of problem.
Example: Bearing and distance of ship 012° 282'. Ship's course and speed 125° 17 knots. Airspeed 120 knots.Wind velocity 22 knots, from 247°.
Find the angular difference between the relative bearing and the ship's course, i.e.
125° - 12° = 113° or 67° on the "quarter" of the relative
bearing. Estimate the ground speed of the aircraft. This can be done quite roughly, as a
few knots either side of the correct ground speed is negligible. Ground speed is therefore
estimated to be 125 knots.
Under 125A (G/S) set 67S2.
Traverse slide.
Under 17A (ship's speed) read 7° 11' in S2.
This will give the angle the track out makes with the relative bearing. The track is
therefore 019° T.
Find now the angular difference between the wind direction and the track. 019° + 180°
= 199° - 247° = 48° on the quarter.
Under 120A set 48 S2.
Under 22A read 7° 50'S2.
Over 55° 50' S2 read 133½A.
As the wind is a tail wind, 7° 50' and 48° are added, and the true ground speed out is 133½ knots. If the first part of the problem is re-checked, using the correct G/S of 133½ knots, it will be seen that the angle between the relative bearing and the track is still approximately 7°.
The drift has been found to be 7° 50' starboard.
The course to steer is therefore 011°.
If, after the course has been set, an alteration in the estimated ground speed is discovered, the amount which course has to be altered (to maintain the relative bearing of approach) can be found by carrying out the procedure adopted in the first part of this example, using the new ground speed, and thus finding the new track to intercept. This track can then be maintained by drift observations and slight alterations to course. During the latter stages of the flight, if large changes of drift or ground speed are found, a new relative bearing should be measured between the calculated D.R. positions of the ship and the aircraft, at the same instant of time. If this is done for a few minutes ahead, and a change of relative bearing is discovered, the new course to steer can be determined by using the new angle between the new relative bearing and the ship's course.
The estimated time of interception should be calculated by measuring the distance along the track, and applying the measured ground speed. If the speed of closing is used along the line of relative bearing, some difficulty will been countered in the calculation of a new E.T.I. when it is found that the G/S is not what it was estimated to be.
The Calculation of True Track and Distance
The true track and distance by the middle latitude formula.
Formula:
dep. = D. long. x cos mid. lat.
tan tr. = dep. ¸ D. lat.
dist. = dep. x cosec tr.
D.lat. x sec tr.
To find the rhumb line track and distance from Calais to Heligoland.
| Calais | lat | 50° 58' N | long | 1° 51' E. |
| Heligoland | 54° 11' N. | 7° 53' E. | ||
| D.lat | 3° 13' N | D. long | 6° 02' E. | |
| 193' | 362' | |||
| mid. lat | 52° 34' 5 |
To find the departure.
Set 362B to 90S1.
Under 37° 25½S1 (comp. of mid. lat.).
Read 220B.
Departure 220'.
To find the true track.
Rule: Always set the larger value of D. lat. and dep. on scale C, and the smaller value on
scale D.
Over 193D set 220C.
Set X to 10C.
Under X read 41° 15' in T1.
As the dep. is greater than the D. lat. the track is obviously greater than 45°.
Therefore the complement of the angle 41° 15' is used. The track is always named the same
as the D. lat. and the D. long.
True track = N. 48° 45' E. or 049° T. to the nearest half degree.
To find the rhumb line distance.
Set X to 48° 45' S1 and move 220B to X.
Under 90S1 read 293B.
Rhumb line distance 293 nautical miles.
A check on the answer can be obtained by setting X to 41° 15' (complement track) and reading 293' (D. lat.) on scale B.
To find the rhumb line track and distance from Calais to Gibraltar.
| Calais | lat | 50° 58' N | long | 1° 51' E. |
| Gibraltar | 36° 04' N. | 5° 26' W. | ||
| D.lat | 14° 54' S | D. long | 7° 17' W | |
| 894' | 437' | |||
| mid. lat | 43° 31' |
To find the departure.
To 90S1 set 437B.
Under 46° 29'S1 read 317B.
Departure 317'.
To find the true track.
Over 317D set 894C.
Set X to 10C.
Under X read 19° 30' T1.
True track S. 19½° W. or 199½° true.
To find the rhumb line distance.
Set X to 19° 30' S1.
Set 317B to X.
Under 90S1 read 951B.
Rhumb line distance 951 nautical miles.
Distances of over 200 miles should always be calculated in preference to measuring the distance by dividers on the map or chart. Again, it is always easier and more accurate to calculate the track and distance between places which are not on the same map or chart sheet. A little practice with the slide rule will enable this problem to be solved more accurately, and in a shorter time than it would be if traverse tables were employed.
The great circle track and distance, etc.
In air navigation, the great circle track has other uses than the saving in distance during a long flight. It can be used to avoid ranges of high mountains or prohibited areas without increasing the distance flown, and in flights, when it is desired to bring the track of the aircraft within visibility distance of some landmark, to assist navigation, when by flying the rhumb line track the landmark would have been missed altogether. It is, of course, not always possible to utilise the great circle track in this manner, but these advantages should not be forgotten when planning a flight of even moderate distance.
To calculate the problems involved, by spherical trigonometry, is a very tedious procedure. When, in order to shorten the work, short tables are employed, an added disadvantage is encountered, namely the necessity of having to choose two points near the departure point and destination to obtain angles to fit the tables.
By using the slide rule all these difficulties are overcome, for the solution is both rapid and accurate, and the actual positions of the chosen places can be used.
To calculate the great circle distance.
Formula:
tan. lat. A x tan lat. B + cos D. long.
(If lat. A and B are in the same hemisphere.)
tan lat. A x tan lat. B - cos D. long.
(If lats. A and B are in different hemispheres.)
The result is called C.
C x cos lat. A x cos lat. B = cos distance.
N.B. - The rules regarding the plus and minus to D. long. are reversed if the D. long, exceeds 90°.
Example:
Position A, lat. 38° 45' N., long. 9° 30' W.
Position B, lat. 40° 25' N., long. 73° 15' W.
Difference of longitude is 63° 45' W.
Over 38° 45'T1 set 45T2.
Under 40° 25' T2 read 683D.
i.e.tan lat. A x tan lat. B = .683.
Under 26° 15'S1 (comp. 63° 45').
Read 442A i.e. cos D. long. = .442.
.683 + 442 = 1.125 (as A and B are in the same
hemisphere).
Under 51° 15'S1 set 90S2 (comp. lat. A).
Move X to 49° 35'S2 (comp. lat. B).
Set 1B to X.
Read 48° 03' S1 over 1.125B.
The angle 48° 03' is read as a complementary angle to that indicated on scale S1,
as the answer is the cosine of the distance.
Great circle distance 48° 03' or 2883 nautical miles.
In the latter process the formula is 1.125 x cos lat. A x cos lat. B =
cos distance.
Note that the scales S1 and S2 are sine scales, and to use these scales for cosines the complementary angles must be used. After becoming acquainted with the use of the trigonometrical scales, the beginner will be able to select the complements of angles quite easily from the sine scale by counting the degrees from the right-hand index, or from an easily recognised complement, e.g. 60°, 45° or 30°.
The initial track.
Formula:
sec. lat. A x sin lat. B x cosec distance = A (opposite name to lat. A).
tan lat. A x cot dist. = B (same name as lat. B).
The algebraic sum of A and B is the cosine of the initial track. Lat. A 38° 45' N.
Lat. B 40° 25' N. Distance 48° 03'.
To find A.
Under 51° 15' S1 (comp. 38° 45') set 40° 25' S2.
Move X to 48° 03' S2.
l00B to X.
Under 90S1 read 112B.
To find B.
Over 38° 45' T1 set 45T2.
Under 41° 57' T2 (comp. dist.) read 721D.
1.12 - .721 = .399 (see rules above)
(A is South, B is North).
.399 is the cosine of 66° 30'. This is read from the scales A and S1
by setting the cursor over the required figures.
Initial track N. 66½° W. or 293½° T.
To find the latitude of the vertex.
Formula:
sin init. tr. x cos lat. dep. = cos lat. vertex.
init. course 66° 30'. lat. dep. 38° 45' N.
Set 90S2 under 66° 30' S1.
Over 51° 15' S2 read 44° 20' S1 (as a
cosine).
Lat. of vertex 44° 20' N.
To find the longitude of the vertex.
Formula:
cosec lat. dep. x cot init. tr. = tan difference of longitude
between point of departure and longitude of vertex.
lat. of dep. 38° 45' N. Init. tr. 66° 30'.
Under 38° 45' S1 set 100B.
Under 1A read 16B.
Over 16D set 1C.
Under 23° 30' T2 (comp. 66° 30') read 34° 50' T1.
The longitude of the vertex will be 34° 50' W. of the point of departure, and will
therefore be in long. 44° 20' W.
To find the latitudes in which the great circle track will cut given meridians.
Formula:
tan lat. = tan lat. vertex x cos D. long, between the longitude of the
vertex and the given meridian.
Meridian 19° 30' W. Lat. vertex 44° 20' N. D. long, is 24°
50'.
From scales A and S1 find cos D. long. 24° 50' equals
.907.
Over 907D set 45T2.
Under 44° 20' T2 read 41° 33' T1.
Lat. of tr. in meridian 19° 30' W. = 41° 33' N.
To find the track in any latitude.
Formula:
sin tr. = sec lat. x cos lat. vertex. Chosen lat. 40°.
Lat. of vertex 44° 20' N.
Under 90S1 set 50S2 (comp. of 40°).
Over 45° 40' S2 (comp. 44° 20') read 69S1.
Tr. in lat. 40° N. is N. 69° W. or 291° T.
For calculation of a D.R. or air position.
Formula:
dep. = dist. x sin tr.
D. lat. = dist. x cos tr.
D.long. = dep. x sec mid. lat.
To find the D.R. position after a run of 3 hours along a track of 242° T. at a G/S of 138 knots, from a position lat. 50° 30' N., long. 9° 20' W.
242° T. is a bearing of 5.62° W. 3 hours at 138 knots represents a run of 414 nautical miles.
To find the departure.
Under 414A set 90S2.
Over 62S2 read 365A.
Departure 365'.
To find the difference of latitude.
Under 414A set 90S2.
Over 28S2 (comp. of 62°) read 194.5A.
D.Lat. 194'.5 or 3° 14'.5 S. (named S. because the tr.is S.).
(Note that both these problems can be solved together with one setting of the slide by moving the cursor from the course on scale S2 to the complement of the course, thus multiplying by the sine in the first case, and by the cosine in the second.)
To find the difference of longitude.
The middle latitude is obtained by applying half the D. Lat. found to the latitude of
the departure position. Thus the Mid. Lat. is 48° 53'.
Under 365A set 41° 07'52 (comp. mid. lat.).
Over 90S2 read 556A.
D.Long. 556' or 9° 16' W. (named W. because the tr. is W.). The D.R.
position is therefore lat. 47° 15'.5 N. Long. 18° 36' W.
This process of calculating the D.R. position is very useful when changing from one chart to another, especially if the charts are of a different scale, or when greater accuracy is required than can be obtained by measuring a long distance run on a chart with a varying scale of latitude. If it is desired, the course and airspeed of the aircraft can be used to calculate an air position. When the geographical position is required the wind velocity is applied as an additional track and distance. This "track" will represent the direction of the wind (downwind), and the distance will be the distance the aircraft has been blown downwind, during the time of flight at the given wind speed.
The use of pre-computed lines of position.
When a long flight is being carried out above layers of clouds, or over the high seas, and astronomical navigation is being employed, it is very convenient sometimes to compute the calculated altitude before the observed altitude is taken. This saves time if course has to be altered as a result of the observation made, and it enables most of the work to be done when the navigator is fresh and not flurried.
Knowledge of the estimated track and ground speed of the aircraft will enable its D.R. position to be plotted for every hour or half-hour of the flight. Using these positions and the G.M.T. of each E.T.A., calculate the individual altitudes of the chosen heavenly body.
When in flight, and the time approaches for the first observation, take the series of
sights as near as possible to the G.M.T. which was used for the calculated altitudes. The
pre-computed altitude can be corrected for any slight difference of time by the following
formula:
Correction = cos lat. x sin az. x diff. in secs. / 4
Example: Pre-calculated altitude 36° 47', azimuth 5. 47° W. G.M.T. 15 hrs. 06 mins. 00
secs. D.R. lat. 48° N. G.M.T. of observation 15 hrs. 07 mins. 06 secs. Obs.alt. 36° 23'.
Difference 66 secs.
Under 42S1 set 90S2.
Move X to 47S2.
Set 90S2 to X.
Move X to 66B.
Set 40B to X.
Over l00B read 8.1A.
The correction to pre-computed altitude is 8.1 minutes. As the hour angle is westerly, the body is decreasing in altitude. The correction is therefore subtracted and the calculated altitude to use is 36° 39' and the intercept will be 16 miles away.
The fix by horizontal angles.
The horizontal angle between two points results in a circle of position, the radius of which is obtained by the formula:
.5d / sin q
where d = the distance between the points and q = the horizontal angle.
The intersection of two circles of position will give the position of the observer.
Although this problem can be solved by using a station pointer or a protractor, these instruments are not always convenient to use on all charts. By using the slide rule to solve the problem of finding the radii of the circles of position, and determining the centres of these circles by construction, an accurate and simple method is always at hand.
Example: A and B are two objects 6 miles apart, and C a third object 8.6 miles from B.
The horizontal angle between A and B is 68° and between B and C 56°. Required the radii
of the two circles of position.
Under 68S1 set 6B.
Under 5A read 3.23B.
Under S6S1 set 8.6B.
Under 5A read 5.19B.
The respective radii are 3.23 and 5.19 miles respectively. Arcs made, using each pair of
objects, and the radius applicable will determine the centres of the required circles of
position, and the intersection of arcs from these centres will give the position of the
observer.
Although a fix by this method is not very practicable when airborne, it is invaluable when a survey of an advanced landing-ground or anchorage is being carried out.
To find conversion angle.
Formula:
½ D. long. x sin mid. lat. = conversion angle.
D.long. 6° 40'. Mid. lat. 62°.
Under 6° 40' S1 set 90S2.
Move X to 62S2.
Set 90S2 to X.
Over SB read 2° 56' S1.
Conversion angle = 2° 56'.
Numerous rules have been proposed which are purported to aid the navigator in remembering how conversion angle should be applied. If it is remembered that no matter whether the latitude is North or South, or whether the bearing is from a shore station or from the aircraft, the conversion angle correction is always applied towards the Equator, no difficulty will be encountered.
Radius of action.
The problem of finding the radius of action of an aircraft along a given track for a
known endurance is a very simple matter if the slide rule is always employed. Formula:
(G/S out x G/S home) / (G/S out + G/S home) x fuel hours = radius of
action.
Example: Airspeed 230 m.p.h. Track out 040° T. Wind velocity 20 m.p.h. from 102° T.
Fuel hours 35.
Wind is 62° on the bow.
Set X to 230A. 62S2 to X. X to 20A.
Under X in S2 read 4½° (drift).
Over 57½ S2 read 220A = G/S out (against wind).
Over 66½ S2 read 239A = G/S home (with wind)
220 + 239 = 459.
To 22D set 1C. X to 239C. 459C to X.
Read in D under 35C radius of action, 4010 nautical miles.
The time to turn is found from the time required to fly the 4010 miles at the outward G/S.
To find the error in track from a position line parallel to the D.R.track.
When navigating by astronomical observations, every advantage should be taken to observe heavenly bodies abeam of the aircraft, as the resulting position lines will give a good indication of the true track of the plane.
If no terrestrial observations have been possible since the departure, it will be desired to know the error in the course being steered. This can be easily found as follows.
Example: After flying 186 miles an observer obtained a position line placing the
aircraft .38 miles to starboard of the D.R. track. Find the error in the track.
Over 38D set 186C.
Under 1C read 11½T1.
The Track error is 11½°.
This method can also be employed when navigating over land, or when D/F W/T bearings are being used. It can also be used to give the alteration of course required to reach a certain destination, when of course the distance of the aircraft from the destination should be used instead of the distance run since departure.
It might be noted here that when sights are being taken to make a running fix, a sight of a heavenly body on the beam should invariably be taken first, as it will not then be necessary to transfer this position line for the "run" between it and the next observation. It will be found sufficiently accurate in practice to extend the position line until it cuts the line resulting from the second sight, thus giving a fix and saving one the labour of transferring the observation for the time interval between sights.
Correction of refraction.
Altitudes above 8°. Multiply the cotangent of the altitude by .96.
Altitude 36°, required the correction for refraction.
Over 36T1 set 96C.
Over 1 D read 1.3 C (to nearest first place of decimals).
Correction is 1.3 minutes minus to the apparent altitude.
Correction for dip of the sea horizon.
Formula: ÖHeight x .98.
Example: An observer flying at 840 ft. above sea-level requires the dip correction.
Set X to 840A.
Set 10C to X.
Under 98C read 284D.
Dip Correction is 28.4 minutes minus to the observed altitude.
To find the distance to the sea horizon.
Formula: Ö height x 1.15. The resulting distance is given in
nautical miles.
To find the distance of an object from the angle of depression.
For distances up to ten miles.
Formula: .565 H / q = distance in nautical miles = D1.
H = height of observer in feet above the object.
q = angle of depression in minutes.
For distances over ten miles or for greater accuracy.
Formula: .565 H / (q - .4D1) = D2.
D1 and D2 = distances in nautical miles.
D1 should be found, using the first formula, and then when .4D1 is
obtained the second formula can be used to calculate the final result.
To find D1.
Over 565D set q in scale C.
Under H in scale C read D1 in scale D.
Evaluate q - .4D1.
To find D2.
Over 565D set q - .4D1 in
scale C.
Under H in scale C read D2 in scale D.
© Hodder Stoughton, reproduced with permission.