| Slide rules HOME page | INSTRUCTIONS | CONTENTS |
SECTION SIX
LOG-LOG SCALES
Evaluation of Powers and Roots - Common Logarithms - Natural Logarithms.
ASSOCIATED with slide rules, we occasionally see quite unfamiliar scales which have been evolved for special purposes by people who have many calculations of a peculiar nature to make. If a complete collection of such special scales could be made, it would, no doubt, furnish an interesting study, and occasion surprise on account of its diversity.
Log-log scales are less frequently used than the scales we have so far studied, but they are not in any sense "special" scales. Many people who have possessed a slide rule for years are not familiar with log-log scales, since these are not included in the scale equipment of the standard slide rule.
Popular models of inexpensive slide rules sold in large quantities in this country include log-log scales, and as there are now a very large number of these rules in use, it may be assumed that the use of the log-log scales is extending. Apart from considerations of utility, the inclusion of log-log scales adds to the pleasure which may be derived from the use of a slide rule.
In Section 13 we shall see that in order to raise a quantity to a power or to extract a root we must look out the logarithm of the quantity, then multiply by the index, and so obtain the logarithm of the result. The evaluation of 5.61.8 involves finding the log of 5.6, multiplying it by 1.8. This gives the log of the answer, i.e. (log 5.6) x 1.8 = log of answer. We cannot perform these operations entirely with the ordinary scales, since we must consult a table of logarithms. (It is true that if a slide rule is equipped with a log scale - which must not be confused with the log-log scale - we can find the log of a quantity, and after multiplying by the index, find the anti-log of the product, and so obtain the result. Regarded from a practical standpoint, the slide rule is used to save time, and on these grounds there is nothing to be gained by using the log scale in preference to a table of logs; the latter is certainly more accurate.)
If we have a means of finding the log of (log 5.6) we can proceed thus: log (log 5.6) + log 1.8 = log (log answer).
As its name signifies, the log-log scale is designed so that its graduations represent values of the logarithms of logarithms of numbers; the graduations of the ordinary scale represent logarithms of numbers.
It is important to understand that the numbers marked along a log-log scale cannot be varied. We know that the 2 in the C or D scales may be used as 2 or 20 or 2000 or .0002, but the number 2 in the log-log scale can have no other value except 2. The reader will, therefore, realise that the range of the log-log scale selected for use in any rule is fixed and limited. It is for the designer of the slide rule to decide what is the best range to include in any particular type of rule.

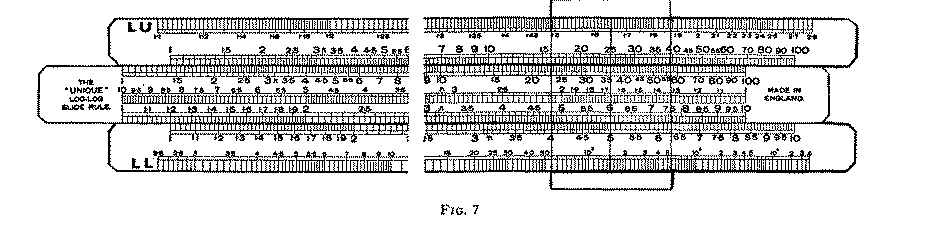
The log-log scale frequently lies along the top and bottom edges of the face of the stock, and if the reader will examine Fig. 7 he will see that the scale lying along the upper edge of the stock starts at 1.1 and finishes at 2.9. The lower scale starts at 2.6 and finishes at 40,000. These two scales are, in fact, one scale only, divided into two parts. The upper portion should be regarded as the part of the complete scale lying in front of the lower section. There are small overlaps on both scales. Strictly speaking, the upper scale finishes at 2.7183, immediately above l0D, and the lower starts at the same value directly under 1D. The log-log scale is used in conjunction with scale C.
As we have said, the limits of the complete scale can be varied, and you may find that the scales of your slide rule, assuming it has a log-log scale, may be different from the one shown in Fig. 7. In some rules you may find more than two sections of log-log scales, but whatever type of rule you possess the examples given below are typical of the calculations which can be made with it.
Evaluation of Powers and Roots
The most useful feature associated with the log-log scale is the ease with which all powers and roots can be calculated. (Abbreviations LU and LL = Upper and Lower log-log scales, respectively.)
Example: Evaluate (i) 6.42.7 and (ii) 2.7Ö 6.4.
(i) To 6.4 LL set 1C. X to 2.7C.
Result under X in LL = 150.
(ii) To 6.4 LL set 2.7C. X to 10C.
Result under X in LU = 1.99.
Example: Evaluate 6.4 -2.7.
6.4 -2.7 = 1 / 6.42.7 = 1/ 150 (From Ex.
(i) above) = .00667.
Problem 21. Evaluate 21.51.66; 1.66Ö21.5; 21.5-1.66.
Example: Evaluate (i) 214.5; (ii) 9Ö 2 .
If the reader will attempt to effect these evaluations by the methods adopted in the preceding examples, he will find the answers "off the scale", in both cases. Result can be found quite easily as now shown.
(i) 214.5 = 74.5 x 34.5 (or the factors
2.1 and 10 might be taken)
= 6300 x 140 (evaluate separately as first example)
= 882000 (multiplication by C and D scales)
(ii) 9Ö2= 9Ö20 / 9Ö 10 = 1.395 / 1.292 = 1.08.
In this example the reader will find that when the 20 is found in LL and 9C is brought into coincidence with it, the 1C index is off the LL scale. If he imagines the LU scale to lie in front of the LL scale, he will see that 1C would then be directly over 1.395 LU. Actually, the 1.395 LU is found, using X directly over 10C, since in effect we have moved the LU scale from its imaginary position in front of the LL scale a distance to the right equal to the length of the C scale, i.e. 10".
Problem 22. Evaluate 1.280 and 3Ö1.2.
The log-log scale gives a means of finding common logarithms. Using X, set 1 of C to 10 in LL and project with X, the number whose log is required, from LU or LL into scale C. The logarithm so found will be complete with characteristic and mantissa. When 10 of C is set to l0LL the result obtained is 10 times the true figure.
Example: Find the common log of 150.
Set 1C to l0LL.
Above 150 in LL read in C 2.178.
Example: Find the common log of 3.
Set l0C to l0LL.
Above 3 in LL read in C 4.77, one tenth of which is 0.477.
The reader will see that the logs to any base may be found in a similar way. The 1C or l0C being set to the base in LL or LU.
If the reader will examine Fig. 7 he will see that the 1 of D lies immediately above 2.7183 (the base of the Naperian system of logarithms) in LL. The scales are positioned so that the natural or Naperian logs of all numbers in the log-log scales appear directly opposite in D. When projecting from LU, however, the result obtained is 10 times the true figure.
Example: Find the natural logs of 1.8 and 250.
Use X to project from 1.8 in LU, and 250 in LL into scale D.
Logs so found are .588 and 5.51.
We do not recommend that logarithms should be found as above except when other means of finding them are not to hand. Logarithms should be taken from tables. Naperian logs are derived from common logs by multiplying by 2.303.
The tenth powers of all numbers in LU lie immediately below in LL, and the tenth roots of all numbers in LL lie directly above in LU. The reader will appreciate these facts if he remembers that LU and LL together form one continuous scale with LU preceding LL.
Example: Find the tenth power of 21.
21 lies in LL, but 2.1 is in LU, and we can use 2.1 x 10, and raise
each factor to the tenth power.
Projecting 2.1 from LU to LL we obtain 1670, and the result, therefore,
is 1670 x 1010.
Example: Find the tenth root of 200.
Set X to 200 in LL. Read in LU 1.7.
Problem 23. Evaluate 3.210 and 10Ö13
We do not suggest that tenth powers and roots are likely to be required often in practical work.
Since we can use the log-log scales to evaluate all powers and roots, we can find square roots and cube roots by the same means, and frequently with a higher degree of accuracy than when using the A and D scales. The reader will now understand our contention that the A and B scales are of little value in a slide rule equipped with a log-log scale.
Example: Find the square root of 1.28 using (i) scales A and D; (ii) log-log scale.
(i) Use X or the index lines of the slide to project 1.28A into scale
D. The result appears to be a shade greater than 1.13.
(ii) Set X to 1.28LU, 2C to X, X to 1C. Result 1.1313 under X in LU.
The reader will find scope for the display of his ingenuity in obtaining results which cannot be directly taken from the log-log scales, and we think he will find a good deal of pleasure in using a slide rule equipped with these scales. (Several examples, which involve the use of log-log scales, appear in Section 16.)
The Dualistic rule and the Brighton rule which are dealt with in Sections 11 and 12 respectively are equipped with three-section log-log scales which are carried on the reverse of the slides. The additional sections of these scales increase the range from 1.01 to 40,000 as against 1.1 to 40,000 of the two-section LL scales.
If the reader has comprehended the explanation given above in respect of log-log calculations, he will have no difficulty with a slide rule which has its LL scale on the back of the slide. He will find an explanatory note, under reference log-log scales, in Section 11.
© Hodder Stoughton, reproduced with permission.