SECTION FIVE

A AND B SCALES

Squares and Square Roots - Cubes and Cube Roots - Cube Scale.

WITHOUT doubt the most frequently used scales of the standard slide rule are the C and D scales we have just studied, and we might, with justification, say that these are the most important scales in our slide rule equipment. It is impossible to say which scales stand next in importance. It depends upon the nature of the work to be done; if trigonometrical problems loom prominently in our work, then the sin and tan scales will frequently be used. Work of a different nature may demand frequent recourse to the log-log scale, and again electrical or commercial calculations may bring into service scales particularly designed to deal with them.

The reader will notice that we do not suggest the A and B scales possess a high degree of priority in the scheme of things. We are of the opinion that these scales are of little importance and that others could, with advantage, be substituted for them.

Since, however, the large majority of slide rules are equipped with A and B scales, we must spend a little time in studying them.

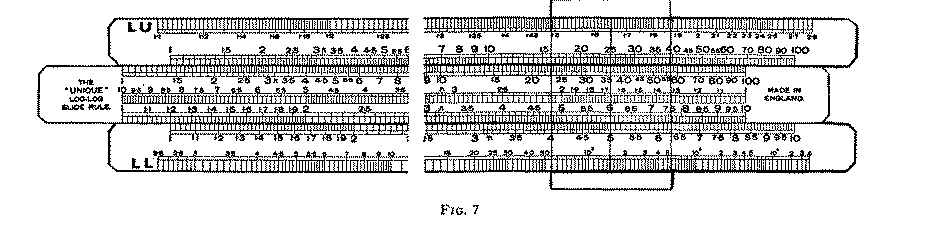
The A and B scales are adjacent to one another, the B scale lying along the top edge of the slide and the A scale on the stock. The reader will see them in Figs. 6 and 7. Each of these scales consists, so far as its graduations are concerned, of two identical halves, and we speak of the right-hand half, or the left-hand half, when we desire to make a distinction.

Scales A and B should carry 1 at the extreme left-hand end, 10 at the middle point where the two halves abut, and finish with 100 at the right-hand end, with the corresponding intermediate figures. In many slide rules the left-hand and right-hand halves are numbered exactly alike, with the figure 1 at the beginning and end of each half. Whilst this arrangement is not a great disadvantage to those familiar with slide rules, and expert in the use of them, we think the scale should be completely numbered as shown in Fig. 7. In subsequent notes we shall refer to the numbers as they are depicted in Fig. 7.

Each half of scales A or B is similar to scales C and D in as much as it is logarithmic. It is only half the length, and has only about half the graduations, and herein lies the disadvantage of using A and B for multiplication or division.

The reader is by now quite well aware that a slide rule will not give results with absolute accuracy. If we multiply together two numbers using ordinary arithmetical procedure we should obtain a result accurate to the last figure, but with a 10" slide rule we know that we can never be certain of the fourth figure and must often regard the third figure with suspicion. A 5" rule is less precise, and if one uses the A and B scales of a 10" rule for ordinary multiplication or division, he is in effect using a 5" rule. We have heard sarcastic criticism of the slide rule arising from the fact that results are not always completely accurate, but the thoughtful reader will, of course, realise that in our practical problems, the data we use are derived generally from measurements or observations which are susceptible to considerable error, in comparison with which the errors made in computation by slide rule are permissible.

We would, however, warn the reader carefully to consider whether the slide rule is likely to introduce errors which might seriously impair the result of some work or investigation he is pursuing. In the course of a chemical analysis, we might, using a good balance, determine the weight of a sample as 13·562 grammes, and we should be fairly certain that the last figure, the 2, was correct, and not 1 or 3. If this weight had to be multiplied by some other number which could equally be relied upon, we should hesitate at using a 10" slide rule, which might introduce an error many times as great as any error in the original figures. Some physical measurements can be made to a high degree of accuracy, and computations must, of course, be made with the same precision. When necessary we must discard the slide rule and use other means of reaching the result, but for most of our practical work the C and D scales of a 10" slide rule give results to an acceptable degree of accuracy.

When great accuracy of results is not important, and we are working to approximate figures, there is no harm in using scales A and B for multiplication and division, but we do ask the reader to avoid making this a practice, or soon he will find himself by habit using A and B when he should be working with C and D.

With very little modification, the instructions we have given in respect of scales C and D for multiplication and division apply to A and B. For scale D read A, for C read B, and remember that due to the duplication of the scales all the numbers in C and D appear twice in A and B, e.g. the 2 in C and D appears as 2 and 20 in A and B.

We have seen that when using C and D it occasionally happens that after carefully setting the slide we find that the next factor is "off the scale", and the slide has to be moved its own length and then re-set to obtain the required reading. When we use scales A and B, we find that if a factor in scale B is off the A scale at one end of the rule, the result can still be found by looking for the factor in the other half of scale B. It is possible to set the slide so that no result can be found. To avoid this, refrain from moving the slide so that more than half its length protrudes from the stock, remembering there are two alternative settings. Cultivate the habit, when setting the slide, of keeping it near the centre of the stock. It is natural to do this, and if persisted in for a time becomes a habit. We do not propose to say anything further concerning multiplication and division with scales A and B.

Squares and Square Roots

In Section 3 we mentioned that squares and square roots of numbers are easily obtained by using scales A and D in conjunction, and this, we suggest, is the most useful feature arising from the inclusion of scales A and B in our slide rule.

Immediately above any number in scale D appears its square in scale A. Look at your slide rule and you will find 4 in A over 2 in D, 9 in A over 3 in D, 25 in A over 5 in D, and similarly throughout the length of the scales. Conversely, the square roots of numbers in A lie directly below in D. When projecting from A to D or vice versa, we may use the cursor index line, or, if preferred, the index lines of the slide. The index lines of the slide are the end lines (excluding extensions if any), the 1 and 100 of scale B, and 1 and 10 of C. It will be clear that these lines give a means of striking across from A to D, and sometimes these are preferred to the cursor index, since there is no possibility of slight error due to parallax.

The student will find no difficulty in squaring numbers:

Example: Find the square of 4·55.
    Set X to 455D. Under X read 207 in A. Result 20·7.
If we use the slide to project across the rule, the procedure is:
    Set 10C to 455D. Read result 20·7 in A over 100B.

We shall, in subsequent notes, refer to X, the cursor index for projecting from A to D, but we advise the reader to use the slide when it is convenient to do so. In many calculations involving squares and square roots, the slide cannot be used for projecting across since it is required for other operations. In such cases the X must be employed.

Problem 16. Find the squares of 8·75 and 167.

Evaluation of square roots is the reverse operation and is just as easy, but there is one point we must mention in passing.

If using scales A and B we desire to multiply 2 by some other factor, we may use the 2 in the left-hand half of A, or the 20 in the right-hand half, taking the figure most convenient, but if we require the square root of 2, we may not use the 20. The reader will see that under 2 of A the reading in D is 1·414, whereas under 20 in A appears 4·47 in D. We know of no more prolific source of slide rule error than this one of using the wrong half of scale A when extracting square roots.

There should be no difficulty in finding the square root of any number lying between 1 and 100. We know the square roots of 1, 4, 9, 16, 25, 36, 49, 64, 81 and 100, and we should make no mistake with any number within this range.

Assume we require the square root of 45·2. We place X over 452 in the left-hand half of A and note the corresponding value in D; it is 213. The square root of 49 is 7 and our answer should be just less than 7. 213 does not agree, and we see immediately that we have in error taken the square root of 4·52, which is 2·13. If we move the cursor to 452 in the right- hand half of scale A we find the corresponding reading in D is 6·72; this is the square root of 45·2.

If the scales of your slide rule are comprehensively numbered as in Fig. 7, the problem of extracting square roots is simplified, as there will be no difficulty with numbers lying between 1 and 100. When extracting square roots, it is advisable to multiply or divide the original number by even powers of 10 to bring it into the range of 1 to 100, and after taking the square root, to make the necessary adjustment in the result.

Examples: Find the square roots of (i) 1462; (ii) ·0000227and (iii) ·000227.

(i) Ö1462 = Ö(14·62 x 100) = Ö14·62 x 10 = 3·82 x 10 = 38·2.

(ii) Starting with ·0000227, we tick off pairs of figures as shown ·00'00'22'7; we thus obtain 22·7 as the figure whose square root we must find on the slide rule. This root is 4·76, but we must now move the decimal point three places to the left to correct the alteration made when earlier we ticked off three pairs of figures to the right.
    Result is ·00476.

(iii) Ö·00'02'27
    Ö2·27 = 1·505
    Result ·01505.

We could give the reader other rules for the determination of position of decimal point in the root, but we are confident that the method we have adopted above is the best. It is easily understood, but because of its importance we will enumerate the steps:

(1) Examine the number whose square root is required. If it lies between 1 and 100 its square root will lie between 1 and 10. Find the number in A and project with X to D where the root will be found. Insert the decimal point to the right of the first figure of the result.

(2) If the number does not lie between 1 and 100 move the decimal point in steps of two figures at a time until the number falls in this range; now take the square root of the number so altered and insert the decimal point as at (1) above.

(3) Finally, move the decimal point in the result obtained at (2), one place for each step of two figures made when altering the number, moving in the opposite direction.

Problem 17. Find the square roots of 814, 8140, ·0166 and ·0000166.

Example: Calculate the volume of a cylinder 11 ·2" diameter, 19·6" long.
In terms of diameter d and length 1 the volume is (p/4) d²l.
    Set 1C to 112D, X to 196B, l0B to X.
    Result 193 in A above 785B. (.785 = p/4).
    Approximation 11 x 11 = 132. ¾ of 132 is near 100. 100 x 19·6 = 1960.
    Result 1930 cu. inches.
    To reduce the result to cu. feet:
    To 1930A set 1728B. Read 1115 in A above 1 (or 10) in B.
    Result 1·115 cu. feet.

The symbols c and c' which appear in some slide rules near the left-hand end and near the middle of the C scale are provided to assist in calculations involving volumes of cylinders. The special lines are termed gauge points; they are referred to in Section 15.

Problem 18. Calculate the diameter of a pipe which will discharge 3 cu. ft. of water per second at a rate of flow of 8 ft. per sec.

There are methods of finding square roots without using scales A and B. We used one in the example preceding Problem 4. Other methods will be mentioned in the sections dealing with log-log and reciprocal scales.

Cubes and Cube Roots

To find the cube of any number set the 1 or 10 of scale C to the number in D. Above the number in B read the cube in A.

Example: Find the cube of 244.
    Set 1C to 244D. Over 244 in B read in A the cube which is 145. Insert the decimal point by inspection, making the answer 14·5.

There are rules which may be used for the determination of the position of the decimal point in the result, but they are confusing, and we cannot recommend the reader to use them. It is simpler to obtain an approximate result.

Problem 19. Cube 16·8.

Cube roots may be extracted by several different methods using scales A, B, C and D. The method we now describe is, we think, the best.

When extracting square roots we converted the number whose root was required to one lying between 1 and 100. In the case of cube roots we step off figures, in groups of three, until the number whose cube root we are finding lies between 1 and 1000. The cube root will then lie between 1 and 10.

The slide rule manipulation is as follows:
    Place the cursor index X over the original number in scale A.
    Adjust the slide so that the number in scale B under X is exactly the same as the number in D opposite 1 (or 10) of C.
    The number so found is the cube root.

If the reader will use his slide rule and set X over 8 in A he will find that when the slide is set so that 2B lies under X, 2D will be opposite 1C; 2 being the cube root of 8.

If the number whose cube root is sought lies between 1 and 100, use the appropriate reading in scale A for setting X, but if the original number lies between 100 and 1000, select it in the left-hand half of A, which, for our present purpose must be regarded as a continuation of the A scale and stretching from 100 to 1000.

These instructions may seem rather complicated, but if the reader will take his slide rule to find the cube roots of say, 6, 60 and 600, using the 6 in the left-hand part of scale A for the 6 and 600, and the right-hand half of the scale for the 60, he will find no difficulty in reading the three roots, 1·82 in D under 1C, 3·91 in D under 1C and 8·44 in D under 10C. In extracting cube roots it helps considerably in setting the slide if a mental estimation of the root is made. If we require the cube root of 450, we try, say, 6. 6 x 6 = 36, which we call 40; now 6 x 40 = 240, and this is well below 450. Try 7; 7 squared is 49, say 50, and 7 x 50 = 350. Still too small, so try 8. 8 x 8 = 64; and 8 x 60 = 480. We have passed the 450, so our cube root lies between figures 7 and 8. We there fore set X to 45 in the right-hand part of scale A and our slide so that 10 in C is near 8D, and if we now move the slide slowly to the left we shall find that when 10C is over 7·66D, X is over 7·66B. \³Ö450 = 7·66.

Example: Find the cube root of ·000'012'64.

First move the decimal point to the right in steps of three figures, as shown by the ticks, until a number lying between 1 and 1000 is found. This number is 12·64. The cube root of 12 is between 2 and 3. Set X to 12·64 in A. Set 1C to 2D. Now move the slide to the right. When 1C reaches 233D, 233B will be under X. The cube root of 12·64 is 2·33, but we must now move the decimal point two places to the left to compensate for the stepping off of two groups of figures in the original number. The required cube root is .0233.

Problem 20. Find the cube roots of 8, 80, 800, 9481, .0213 and ·00046.

Cube Scale

Slide rules equipped with a special scale for evaluating cubes and cube roots of numbers are available. Unless the reader is concerned with work which involves the necessity of frequently finding cubes or cube roots - we cannot think of any work which does - he will find little use for the scale. The cube scale usually lies along the top or bottom edge of the face of the stock, and if the reader will inspect it, he will see that the complete scale is made up of three identical scales placed end to end. Each of these three parts is one-third of the length of the C or D scales, and is divided logarithmically. The left-hand third of the scale starts at 1 and finishes at 10, the middle third stretches from 10 to 100 and the right-hand third from 100 to 1000.

To cube a number it is only necessary to project it from scale D to the cube scale, and cube roots are found by projecting numbers from the cube scale to the D scale.

After reading the instructions we have given for extracting cube roots by the A, B, C and D scales, the reader should have no difficulty when he is using a rule with a scale of cubes.

The stepping off of groups of three figures to bring the original number within the limits of 1 and 1000 should be effected. This makes it easy to select the number in the appropriate section of the cube scale. After the cube root is found in D the adjustment of the position of the decimal point follows the rules we have given earlier.

© Hodder Stoughton, reproduced with permission.