| Slide rules HOME page | INSTRUCTIONS | CONTENTS |
SECTION FOUR
C AND D SCALES
Multiplication - Division - Multiplication and Division combined - Position of a Decimal Point.
IN this section appears the first examples involving the aid of a slide rule. In the condensed instructions, we shall adopt abbreviations, namely: C for scale C; D for scale D; 12C means line 12 in scale C; X refers to the index line of the cursor.
Examples are worked to assist the student. Problems are inserted for the student to solve. Answers to problems are given at the end of the book.
This section is devoted to those operations most often effected by slide rules; those which every student must first learn, multiplication and division.
We have in Section 3 advised the reader to refrain from using scales A and B for multiplication and division, and we shall confine our attention to scales C and D. Throughout this section no mention will be made of the other scales, which, for the time being, you may ignore.

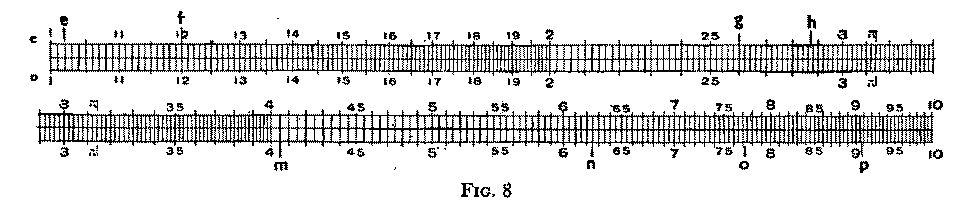
Scales C and D are subdivided in decimals, and we must now assume that you are able to read them without difficulty. Fig. 8 illustrates the C and D scales as you should find them in practically all 10" rules. In order to illustrate them full size, we show in the upper part the left-hand half, and in the lower part the right-hand half of the scales. to show the scales complete in one length would necessitate them being reduced in size in order to print them on a page of this book; this would make some of the divisions inconveniently small and difficult to read.
Problem 9. You are asked to read the positions of the lines marked in Fig. 8 and compare your reading with those we give in the answers to problems. If you feel confident that you are able to read the scales we can safely proceed. If you have any difficulty we ask you to turn back to Section 1 and study that part dealing with reading scales, or better, to enlist the aid of someone conversant with scales. A few minutes of oral explanation will assist more than pages of written notes which would be too tedious to be endured.
Let us examine these four simple examples:
12 x 32 =384
1.2 x 3.2 = 3.84
.012 x .032 = .000384
120 x 320 = 38400
In every case, if we ignore the position of the decimal point and the noughts which precede or follow the significant figures, we are concerned only with the multiplication of 12 x 32. You will notice that the answer in each case has only the three significant figures, 384. If we use a slide rule to carry out these four multiplications the operations would be identical.
The line marked f in Fig. 8 is drawn to coincide with the 1 .2 graduation. In some rules this line may be marked 2, and if such is the case, you will be using a rule with the abbreviated marking to which we have referred earlier. Try to secure a rule in which the C and D scales are numbered as in Fig. 8.
1.2 graduation may, for our purpose, be read as 1.2, or 12, or .012, or 120, or any combination of figures in which 12 stand together followed or preceded by any number of noughts. If, however, we read this line as 102 we shall be making a fundamental error, and our result would be incorrect. You will, no doubt, have found the line 1.02 in connection with Problem 9. It is the line marked e.
We will now see how the result 384 is derived from the two factors 12 and 32. You will understand that we are dealing with simple numbers for the purpose of instruction. Obviously there is no other point in using a slide rule to compute results which could easily be obtained without its aid.
If at any time you are in doubt as to whether you are using your slide rule correctly, always work out an elementary example with simple figures, so that you can check the slide rule result. We tender this advice more particularly when complicated examples may arise, or when the reader is using scales which he seldom needs.
Example: Multiply 12 by 32.
Find 12 in scale D, move the slide to the right to bring the 1 of scale C coincident with the 12 of scale D. Directly under the 32 in scale C you will find the result, 384, in scale D.
We have described the two operations fully, but we repeat them below in the condensed form we shall hereafter use. If you will get familiar with the condensed form, you will find it much less tedious to follow than a wordy description, and typography is reduced. The description started by saying, find the 12 in scale D. You may just note the 12 in scale D by eye, or, if you prefer it, place the cursor index over it. If the cursor is used, an additional mechanical operation is involved, but we think it is the easier method to adopt; this is a matter of opinion, and you may please yourself. We shall make no reference to using the cursor for picking up the first or final readings.
In the condensed form the operations would be: Set 1C to 12D. Under 32C read result, 384, in D.
If we had been multiplying 32 by 10 the answer would have been 320. Our answer must be rather greater than 320 since we are really multiplying by 12, and we, therefore, write it as 384. The answer could not be 38.4, nor could it be 3840. We hope you will understand that having obtained the figures 384 from our slide rule, we must determine the "order" of the result, or, in other words, find the position of the decimal point.
Example: Find the area in square inches of a rectangular sheet of paper measuring
4.8" x 6.4".
Set l0C to 48D. Under 64C read 307 in D.
Position of the decimal point is determined by inspection of the two factors. We obtain an approximate answer by taking the factors as 5 and 6; in doing this you will notice that we have increased 4.8 to 5 and reduced 6.4 to 6. The product of 5 times 6 = 30 must be fairly near the true result, and we may, therefore, insert the decimal point, making our answer 30.7 sq. in.
There are other methods of determining the position of the decimal point, but we think at this stage you would find them very difficult to understand. We mention them at the end of this section, but we advise you always to adopt the approximation method of finding the position of the decimal point.
In the example 4.8 x 6.4 you will notice that if we set the 1 of C to 48 of D, then the 64 of C is "off the scale of D", and we must move the slide to bring the 10 of C to coincide with the 48 of D to obtain a reading. The necessity of re-setting the slide does sometimes occur when we are using scales C and D, but when we have a little experience of using a slide rule, we seem to acquire an instinct which warns us when we are using the wrong end of scale C. When setting the 1 or 10 of C, you should move the slide roughly into position and then take a quick glance at the factor in C which you wish to use. If this factor lies over some part of scale D you can proceed accurately to adjust the slide and obtain your result. Occasionally the factor in C is only slightly outside the scale of D. If you will examine Fig. 9 in Section 7, you will find there are a few graduation lines on the left-hand side of the 1 of scale C and D, and also a few graduations on the right-hand of the 10 of these scales. These extensions of the scales are sometimes useful for picking up a result which otherwise would be just off the scale. You will no doubt notice that the graduations to the right of the 10 are identical with those immediately to the right of the 1, and those which lie to the left of the 1 are the same as those which precede the 10. These extensions are short additions of the C and D scales.
Example: Calculate the weight of a cast-iron plate 40 ½" long x 28.7" wide x 5/8" thick. (1 cu. in. of C.I. weighs .26 lb.)
We have four factors to evaluate. 40.5 x 28.7 x .625 x .26.
Set l0C to 405D. X to 287C. 1C to X. X to 625 C. l0C to X.
Result 189D under 26C.
Approximation: .26 is slightly more than 1/4, and 1/4 of 40 is 10. 5/8 of 28 is somewhere
near 18. 10 times 18 = 180. The answer must be 189.0 lb. weight. (The positions of the
four necessary readings are marked in Fig. 8 to assist those who may still have difficulty
in reading the scale.)
You are now requested to repeat the foregoing example by taking the factors in different orders. Start say with the 5.8 and multiply by 40 ½, then by .26, and finally by 28.7. The result should be the same irrespective of the order in which the factors are selected. With four factors there are possible 24 different sequences in which the operation of multiplication may be effected, and we think it is an excellent exercise for the reader who is just becoming familiar with the slide rule to work through a few of these sequences. 1891 should result from every attempt, and it is a matter of interest to see how little variation there is in the results obtained by taking the factors in different orders. With a little care the reader will find the correct result emerging time after time.
The student may like to know how the 24 sequences referred to are derived. Let us for ease of expression denote the four factors by the letters a, b, c and d. Here are six different sequences, a x b x c x d, a x b x d x c, a x c x b x d, a x c x d x b, a x d x b x c, a x d x c x b. Each of these six starts with a. Now there are six others each starting with b, and similarly six commencing with c and with d. You will, no doubt, be able to complete the whole of the series without difficulty. We are not suggesting the example need be solved in all 24 ways, but to carry out a few will serve as good practice.
Problem 10. A rectangular water tank has dimensions 2' 3" x 18" x 4' 6". Calculate the weight of water this tank will contain when it is three-quarters full. (1 cu. ft. of water weighs 62.3 lb.)
Example: Calculate the area of a circle 2.8" radius. (If r is the radius of a circle, and d its diameter, then area = p r2 = p d2 / 4. p, pronounced pi, is the Greek letter which is always used to denote the value 3.14. It is the ratio of circumference to diameter of a circle, and it enters into all our calculations concerning circles, spheres and other associated forms. p is generally denoted by a special "gauge mark" in scales C and D, see Fig. 8.)
Area = pr(2.8)2 = p x
2.8 x 2.8.
Set 1C to 28D. X to 28C. l0C to X. Result 246 in D under p in C.
Approximation: 3 x 3 x 3 = 27. Result is 24.6 sq. in.
Problem 11. Calculate the volume of a cylinder 8.2" radius and 12.6" long. (Volume = ( pr2) L.)
If you have now understood the rules for multiplication of two or more factors, you should have no difficulty in using your slide rule for dividing. We will, however, consider a few examples in order to make sure. If your rule is set to multiply together two numbers, then it is also set for division. Will you adjust the slide so that the 1 in scale C is coincident with 2.5 of scale D. Immediately under the .3 of C you will find 7.5 in D. This setting of the slide enables us to multiply 2.5 by 3. Now, working backwards from this result, we see that in order to divide 7.5 by 3, we need only adjust the slide to bring the 3 of scale C opposite the 7.5 of scale D; exactly under the 1 of C we find the 2.5 of D and we have effected the division of 7.5 by 3 and obtained the result 2.5.
We repeat our advice, if in doubt concerning method, work out an easy case with simple figures so that a mental check can be obtained easily, such as the following:
Example: How long will it take a man walking at the rate of 4 miles an hour to cover 14 miles? to 14D set 4C; under l0C read 35D; the answer is, therefore, 3.5 hours.
Please note that henceforward we shall often write the significant figures to be selected in the scales without inserting the decimal points. In the example above the numbers 14 and 35 in scale D are those marked 1.4 and 3.5. We hope by now the reader has appreciated that we take no notice of the positions of the decimal points in the various numbers while we are manipulating the slide rule. When we have obtained a numerical result we insert the decimal point by inspection if the numbers are simple; if the numbers are too complicated to allow of a mental approximation to be made, we shall write them down, then simplify and cancel them sufficiently to enable us to obtain an approximate result.
Example: Find the radius of a circle which has an area of 161 sq. ft.
Now pr2 = 161. r2
= 161 /p
Set p in C to 161 in D. Under l0C read 512. Insert decimal
point by inspection giving 51.2 = r2. To obtain the radius we must find the
square root of 51 .2. There are several ways of finding square roots by slide rule, but
remember we are restricted in this section to the use of scales C and D only. We can
easily obtain our result: Place X over 51 .2 in D and move the slide to bring 7 in C under
X. (7 x 7 = 49,and it is clear that our square root is a little greater than 7.) Now move
the slide slowly to the left until the reading in C under X is the same as the reading in
D under the 10 in C. We make the answer 7.15.
You will see that our endeavour has been to set the slide so that we are multiplying a number by itself and obtaining 51 .2 as the result. Please study very carefully this method of obtaining square root.
Problem 12. A sample of coal weighing 13.4 grammes, on analysis was found to contain 9.6 grammes of carbon. Calculate the percentage of carbon contained in the sample.
Example: Find the value of 182 / (6.2 x 808 x .029)
to 182D set 62C; X to 10C; 808C to X; X to 10C; 29C to X. Answer 1252 in D under 1C.
To find position of decimal point we may write the expression in a simpler form 182 / (6.2 x 8.08 x 2.9); you will notice that we have moved the decimal point in the 808 two places to the left. This is equivalent to dividing 808 by 100 and reducing it to 8.08. At the same time we have multiplied the .029 by 100 by moving the decimal point two places to the right. Now, in an expression such as we are dealing with, we do not alter its numerical value if we multiply and divide the denominator (or numerator) by 100, or any other number, but by this device we alter the terms of the expression in such a manner that we can more easily see the order of the result. If you now look at the denominator you will see that we have approximately 6 x 8 = 48, and 48 x 2.9 is somewhat less than 150. 150 divided into 182 is clearly greater than 1 and less than 2. Our result is, therefore, 1.252.
Multiplication and Division Combined
Frequently calculations involve a combination of multiplication and division. We shall find that our slide rule is particularly well designed to cope with them.
First consider the simple case (8 x 3) / 4 . We can easily obtain the answer mentally as 6. Using the slide rule we might multiply 8 by 3 and then divide by 4. Alternatively, we might divide the 8 by 4 and then multiply by 3. The answer would be 6 by either method, but we shall find that there are less slide rule operations if we adopt the second.
By first method: Set l0C to 8D, X to 3C, 4C to X, under l0C read answer 6 in D.
Second method: Set 4C to 8D under 3C read answer 6 in D.
The first method involves us in four slide rule operations, whereas the second method demands only two. You are particularly advised to cultivate the habit of using the second method in all calculations which involve combined multiplications and division. Compared with the first method you will in general reduce the number of operations by about one-half, and you will often be nearer the exact result.
A little thought will show how the saving is effected. Please set your rule so that 4C is over 8D. This is the setting for dividing 8 by 4 and the answer, 2, is in D immediately under 1 in C. Now, to multiply 2 by 3 we must set the 1 of C to the 2 of D and read the answer, 6, in D under the 3 in C. We find, however, that having set the slide for dividing 8 by 4, we have also, with the same setting, prepared for the multiplication of 2 by 3. We do not even take the trouble to read the intermediate answer, 2, but go direct to the final one, 6.
Example: A farmer is asked to make for a Government Department a return showing, as percentages, the acreages he has under wheat, oats, barley, root crops, grass and fallow. After check up he finds that he has sown wheat 37 ½ acres, oats 29 acres, barley 17 ½ acres, root crops 42 acres, has grass 19 ½ acres and lying fallow 7 ½ acres. total acreage is 153.
We could divide each of the separate acreages by 153 and so obtain the percentages, but we find it much easier first to divide 1 by 153 and then effect the multiplications with one setting of the rule.
Set 153C to 1D.
| Under 37 ½ C | read in D | 24.5% wheat |
| ,, 29 C | ,, |
19.0% oats |
| ,, l7 ½C | ,, |
11.5% barley |
| ,, 42 C | ,, |
27.5% roots |
| ,, l9 ½C | ,, |
12.8% grass |
| ,, 7 ½C | ,, |
4.9% fallow |
| total | 100.2% |
If we have made our calculations correctly, the total of the crop percentages will be
100%. As you see, our individual percentages give 100.2% as the total. The slight
discrepancy is due to the small errors we make when using a slide rule, but the total is
so close to 100% that we may assume we have made no error of importance and we need not
check through the calculations. If you try to read the percentages to the second place of
decimals you will probably get results which are even nearer to the 100%, but it is futile
to express your slide rule result to a degree of accuracy greater than that of the
original data. It is quite certain that the farmer's estimation of acreage under the
different crops will contain errors much greater than 2 in 1000.
We think the foregoing example gives excellent practice, and we give a similar one for the reader to work through.
Problem 13. The manufacturing costs of a certain article were estimated as follows: Direct Labour £68. Drawing Office £6. Materials £91. Works Overheads £4 l0s. 0d. General Office Overheads £3 l0s. 0d. Express these items as percentages of the total cost.
We will finish this dissertation with a typical example of combined multiplication and division, since this type of problem arises very frequently in the course of practical work.
Example: 8.2 x 14.7 x 29.1 x 77.6 x 50.2 / (18.6 x 32.7 x .606 x 480)
Set X to 82D, 186C to X, X to 147C, 327C to X, X to 291C, 606C to X, X to 776C, 480C to
X, X to 502C.
Read the result 772 in D under X.
Approximation gives 70; therefore, result is 77.2.
We have stated earlier in this section that we would give rules for the determination of decimal points in numerical results. In many cases the positions of decimal points are known from the nature of the problem; in many others the decimal point may be inserted by making mentally rough approximations. In cases in which the figures are numerous and diverse so that it is unsafe to attempt to approximate mentally, the data should be written down in round numbers and then reduced to simple forms by cancellation and other means, so that approximation can be made.
Our advice to the reader always to fix the position of decimal points by inspection or approximation is, we believe, quite sound; in the course of a long acquaintance with slide rules and users of slide rules, we have met only one individual who consistently adopted any other method.
Digits
When we speak of the number of digits in a factor we refer to the number of figures lying
before the decimal point when the factor is 1 or more. When the factor is less than 1, the
number of digits is the number of noughts immediately following the decimal point, and
this number of digits is negative. In the following factors given as examples, the numbers
of digits are given in brackets: 6 (1); 81(2); 508 (3); .45 (0); .026 (-1); .0048 (-2);
.0007 (-3).
Rule for Multiplication
Please set your rule for multiplying 3 by 4. The result is 12, and the slide is protruding
at the left-hand end of the stock. In this example the number of digits in the product is
2, which is equal to the sum of the digits of the two factors which contain one each.
The following examples in which 3 and 4 are the significant figures show how the index
rule works. In each case you will see the sum of the digits (which are shown in brackets)
of the two factors, is equal to the digits in the product.
.3 (0) x 4 (1) = 1.2 (1). 400 (3) x 3000 (4) = 1,200,000 (7).
.03 (-1) x .004 (-2) = .00012 (-3).
Now if you will set the rule for multiplication of 2 by 4, the slide will protrude at the right-hand end of the stock. In this case the sum of the digits of the two factors is 2, whereas there is only one digit in the product.
The rule for a product which emerges from these simple examples, and which is true for all is:
If the rule is set with the slide protruding at the left-hand end of the stock, the number of digits in the answer is the sum of the digits of the factors. If the slide is protruding at the right-hand end, the number of digits in the product is one less than the sum of the digits of the factors.
Example: Multiply 61.3 x .008 x .24 x 9.19 x 18.6
There are four settings of slide necessary, and we shall find that in three the slide protrudes to the left, and in one to the right. We must, therefore, find the sum of the digits of the five factors and subtract 1, shown in the square bracket, i.e. 2 - 2 + 0 + 1 + 2 - [1] = 2. The final reading in scale D is 201, the result is 20.1.
Problem 14. Multiply .068 x 1200 x 1.68 x .00046 x 28.3
Rule for Division
If you have understood the rule for multiplication you will have no difficulty with the corresponding rule for division, which may now be stated:
If, when dividing, the slide protrudes at the left-hand end of the stock, the number of digits in the result is found by subtracting the number of digits in the divisor from the number in the dividend. If the slide protrudes to the right, the number of digits in the result will be one greater than the difference between the numbers of digits in the dividend and divisor respectively.
Example: 6. 1 / (128 x .039 x 18)
| Set | Slide to: | Digit adjustment |
| 128C to 61D | right | + 1 |
| X to 1C | ||
| 39C to X | right |
-1 |
| X to 1C | ||
| 18C to X | left |
0 |
Result 679 in D under 10C.
Since the slide protruded twice at the right-hand end we must add 2, to the number of digits derived from the factors.
Digits in answer = 1 - 3 - (-1)- 2 + [2]
= 1 - 3 + 1 - 2 + 2 = 1 1.
Result is .0679.
Problem 15. Evaluate 864 / (17 x .0028 x 46.1 x 8.9)
Example: Let us now examine an example such as the following, which consists of simple numbers:
2x 3 x 4 / (1.5 x 8)
We can see at a glance that the answer is 2, since the 1.5 x 8 in the denominator cancels with the 3 x 4 in the numerator, leaving only the 2 as the result.
If you will use your slide rule to find this result, you will see that commencing with the 2 you can divide by 15 and multiply by 3 with one setting of the slide, and then divide by 8 and multiply by 4 with another setting of the slide. When it is possible to carry out two operations at one slide setting you may disregard the position of the slide, i.e. whether to right hand or left hand of the stock, since if digits have to be added or subtracted they will be equal and of opposite signs, and will consequently cancel out. It is only when the slide protrudes to the right and either multiplication or division is effected separately that the number of digits in the result is affected.
We will write down the operations involved in this simple exercise:
| Set | Slide to: | Digit adjustment |
| 15C to 2D | right | + 1 |
| X to 3C | right |
-1 |
| 8C to X | left |
0 |
| Result 2 in D under 4C | left |
0 |
The first and second operations are performed at one setting of the slide. They represent division by 15 followed by multiplication by 3. The slide protrudes to the right hand of the stock, and if we consider these two operations as quite distinct from one another, the digit adjustment will be + 1 for the division and - 1 for the multiplication. These cancel one another. In the third and fourth operation since the slide protrudes to the left-hand end, the digit adjustment is 0 in either case. You will see, therefore, that in cases of combined multiplication and division, you can reduce the check, on the digits to be added or deducted, if you select the factors so that two operations may be performed with the single setting of the slide as often as possible.
Example: Find the value of the following expression:
8.1 x 143 x .0366 x 92.8 x 238 / (62 x 188 x .450 x 85.5)
We will first multiply the five factors in the numerator and follow with the divisions by the four factors in the denominator.
| Set | Slide to: | Digit adjustment |
| l0C to 81D | left | 0 |
| X to 143C | ||
| 1C to X | right | -1 |
| X to 366C | ||
| 10C to X | left | 0 |
| X to 928C | ||
| 1C to X | right | -1 |
| X to 238 | ||
| 62C to X | right | +1 |
| X to 1C | ||
| 188C to X | left | 0 |
| X to 10C | ||
| 45C to X | right | +1 |
| X to 1C | ||
| 85.5C to X | left | 0 |
| Result 209 in D under l0C. | Total | 0 |
| Digits in numerator | = 1 + 3 - 1 + 2+3 | = 8 |
| Digits in denominator | = 2 + 3 + 0 + 2 | = 7 |
| Diff. | 1 |
Collecting the digits gives a total of 1 from the two sources, therefore, the answer is 2.09.
Let us re-work this example by dividing and multiplying alternately to see if the digits rule gives the same result.
| Set | Slide to: | Digit adjustment |
| To 81D set 62C | right | 0 |
| X to 143C | ||
| 188C to X | left | 0 |
| X to 366C | ||
| 45X to X | left | 0 |
| X to 928C | ||
| 85.5C to X | left | |
| Result 209D under 238C | left | 0 |
Take note of the great saving in manipulation of the rule, as compared with doing all the multiplication first and the division afterwards. The digit adjustment is 0 and the result is still the same, 2.09. The operations bracketed together in pairs are those which are effected at one setting of the slide. The first operation of each pair is always a division effected by setting the slide, and the second a multiplication, made by moving the cursor.
As an exercise we suggest you work through the problem for a third time by dividing and multiplying alternately, but taking the factors in a different order from that we have adopted above. The result is quite independent of the order selected, and the digit rule will give the same position for the decimal point.
We leave the decision to you whether you will use these rules for fixing the position of the decimal point or to adopt the approximation method. Apart from slide rule considerations, you will find that to develop the faculty for making quick approximate estimations is useful in many other ways. In a long computation there is a risk that we may overlook a factor and omit it from our slide rule calculation. The chance of doing this is perhaps not great, but if we have several factors in both numerator and denominator we try to select them in pairs, one in the denominator and one in the numerator so that we can use them together in one setting of the slide, and further, we try to select a pair of factors which are near to one another in values, so that the movement of the cursor is small. Now, in making selection of factors to best suit the manipulation of the slide rule lies the risk of omitting a factor. If we subsequently make an approximation to fix the position of decimal point, the omission of a factor may be disclosed.
Additional Examples
We mentioned earlier that we regard the C and D scales as most important in the early
stages of our acquaintance with the slide rule. We therefore now give some additional
examples, graded in difficulty, illustrating the use of these scales. The solutions are
given in each case, but we recommend the reader to work these examples independently and
to refer to the solutions only when in doubt. He will understand that there are
alternative ways of selecting the various factors involved
and he should repeat some of the examples by using different sequences of operations.
Example: A train journey of 437 miles occupies 81hours. What is the average speed?
to 437D set 825C
Under l0C read 53 (53 m.p.h.).
Example: A student obtained 47½ marks out of a possible 78. What is the percentage
marks obtained?
to 475D set 78C
Read 609D under l0C (60.9%).
Example: A group of students obtained the following numbers of marks, in all cases out of a possible 78. Calculate the percentages. 47½, 63, 51½, 72, 65, 23, 37½.
Set 78C to l0D
Read 609D under 475C (60.9%).
,, 808D ,, 63C (80.8%).
,, 66D ,, 515C (66%).
,, 923D ,, 72C (92.3%).
,, 833D ,, 65C (83.3%).
,, 295D ,, 23C (29.5%).
,, 482D ,, 375C (48.2%).
The reader will note that if only one percentage is required, it is best to divide the marks obtained by the marks possible. If a series of results is to be dealt with, it is much quicker to proceed as indicated in this example.
Example: Calculate the weight of water which can be carried in tank 10½ feet long by 3½ feet diameter (1 cu. ft. of water weighs 62.3 lb.).
This computation is:
(p/4) ( 3½)2 x 10.5 x 62.3 lb.
to 35D set 4C
X to 35C
1C to X
X to pC
l0C to X
X to 105C
1C to X
Read 63D under 623C (6300 lb.). Approximation: 3½ squared is about 12, dividing by 4 gives 3 and 3 x p is nearly 10. We have then 10 x 10 = 100 times 62 is 6200. In this example you may shorten the work by squaring 3½ mentally. (7/2)2 = 49 / 4 and combining the 4 under the p we start with p x (49/ 16) x l0.5 x 62.3. This idea of reducing the factors is valuable provided the mental operations are simple. It is a habit all slide rule users soon acquire.
Example: A job takes 8½ days to complete by 19 men working 12½ hours per day. How long would the same job take if the number of men is increased to 23 and the working day reduced to 8 hours?
Result is obtained from 8½ x (19 / 23) x (12½ / 8)
to 85D set 23C
X to 19C
8C to X
Read 10.9D under 125C (11 days).
Example: Compute (4.2 x 71 x 6.76 x .382) / (7.24 x 2.5 x .855)
This example is typical of a large range of problems which give rise to a string of figures which has to be reduced to a numerical answer. The reader will notice no useful cancellation can be made nor is it possible to combine any of the factors mentally. The result can quickly be obtained by combined multiplication and division. A check on the result should be obtained by repeating the slide rule manipulation with alternative factor sequences. In the solution below the factors have been selected in such a manner that the movements of cursor have been reduced to a minimum. This is a desirable practice and should be cultivated by the student.
to 42D set 724C
X to 71C
25C to X
X to 382C
855C to X
Read 498D under 676C.
Result is 49.8, the decimal point being fixed by approximate cancellation.
© Hodder Stoughton, reproduced with permission.