| Slide rules HOME page | INSTRUCTIONS | CONTENTS |
SECTION THREE
THE MODERN SLIDE RULE
Protection of the Slide Rule - Component parts - Sizes of slide rules - C & D Scales - A & B Scales - Log-log Scales - Log Scale - The Cursor - Linear Scales.
THE simple slide rule, consisting of two logarithmic scales drawn on strips of cardboard mentioned in Section 1 would, in actual practice, be inconvenient to use. Clearly the two scales should be linked together by some means, so that whilst they could be made to slide to and fro along one another, they would, when set, retain their positions and not fall apart. In order to mark any point in a scale when desired, a movable index would be a useful adjunct to the scales. We shall find that these points have not been overlooked in the slide rule as we find it to-day.
We do not propose to write a long description of the modern slide rule. We assume that the reader possesses a slide rule, or, at least, has access to one, and the mechanical construction of the instrument is so straightforward that we would not presume to enter into superfluous details.
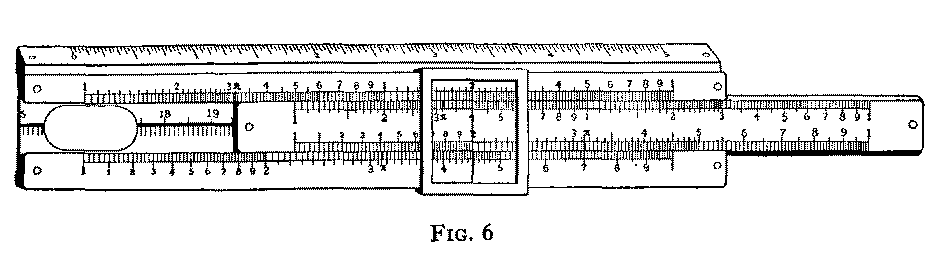
There are a few points which we believe may be mentioned with advantage, and we think illustrations of a de-luxe instrument, and also an inexpensive type, should be included in this section. These are shown in Figs. 6 and 7 respectively.

Whatever type of slide rule you decide to buy we ask you to take great care of it. The manufacture of slide rules is a technical and highly skilled craft, and much painstaking effort goes into their production. Your slide rule should be protected from exposure to heat and damp. You should particularly avoid leaving it lying exposed to the direct rays of the sun in warm weather. The majority of slide rules are constructed in part of celluloid; this material discolours and shrinks if unduly exposed. When not in use please replace the rule in the protective case supplied with it, and put away in a cool, dry place, preferably in the drawer of your desk.
Since we frequently refer to them, we think we should mention the names of the component parts of a slide rule. The body of the rule is usually termed the"stock". The smaller part which can be moved to right or left, is called the "slide", and the movable index is known as the cursor.
If you will examine the stock you will find it is built up of several parts which give it a degree of flexibility. If the stock was just a solid strip of wood with the necessary grooves machined in it to accommodate the slide and the cursor, it would invariably in the course of time warp sufficiently to grip the slide tightly and make the manipulation of the rule difficult or impossible. We have seen such rules with the slides so tight that it has been necessary to use a hammer or something similar to drive the slides out.
The 10" rule is the popular size. In this the scales are 10", or sometimes 25 cm., in length, and the overall length of the rule 11" or 12". More convenient to carry in the pocket is the 5" rule. There are also available rules of lengths 15" or 20" or more.
Cylindrical and circular instruments are made which employ the logarithmic principles and these are commonly called slide rules, although the term is certainly not appropriate. We shall make a brief mention of these instruments at a later stage.
You will notice that there are several scales on the rule. The layout of scales is varied to adapt the rule to different requirements. If your rule is one of the general-purpose type it will be equipped, among others, with two scales usually denoted by the letters C and D. Scale C lies along the bottom edge of the slide, and scale D is on the stock adjacent to scale C. These two scales are identical in their graduations and are, in reality, one single scale which has been cut through lengthwise. The main graduations of scales C and D are numbered 1, 2, 3, etc., up to 10. Subdivisions should be numbered as fully as possible without carrying the process to the extent of causing confusion. The scales of some slide rules are numbered in a very confusing manner. We contend that when subdivisions are numbered the figure marked on them should be exact and not abbreviated. In some of the higher-priced rules the principal subdivisions between main divisions 1 and 2 of scales C and D are marked 1, 2, 3, etc., up to 9. These figures should be 1.1, 1.2, 1.3, etc., up to 1.9, We recommend the reader to avoid purchasing a rule in which the scale numbering is abbreviated, as it will inevitably involve him in errors due to misreading the scales.
Scales C and D are those most frequently used of all; we have mentioned them first and shall return to them in Section 4.
Scales A and B lie adjacent to one another, A on the stock and B along the upper edge of the slide. The numbering of the main divisions of scales A and B, starting from the left-hand end, should be 1, 2, 3, etc., up to 10, then 20, 30, etc., up to 100. The figure 10 marks the line mid-way along the length of the scale. The principal sub-divisions should also be numbered as far as conveniently possible. Abbreviated figures should be avoided for the reason mentioned earlier.
At this stage we would ask you in all seriousness not to acquire the very bad habit of using Scales A and B for multiplication and division, The objection to this practice lies in the fact that when the A and B scales of a 10" rule are so used, the instrument, in effect, becomes a 5" rule, and results cannot be obtained with the same degree of accuracy as when the C and D scales are used. It is true that when scales A and B are employed, the results need never be "off the scale", but accuracy should not be sacrificed for a doubtful gain in convenience.
Until comparatively recently scales A, B, C and D were often all that appeared on the face of the rule. As a result of the change in manufacturing technique referred to earlier, it became possible to include other scales without increasing production costs to any great extent. "Unique" slide rules, almost since their inception, have carried log-log scales in many models, and these scales are now taken for granted. Their inclusion certainly adds value to a slide rule, They are not difficult to understand as will be shown presently.
In the absence of log-log scales the combination of the A, B, C and D scales is probably the best that could be devised, but if a slide rule is equipped with log-log scales we think the provision of the A and B scales is unnecessary, and that other scales can be substituted for them which increase the usefulness of the rule. Section 10 deals with rules designed on these lines.
Scales A and B in conjunction with scales C and D give a quick means of extracting square and cube roots, and of squaring and cubing numbers. Since scale D is twice the length of each of the identical halves of scale A, it follows that in moving along scale A, you will be passing the logarithmic "milestones", twice as fast as when moving along scale D. Now, if you double the logarithm of a number, you will arrive at the logarithm of the square of that number. Please examine your rule and with the aid of a cursor project readings in scale D to scale A - or from scale C to scale B on the slide. You will see that opposite 2 in D appears 4 in A, and for every number in D the square of that number appears in A.
Square roots are very quickly obtained by reversing the process and projecting from
scale A into scale D. The problems of cubing numbers and extracting cube roots are in like
manner facilitated by using the four scales A, B, C and D, and we shall return to this
problem at a later stage. If log-log scales are included in your slide rule, all powers
and roots of numbers may be evaluated easily, and it is for this reason we say that the A
and B scales are of doubtful value, since their uses in the processes of evolution and
involution are very limited. Log-log scales give the means in conjunction with scale D of
evaluating any power or any root
of any number, whereas scales A and B will only deal with powers and roots of 2 or 3, and
multiples of 2 or 3.
We have mentioned log-log scales several times. When included in a slide rule these scales are often placed along the top and bottom edges of the stock. Please refer to Fig. 7 and you will see the log-log scales; they are marked LU and LL, at the left-hand end of the rule.
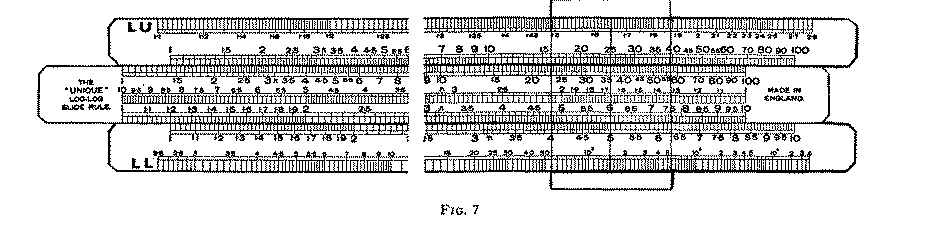
Log-log scales are very useful in dealing with certain technical problems. We have heard the opinion expressed that log-log scales give the appearance of complexity to the face of the slide rule, and, since they are seldom used, they should not be included. We do not agree. The log-log scales are not obtrusive, and one quickly learns to ignore them when not required, and we have not found them inconvenient or confusing. They are sometimes to be found on the reverse of the slide as mentioned later on.
Section 6 deals with the problems which demand the provision of log-log scales and which cannot be solved by the slide rule without the aid of them.
The primary object of this book is to attempt to remove the impression that the slide rule is a difficult instrument to use. If, therefore, any reader feels that he prefers the very simplest slide rule with only the A, B, C and D scales included, we agree that he may be well advised to use this type, especially if his work is of a straightforward nature, and not likely to involve the use of log-log or trigonometrical scales.
If you will look at the under surface of the slide of your rule you will probably see two or perhaps three scales.
The scale marked S is a scale of sines. Its graduation will probably commence at a value of 35 minutes - marked 35' - and finish at 900. This scale is used in conjunction with scale A.
The tangent scale will be labelled T. Graduations may start just below 6° and proceed to 45°, Alternatively, the tan scale may start at 34' and finish at 45° In the former case the T scale is used in conjunction with the D scale; in the latter case it is used with the A scale.
In some rules the S and T scales appear on the face of the rule. Some people prefer this arrangement of scales, and the manufacture of the rule is simplified when it is adopted. The disadvantage lies in the fact that the face of the rule becomes somewhat congested with these additional scales.
If you will look carefully at the S and T scales you may see that unlike the A, B, C
and D, and log-log scales, they are not subdivided consistently in tenths, fifths, etc.
Below 20° on the S scale, and throughout the T scale, the unit divisions are subdivided
into sixths, twelfths, etc. This system of subdivision is adopted because we do not always
work in decimals of a degree, but we use the corresponding number of minutes, and as you
will see subdivision into sixths, etc., is more convenient
for this purpose, there being 60 minutes in one degree.
In recent years manufacturers have adopted the practice of subdividing in decimals to the S and T scales. The reader may encounter slide rules in which the minutes' graduations have given place to decimals of degrees.
Section 7 deals with examples of trigonometrical work employing scales S or T.
The third scale on the reverse side of the slide is an evenly divided scale, usually marked L, which enables us in conjunction with scale D to read off logarithms of numbers. If the scales on your rule are 10" long, you will see that the log scale is subdivided into tenths and fiftieths, and it is, in effect, a 10" measuring rule. As a matter of fact, you can obtain logarithms of numbers with the aid of an ordinary rule used in conjunction with scale C or D.
The scales mentioned in this section are, with the exception of the log-log scales, those you will find in the ordinary or standard type of slide rule; the type which seems to be preferred by the large majority of users. In later sections we shall deal with slide rules provided with different arrangements of scales.
In closing this section we would add a note of warning concerning the cursor. We strongly recommend the reader to purchase a slide rule which is fitted with a ''free-view" cursor. The best type of cursor is that which has supports on only its top and bottom edges for engaging with the grooves in the stock. Some types have a light rectangle frame into which the glass or celluloid window is fitted. The edges of the frame lie across the face of the rule and obliterate to some extent the figures and graduations of the scales, and create an element of uncertainty and add to the possibility of making errors. One form of cursor, now only occasionally seen, has fitted on one side of it a small index and scale, designed to assist in fixing the position of the decimal point in the numerical result. This form of cursor hides a considerable part of the scales, and generally is a source of annoyance.
On some cursors you may find two or three hair lines. The additional lines give assistance in calculations concerning areas of circles, etc. Confusion may arise when multiple-line cursors are used, and we prefer the simple free-view cursor with a single hair line.
We would say a word concerning the linear scales which are often fitted to slide rules. These have no connection with the rule as a calculating device. They add to the appearance of a rule, but we think they are entirely superfluous. A slide rule should be always handled carefully, and it is one of the minor annoyances in life to see it used for ruling lines or to take measurements when a wooden office ruler or a steel rule should be used.
© Hodder Stoughton, reproduced with permission.