SECTION ONE

THE PRINCIPLE OF THE SLIDE RULE

Linear and non-linear scales - numbering of the scales - reading the scales - multiplication and division of simple numbers.

The reader will agree that the arithmetical operations of addition and subtraction are less tedious to carry out than those of multiplication and division. When very simple numbers are involved, none of these four operations gives trouble, and it is just as simple to multiply 4 by 2 as to add together 4 and 2. When the numbers are larger, this is no longer the case. It is still comparatively easy to add together, say 492 and 374; most people could perform the operation mentally, and give the result as 866, without resorting to the aid of pencil and paper. If, however, these two numbers have to be multiplied together, only a few people who have the unusual gift of being able to cope with such computations mentally could give the answer with confidence. As a test of memory and concentration write down these numbers with a view to multiplication, namely, 374 x 492 ; now lay down your pencil and try to complete the multiplication, memorising the figures as they emerge, and then mentally add up the three resulting lines. It is clear that to obtain a correct result one must possess exceptional powers; in fact, to perform mentally the operations correctly with two figure factors is commendable. Addition or subtraction remain comparatively simple, and can be quickly performed with even a dozen or any number of factors, but multiplication and division when carried out by ordinary arithmetical means become progressively tedious as the number of factors increases.

Linear and non-linear scales

There are now in use, for office and industrial purposes, ingenious calculating machines. These are, comparatively, of recent origin, and are designed rapidly to deal with the masses of routine computations which have to be dealt with in large offices, banks and industrial organisations. For their particular purposes they stand supreme, and it is no part of this treatise to deal with them. To some extent these elaborate and expensive machines execute the same operations as the simple slide rule, but many operations which can be effected by slide rule are impossible with the calculating machine, and the converse applies also.

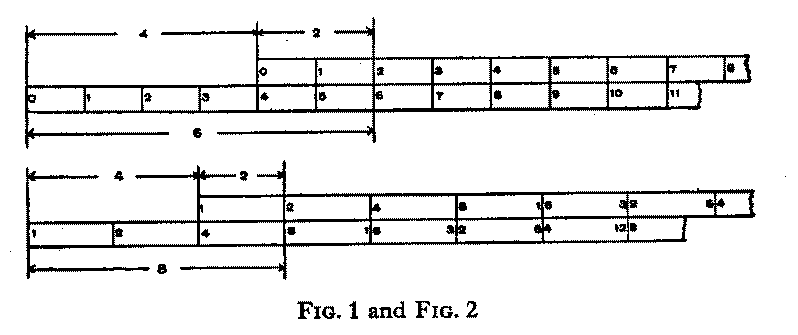
Reverting to our simple addition of 4 and 2, it is clear that we could perform the operation with the use of two scales placed as shown in Fig. 1. These scales might be divided in inches or in centimetres, or in any arbitrary unit, and if each unit was subdivided into tenths we could effect the addition of such quantities as 3.6 + 7.8 Further, if we had a convenient way of marking the result of the first addition by means of an index sliding along the lower scale, we could proceed to add or subtract as many factors as we desired. The reader will have no difficulty in seeing how subtraction would be effected, and he need not be much concerned at the possibility of requiring an absurdly long lower scale, since we are not suggesting that anyone would indulge in this unpracticable demonstration, we are leading up to the slide rule method of multiplication. We have, however, occasionally seen a mechanic adopt this method of adding together dimensions shown in a drawing of some engineering product. He may wish to add 6 11/16" to 2 1/8" and subtract 1 3/32". The fractions give him a little trouble, so he takes his steel rule and places his thumb nail against the line marking 6 11/16". With a finger of his other hand he counts off a further 2 1/8" and moves his thumb to register the new position further along the rule, and finally counts back 1 3/32". The last mark gives him the result he is seeking.

Numbering of the scales

Now please examine the scales indicated in Fig. 2. You will first notice that while the end divisions are marked 0 in Fig. 1 they are marked 1 in Fig. 2. You will also observe that whereas in Fig. 1 the graduations are marked 0, 1, 2, 3, etc., in Fig. 2 they are marked 1, 2, 4, 8, 16, etc., each number being twice the value of the preceding one. Clearly, if all the graduations were shown in Fig. 2, there would be a great crowding together as we move in the right-hand direction along the scale.
For instance, the distance lying between graduations 1 and 2 is about 1/2". In this same space between graduations 16 and 32, it would be necessary to crowd in 16 smaller spaces.

The scales of Fig. 2 are logarithmic, and you will understand their properties when you have perused the section on logarithms. (There is no necessity to break off at this stage to read about logarithms, and we recommend that you read on without concern for them.) Fig. 1 gave us the sum of 4 and 2. Fig. 2 gives us the product of 4 and 2, i.e. 8, and it becomes evident that one of the rules of logarithms is that by adding them together we are effecting multiplication of numbers, and when we subtract one from another we are dividing.

In these simple facts lies the principle of our slide rule, which, in effect, is the equivalent of a table of logarithms arranged in a convenient form for rapid working.

Further study of Fig. 2 will show that the scales are set so that we can at once read off 4 x 2= 8; 4 x 4= 16; 4 x 8= 32, and if the scale had been extended and subdivided we should have been able to read off many other results.

The procedure for multiplication of two factors is:

(a) Select any one of the factors and note its position in the lower scale.
(b) Slide the upper scale to the right, to bring the 1 of this scale opposite the factor noted in the lower scale.
(c) Find the second factor in the upper scale.
(d) Directly below the second factor, read the number which you will see in the lower scale. This number is the answer to the multiplication of these two factors.

We know that these instructions sound rather forbidding, but they are quite simple and if the reader will follow them through carefully he will, in the course of a few minutes, learn to use the two scales for multiplication. It will certainly assist if the scales are drawn out on two strips of cardboard, so that they can be moved along one another into the different positions.

Division is effected by using the scales to subtract the logarithm of the divisor from the logarithm of the dividend. Referring once more to Fig. 2, we see at once that in order to divide, say, 128 by 32, we slide the upper scale along until the 32 in it .stands immediately above the 128 in the lower scale. Then opposite the 1 of the upper scale we read the answer, 4, in the lower scale. Fig. 3 shows you a logarithmic scale which has been subdivided between the primary numbers. You will notice that between graduations 1 and 2 it has been possible to show twenty smaller spaces, whereas between 9 and 10 only 5 subdivisions have been made. This change in the distance between consecutive lines is a feature of all logarithmic scales; it is the crowding together we have mentioned earlier.

Reading the scales

We now come to what may prove a difficulty for some readers to whom scales are not familiar. We refer to what is generally termed "reading the scales". We will, therefore, spend a little time in studying this difficulty since it is quite certain that ability to read the scales easily and with certainty is essential. The difficulty - if there is any - lies in the fact that the graduations of the scale alter. In Fig. 3, the distance between 1 and 2 is subdivided into 20 parts. If the subdivision continued in the same way, the spaces would soon become inconveniently small. At the division 2 a change in the dividing occurs, and the space between 2 and 3 is subdivided into only 10 parts, and this subdividing continues from 3 to 4 and again from 4 to 5. At 5 another change becomes necessary and the main divisions from 5 to 10 are now subdivided each into five parts only.

In reading any position of the scale, the graduations on either side of that position must be examined. Look along the scale to the nearest main figure, then note whether the subdivisions are tenths or fifths or any other fractions of the main division. With a very little practice you will quickly develop the faculty of reading the positions in the scale with a high degree of accuracy.

As examples let us attempt to read the positions in the scale of the four lines marked a, b, c and d of Fig. 3. Line a exactly coincides with a division of the scale and appears to be about midway between 1.4 and 1.5 The position of the line a, therefore, is 1.45. Line b also coincides with a division of the scale and lies between main numbers 2 and 3. A glance shows that there are ten sub-divisions between 2 and 3. The graduation immediately to the right of 2 is 2.1, and the next to the right is 2.2, and it is at this position that line b stands. Line c lies between numbers 5 and 6, and now we find there are only 5 subdivisions in this space. We will write down fully the readings of the lines at this part of the scale; they are 5.0, 5.2, 5.4, 5.6 5.8 and 6.0 Line c clearly stands at 5.6. Line d does not coincide with any graduation in the scale and now our ability to estimate fractions must be exercised. Line d lies between 7.4 and 7.6 Let us try to visualise the small distance between these two lines being further subdivided into five smaller spaces. There would now be four lines very close to one another in between the lines at 7.4 and 7.6, and the readings of these four lines would be 7.44, 7.48, 7.52 7.56 and we estimate that line d is very near to 7.48.

The observant reader may object with some justification that there is a fundamental error involved in the method we have adopted in arriving at the value 7.48. He will have noticed that in effect we have estimated the position of the line d as being the of the distance between 7.4 and 7.6 and he will point out that even if our estimate is quite correct the true position of the imaginary line 7.48 is not exactly at this point, because the scale being logarithmic the five small spaces between 7.4 and 7.6 are not equal to one another. Actually the imaginary 7.48 line is slightly to the right of the position we have assigned to it. This is typical of the errors we invariably make when we estimate the positions of points which do not coincide with any real lines in the scale. We shall return to this matter when we consider later on the degree of accuracy possible when using a slide rule, but the inquisitive reader may care to know that the true scale reading of a point exactly 2/5ths of the distance along 7.4 - 7.6 of the scale is 7.476. Our estimate has involved us in the small error of 4 parts in 7000. To obtain an idea of what this error means, imagine you are asked to measure the length of the table at which you are working. By means of a rule or tape and measuring carefully you find the length is, say, 56.4 inches, whereas when measured with more precise apparatus the length is found to be 56.43 inches; the error you have made is, therefore, three hundredths of an inch, and proportionately these two errors are nearly equal.

Multiplication and division of simple numbers

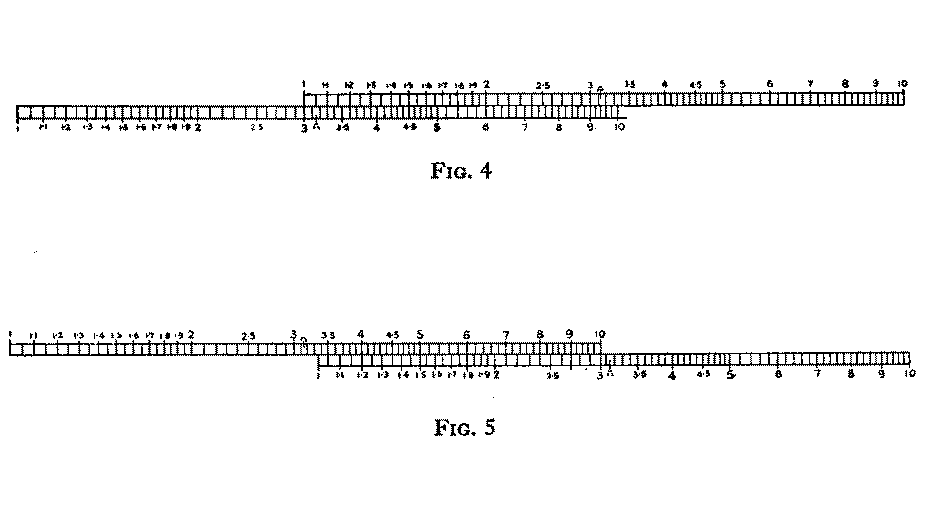
Fig. 4 illustrates two scales set so that we can multiply 3 by various numbers. Notice that directly under any number in the upper scale, three times that number appears in the lower scale, e.g. 3 x 11 = 33, 3 x 12 = 36, 3 x 2 = 6 and several others. This same setting of the scales shows how we can divide 9 by 3, or 6 by 2, etc. Now, in Fig. 4 the upper scale projects to the right beyond the lower, and we cannot read results directly under the projecting part. This difficulty is surmounted by sliding the upper scale to the left a distance equal to its own length. Fig. 5 shows these new positions of the scales and now we can perform multiplications such as 4 x 3 = 12, 6 x 3 = 18, 9 x 3 = 27, and we can also divide 18 by 6 or 15 by 5, etc.

We do not wish to weary the reader by pursuing unduly this very elementary conception of the slide rule. This book is primarily designed to assist readers who have had no previous acquaintance with the slide rule, and we think that those who have persevered so far will, by now, realise that there is nothing difficult to learn and that the manipulation of a slide rule is very simple indeed. We feel that we should now pass on to examine the slide rule in its modern practical form. (The next section deals with fractions and decimals. It is included to assist readers who may have difficulty in reading the scales in the decimal system. It should be ignored by others.)

© Hodder Stoughton, reproduced with permission.