Taken from "A Treatise on Mathematical Instruments" by J. F. Heather (1870).
My thanks to Jim Bready who scanned the document on which this is based

THE SECTOR.

This instrument may well be called a universal scale. By its aid all questions in proportion may be solved; lines may be divided either equally or unequally into any number of parts that may be desired; the angular functions, viz., chords, sines, tangents, &c., may be set off or measured to any radius whatever; plans and drawings may be reduced or enlarged in any required proportion; and, in short, every operation in geometrical drawing may be performed by the aid of this instrument and the compasses only.

The name sector is derived from the tenth definition of the third Book of Euclid, in which this name is given to the figure contained by two radii of a circle, and the circumference between them. The instrument consists of two equal rulers, called legs, which represent the two radii, movable about the centre of a joint, which centre represents the centre of the circle. The legs can consequently be opened so as to contain any angle whatever, or completely opened out until their edges come into the same straight line.

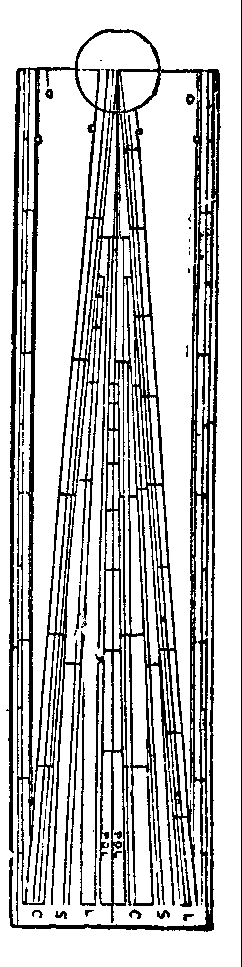Sectors are made of different sizes, and their length is usually denominated from that of the legs when shut together. Thus, a sector of 6 inches, such as is supplied in the common pocket cases of instruments, forms a rule of 12 inches when opened; and this circumstance is taken advantage of, by filling up the spaces not occupied by the sectorial lines with such lines as it is most important to lay down upon a greater length than the 6-inch plain scale will admit. Among these the most usual are (1) the lines of logarithmic numbers, sines, and tangents, described in Part II. ; (2) a scale of 12 inches, in which each inch is divided into ten equal parts; and (3) a foot divided into ten equal primary divisions, each of which is subdivided into ten equal parts, so that the whole is divided into 100 equal parts. The last-mentioned is called the decimal scale, and is placed on the edge of the instrument.

The sectoral lines proceed in pairs from the centre, one line of each pair on either leg, and are, upon one face of the instrument, a pair of scales of equal parts, called the line of lines, and marked L; a pair of lines of chords, marked C; a pair of lines of secants, marked S; a pair of lines of polygons, marked POL. Upon the other face, the sectoral lines are - a pair of lines of sines, marked S; a pair of lines of tangents up to 45°, marked T; and a second line of tangents to a lesser radius, extending from 45° to 75°.

Each pair of sectoral lines, except the line of polygons, should be so adjusted as to make equal angles at the centre, so that the distances from the centre to the corresponding divisions of any pair of lines, and the transverse distance between these divisions, may always form similar triangles. On many instruments, however, the pairs of lines of secants, and of tangents from 45° to 75°, make angles at the centre equal to one another, but unequal to the angle made by all the other pairs of lines.

The solution of questions on the sector is said to be simple when the work is begun and ended upon the same pair of lines; compound, when the operation is begun upon one pair of lines and finished upon another.

In a compound solution the two pairs of lines used must make equal angles at the centre, and, consequently, in the exceptional case mentioned above, the lines of secants and of tangents above 45° cannot be used in connection with the other sectoral lines. (Since, however, secant : rad. : : rad. : cosine : and tangent : rad. : : rad. : cotangent; the line of sines may be used with the other sectoral lines in place of the line of secants, and the line of tangents less than 45°in place of the line of tangents greater than 45°, the complements of the angles being taken upon these lines, in either case, instead of the angles themselves. See later.)

When a measure is taken on any of the sectoral lines beginning at the centre, it is called a lateral distance; but when a measure is taken from any point on one line to its corresponding point on the line of the same denomination on the other leg, it is called a transverse or parallel distance.

The divisions of each sectoral line are contained within three parallel lines, the innermost being the line on which the points of the compasses are to be placed, because this is the only line of the three which goes to the centre, and is therefore the sectoral line.

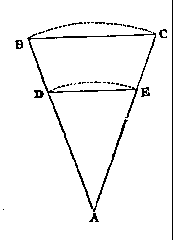
On the principle of the Use of the Sectoral Lines.- lst. In the Case of a Simple Solution.- Let the lines AB, AC represent a pair of sectoral lines, and BC, DE any two transverse distances taken on this pair of lines; then, from the construction of the instrument, we have AB equal to AC, and AD equal to AE, so that AB : AC : : AD:AE, and the triangles ABC and ADE have the angle at A common, and the sides about this common angle proportional; they are, therefore, similar (Euc. vi. prop. 6) and -  AB : BC : : AD : DE.

In the case of a compound solution, the angles at A are equal, but not common, and the reasoning is, in all other respects, exactly the same.

 

USES OF THE LINE OF LINES.

To find a Fourth Proportional to Three given Lines. - Set off from the centre a lateral distance equal to the first term, and open the sector till the transverse distance at the division thus found, expressing the first term, is equal to the second term; again, extend to a point whose lateral distance from the centre is equal to the third term, and the transverse distance at this point will be the fourth term required.

If the legs of the sector will not open far enough to make the lateral distance of the second term a transverse distance at the division expressing the first term, take any aliquot part of the second term which can conveniently be made such transverse distance, and the transverse distance at the third term will be the same aliquot part of the fourth proportional required.

A third proportional to two given lines is found by taking a third line equal to the second, and finding the fourth proportional to the three lines.

Example. - To find a fourth proportional to the numbers 2, 5,and 10. Open the sector till the lateral distance of the second term 5 becomes the transverse distance at 2, the first term; then the transverse distance at 10 will extend, as a lateral distance, from the centre to 25, the fourth proportional required.

To bisect a given Straight Line. - Take the extent of the line in the compasses, and open the sector till this extent is a transverse between 10 and 10 on the line of lines : then the transverse distance from 5 to 5 on the same pair of sectoral lines gives the half of the line, and this extent set off from either end will bisect it.

To divide a Straight Line into any Number of equal Parts. - 1. When the number of parts is a power of 2, the operations are best performed by continual bisection. Thus, let it be required to divide the line AB into sixteen equal parts. (1.) Make AB a transverse distance between 10 and 10 on the line of lines; then take
off the transverse distance of 5 and 5 and set it off from A or (Greater accuracy is obtained by setting off the distance from both ends of the extent to be bisected, and then, in case the two points so found do not accurately coincide, taking the middle point between them, as near as the eye can judge, for the true point of bisection.) B to 8,and AB will be divided into two equal parts at the division 8. (2.) Make A 8 a transverse distance at 10, and then the transverse distance at 5, set off from A or 8 at 4, and from B or 8 at 12, will divide the line into four equal parts at the divisions 4, 8, and 12. (3.) Make the extent A 4 a transverse distance at 10, and the transverse distance at 5 will again bisect each of the parts last set off, and divide the whole line into eight equal parts at the divisions 2, 4, 6, 8, 10, 12, and 14. Each of these may be again bisected by taking the transverse distance at 2½ or 2·5, that is, at the middle division between the 2 and the 3 upon the line of lines, and the line will be divided as required.

When the divisions become smaller than can be conveniently bisected by the method just explained, the operation may still be continued to any required extent by taking the extent of an odd number of the divisions already obtained as the transverse distance of 10 and 10, and setting off the half of this extent, or the transverse distance at 5, from the several divisions already obtained. Thus, in the preceding example, by making the extent of three of the divisions, or five, or seven, a transverse distance at 10, the transverse distance at 5, set off from the several divisions already obtained, will divide AB into 32 equal parts.

2. When the number of parts is not a power of 2, the operations cannot all be performed by bisections; but still, by a judicious selection of the parts into which the line is first divided, many of the after-operations may be performed by bisections. Example. - Let it be required to divide the line AB into seven equal parts. (1.)

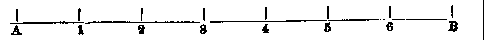
Make the whole extent, AB, a transverse distance between 7 and 7 on the line of lines; then take off the transverse distance of 4 and 4, and set it off from A and B to 4 and 3. (2.) Make this extent from A to 4 a transverse distance at 10; then the transverse distance at % bisects A 4 and 3 D in 2 and 5; set off from 3, gives 1, and from 4 gives 6; and thus the line AB is divided into seven equal parts as required.

To open the Sector so that the Line of Lines may answer for any required Scale of equal Parts. - Take one inch in the compasses, and open the sector till this extent becomes a transverse distance at the division indicating the number of parts in an inch of the required scale; or, if there be not an integral number of parts in one inch, it will be better to take such a number of inches as will contain an integral number of parts, and make the extent of this number of inches, if it be not too great, a transverse distance at the division indicating the number of parts of the required scale in this extent.

Example. - To adjust the Sector as a Scale of One Inch to Four Chains. - Make one inch the transverse distance of 4 and 4; then the transverse distances of the other corresponding divisions and subdivisions will represent the number of chains and links indicated by these divisions : thus, the transverse distance from 3 to 3 will represent three chains; the transverse distance at 4·7, or the seventh principal subdivision after the primary division marked 4, will represent 4 chains 70 links, and so on.

To construct a Scale of Feet and Inches in such a manner that an extent of Three Inches shall represent Twenty Inches. - 1. Make three inches a transverse distance between 10 and 10, and the transverse distance of 8 and 8 will represent 16 inches. 2. Set off this extent from A to B, divide it by continual bisection into 16 equal parts, and place permanent strokes to mark the first 12 of these divisions, which will represent inches. 3. Place the figure 1 at the twelfth stroke, and set off again the extent of the whole 12 parts, from 1 to 2, 2 to 3, &c., to represent the feet.

As an example of the Use of the Line of Lines in reducing Drawings, let it be required to reduce the Linear Dimensions of a Drawing in the Proportion of 8 to 5. - 1. Take in the compasses the distance between two points of the drawing, and make it a transverse distance at 8 and 8; then the transverse distance of 5 and 5 will be the distance between the two corresponding points of the copy. 2. These two points having been laid down, make the distance between one of them and a third point a transverse distance at 8, and with the transverse distance at 5 describe, from that point as centre, a small arc.

3. Repeat the operation with the other point, and the inter section of the two small arcs will. give the required position of the third point in the copy. In the same manner all the other points of the reduced copy may be set off, each one from two points previously laid down.

LINE OF CHORDS.

The double scales of chords upon the sector are more generally useful than the single line of chords laid down on the plain scale; for, on the sector, the radius with which the arc is to be described may be of any length between the transverse distance of 60 and 60 when the legs are closed, and that of the transverse of 60 and 60 when the legs are opened as far as the instrument will admit of; but, with the chords on the plain scale, the arc described must be always of the same radius.

To protract or lay down a right-lined Angle DAC, which shall contain a given Number of Degrees, suppose 46°. -  Case 1.When the angle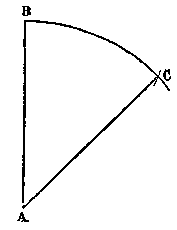
contains less than 60°, make the transverse distance of 60 and 60 equal to the length of the radius of the circle, and with that opening describe the arc BC. Take the transverse distance of the given degrees 46, and lay this distance on the arc from the point B to C. From the centre A of the arc draw two lines AC, AB, each passing through one extremity of the distance DC laid on the arc, and these two lines will contain the angle required. Case 2. When the angle contains more than 60° Suppose for example, we wish to form an angle containing 138°. Describe the arc DCB, and make the transverse distance of 60 and 60 equal the radius as before. Take the transverse distance of ½ or ¹/₃   &c., of the given number of degrees, and lay this distance on the arc twice or thrice, as from B to a, a to b, and from b to D. Draw two lines connecting B to A, and A to D, and they will form the angle required.

When the required angle contains less than 5°, suppose 3½, it will be better to proceed thus. With the given radius, and from the centre A, describe the arc DG; and from some point, D, lay off the chord of 60°, which suppose to give the point G, and also from the same point D lay off in the same direction the chord of 56½° (== 60°  -  3½°), which would give the point E. Then through these two points E and G, draw lines to the point A, and they will represent the angle of 3½° as required.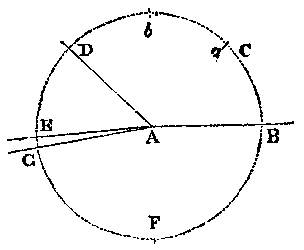

From what has been said about the protracting of an angle to contain a given number of degrees, it will easily be seen how to find the degrees (or measure) of an angle already laid down.

LINE OF POLYGONS.

The line of polygons is chiefly useful for the ready division of the circumference of a circle into any number of equal parts from 4 to 12; that is, as a ready means to inscribe regular polygons of any given number of sides, from 4 to 12, within a given circle; to do which, set off the radius of the given circle (which is always equal to the side of an inscribed hexagon) as the transverse distance of 6 and 6 upon the line of polygons. Then the transverse distance of 4 and 4 will be the side of a square; the transverse distance between 5 and 5, the side of a pentagon; between 7 and 7, the side of a heptagon; between 8 and 8, the side of an octagon; between 9 and 9, the side of a nonagon, &c., all of which is too plain to require an example.

If it be required to form a polygon, upon a given right line, set off the extent of the given line, as a transverse distance, between the points upon the line of polygons answering to the number of sides of which the polygon is to consist; as for a pentagon between 5 and 5; or for an octagon between 8 and 8: then the transverse distance between 6 and 6 will be the radius of a circle whose circumference would be divided by the given line into the number of sides required.

The line of polygons may likewise be used in describing, upon a given line, an isosceles triangle, whose angles at the base are each double that at the vertex. For, taking the given line between the compasses, open the sector till that extent becomes the transverse distance of 10 and 10, then the transverse distance of 6 and 6 will be the length of each of the two equal sides of the isosceles triangle.

All regular polygons whose number of sides will exactly divide 360 (the number of degrees into which all circles are supposed to be divided) without a remainder may likewise be set off upon the circumference of a circle by the line of chords. Thus, take the radius of the circle between the compasses, and open the sector till that extent becomes the transverse distance between 60 and 60 upon the line of chords; then, having divided 360 by the required number of sides, the transverse distance between the numbers of the quotient will be the side of the polygon required. Thus, for an octagon, take the distance between 45 and 45; and for a polygon of 36 sides take the distance between 10 and 10, &c.

LINES OF SINES, TANGENTS, AND SECANTS.

Given the Radius of a Circle (suppose equal to two inches), required the Sine and Tangent of 28° 30' to that Radius. - Open the sector so that the transverse distance of 90 and 90 on the sines, or of 45 and 45 on the tangents, may be equal to the given radius, viz., two inches; then will the transverse distance of 28° 30', taken from the sines, be the length of that sine to the given radius, or, if taken from the tangents, will be the length of that tangent to the given radius.

But if the Secant of 28° 30' is required, make the given radius of two inches a transverse distance of 0 and 0 at the beginning of the line of secants, and then take the transverse distance of the degrees wanted, viz., 28° 30'.

A Tangent greater than 45° (suppose 60°) is thus found: -  Make the given radius, suppose two inches, a transverse distance to 45 and 45 at the beginning of the line of upper tangents, and then the required degrees (60) may be taken from the scale.

The tangent to a given radius of any number of degrees greater than 45° can also be taken from the line of lower tangents, if the radius can be made a transverse distance t the complement of those degrees on this line (see note above).

Example. - To find the tangent of 78° to a radius of two inches. Make two inches a transverse distance at 12 on the lower tangents, then the transverse distance of 45 will be the tangent of 78°.

In like manner the secant of any number of degrees may be taken from the sines, if the radius of the circle can be made a transverse distance to the complement of those degree upon this line. Thus, making two inches a transverse distance to the sine of 12°, the transverse distance of 90 and 90 will be the secant of 78°.

To find, by means of the lower tangents and sines, the degrees answering to a given line, greater than a given radius which expresses the length of a tangent or secant to this radius. For a tangent, make the given line a transverse distance at 45 on the lower tangents; then take the extent of the given radius, and apply it to the lower tangents; and the complement of the degrees at which it becomes a transverse distance will be the number of degrees required. For secant make the given line a transverse distance at 90 on the sines; then the extent of the radius will be a transverse distance at the complement of the number of degrees required

Given the Length of the Sine, Tangent, or Secant of an Degrees, to find the Length of the Radius to that Sine, Tangent or Secant . - Make the given length a transverse distance to it given degrees on its respective scale. Then,

To find the Length of a versed Sine to a given Number of Degrees and a given Radius. - 1. Make the transverse distance of 90 and 90 on the sines equal to the given radius. 2 Take the transverse distance of the sine of the complement of the given number of degrees. 3. If the given number of degrees be less than 90, subtract the distance just taken, viz. the sine of the complement, from the radius, and the remainder will be the versed sine : but, if the given number of degrees is more than 90, add the complement of the sine to the radius, and the sum will be the versed sine.

To open the legs of a Sector, so that the corresponding double Scales of Lines, Chords, Sines, and Tangents may make each a Right Angle. -  On the line of lines make the lateral distance 10, a transverse distance between 8 on one leg and 6 on the other leg.

On the line of sines make the lateral distance 90, a transverse distance from 45 to 45; or from 40 to 50; or from 30 to 60; or from any degree to its complement.

On the line of sines make the lateral distance of 45 a transverse distance between 30 and 30.

Return to Sector in collection