| Slide rules HOME page | INSTRUCTIONS | MANUALS | < SITE MAP > |
REVISED INSTRUCTIONS
FOR THE USE OF
A. W. FABER'S CALCULATING RULE
Note: Some of the images are large (c 150kb) but each includes about 5 figures. This was necessary to provide the detail. If you wish to work with this document it might be preferable to download and print the figures.]
CONTENTS
Introduction
Construction of
the Calculating Rule
The Scales
Proportion
Multiplication
Division
Combined Multiplication
and Division
The Inverted Slide
Squares and Square Roots
Cubes and Cube Roots
Fourth Powers and Roots
PRACTICAL ILLUSTRATIONS OF THE USE OF THE CALCULATING RULE
Mensuration, etc.
Screw Cutting
Gearing, etc.
Delivery from Pumps
Power of Steam Engines
THE TRIGONOMETRICAL APPLICATIONS OF THE CALCULATING RULE
The Scale of Sines
The Scale of Tangents
The Scale of Logarithms
It is a somewhat surprising fact that in an age in which such an immense amount of attention is given to labour-saving tools and appliances generally, so little advantage has been taken of the Calculating Rule - an instrument which offers a ready means for mechanically performing all the varied calculations which are required by the engineer or architect, the chemist or the power user.
It must be admitted, however, that latterly the merits of the Calculating Rule have become more generally recognised and its advantages more fully understood, and there is little doubt that the instrument will become much more popular in the future than it has been in the past.
The great improvements effected in the Calculating Rule by the addition of the "runner," as well as by the adoption of a systematic arrangement of the various scales, have done much to encourage the use of the instrument, but a concise and practical handbook explaining its many and varied uses is, however, indispensable to the fullest appreciation of the merits of this useful instrument. This the writer has endeavoured to supply.
The Construction of the Calculating Rule.
The A. W. Faber Calculating Rule consists of a "stock" or "body" about 10 inches in length, 1¼ inches in width and 3/8 inch in thickness. In this stock a groove is formed which carries a moveable strip or "slide," the up.per surface of which is level with that of the stock of the rule. Upon the "face" of the rule thus formed, four scales are engraved, one near the upper edge of the slide being adjacent to a precisely similar one on the upper part of the stock: while another near the lower edge of the slide has adjacent to it a precisely similar scale on the lower part of the stock of the rule.
In close proximity with the face of the rule, the "runner " is arranged to slide freely backwards and forwards. In some instruments the runner consists of a metal strip, bridging over the several scales, and provided with chisel-like projections which lie over the scales, and the edges of which may be brought to any division line of the scales as required.
In the A. W. Faber Rule a form of runner is used which is much to be preferred to the foregoing. This consists of a light metal frame, sliding as before in small grooves formed in the edges of the stock and the rule, and containing a piece of glass about 1 inch square, in the centre of which is a fine black line, which can thus be brought over any division line. One great advantage of this arrangement is that it leaves visible the adjacent graduations of the several scales, thus enabling the operator to readily assign the correct value to the reading sought.
In several other respects this form of runner will be found greatly superior to the more usual form, especially noticeable being the facility with which the settings may be made in complicated calculations.
The A. W. Faber Calculating Rule has usually been made of well-seasoned boxwood. Recently, however, an improved form has been introduced, in which the boxwood body is provided with celluloid facings upon which the several scales of the instrument are engraved. The white surface of the celluloid throws the division lines into more distinct relief than is the case with the all-boxwood construction, and in general it is less fatiguing to the eyes.
The only objection to the celluloid-faced rule is, that this facing material is somewhat unreliable under variations of atmospheric conditions. However, as the graduations of the Calculating Rule are in every case comparative and not absolute, the expansion and contraction cannot affect the accuracy of the instrument.
Reference has already been made to the fact that the face of the Calculating Rule has four scales engraved thereon. The upper one of these, found on the stock of the rule, is usually designated the "A" scale. Immediately adjacent to it is a precisely similar scale on the slide, and known as the "B" scale. On the lower edge of the slide is found the "C" scale, and finally, the precisely similar scale on the lower part of the stock is the "D " scale.
As facility in the use of the Calculating Rule depends in very large measure upon the readiness with which the operator can assign the correct value to each graduation of these several scales, it will be necessary to explain, at some length, the notation and sequence of the several sets of graduations referred to as the "scales."
Taking first the A scale (which as explained is exactly similar in every respect to the B scale), it will be seen that this commences with 1 at the left-hand upper corner of the rule. This is known as the left- hand "index " of the scale. Following the scale along, it will first be noticed that it consists of two similar sets of divisions - the primary divisions of the first half being numbered from 1 to 10, while those of the second or right-hand half of the scale are numbered from 10 to 100.
It will be further noticed that the spaces comprised between the successive primary divisions are of constantly diminishing length. This is in consequence of the fact that the position of each of the several division lines is such that it represents, by its distance from the left-hand index, the logarithm of the number by which it is distinguished. Thus if the whole length 1 to 10 be imagined divided into 1000 equal parts, the graduation marked 2 would be placed at the
301st division, since the logarithm of 2 is ·301. Similarly division line 3 would be placed at the 477th, and line 4 at the 602nd division of the imaginary evenly-divided scale, and so on, the relative distances of the several primary graduations from the index being proportional to the logarithms of the numbers by which they are distinguished.
The same principle determines the positions of the other divisions of this and also of the other scales, while it applies equally to the several sub-divisions of all.
It is well known that the addition of the logarithms of two numbers gives the logarithm of their product, while the subtraction of the logarithm of a smaller number from that of a greater gives the logarithm of the result of dividing the greater number by the lesser.
With the Calculating Rule such lengths of the scales representing various quantities may be readily added to or subtracted from each other by means of the slide. A simple example will best illustrate the method. Thus let it be required to find the result of multiplying 2 by 2. The logarithm of 2 we have first seen is ·301. Adding this to ·301 we obtain ·602, or the logarithm of 4. With the rule we proceed to mechanically effect this addition by drawing the slide to the right until the left-hand index (1) of scale B agrees with 2 on scale
A. Then over 2 on B is found 4 on A. With the slide so set, it is readily perceived that to a length 1 - 2 on A, there has been added a length 1 - 2 on B, the result of which addition is at once read off on A over 2 on B. The same setting of the rule shows that in dividing 4 by ~ 2, we take from a length 1 - 4 (representing 4) on A, a length 1 - 2 (representing 2) on B, the result (2) being read off on A over the left hand index on B.
It is upon this principle that all the operations effected by the Calculating Rule depends, but beyond this rudimentary explanation, no further inquiry into the properties of logarithms need here be entered into.
Reverting again to the several divisions of the upper scales, it will be observed that all the primary spaces as 1 - 2, 2 - 3, 3 - 4 to 90 - 100 are each divided into ten smaller spaces, but since the lengths of the successive primary spaces rapidly diminish, it becomes impossible to sub-divide each of these to the same extent as is possible with 1 - 2 or 10 - 20.
Commencing with the left-hand index (1) of A, and assigning to that division line a value of 1, it will be seen that the first small sub division met with represents 1·02, the second 1·04, and so on until the first main sub-division line marked 1·1 is reached. The same method is pursued until the primary division line 2 is reached. The succeeding primary spaces 2 - 3, 3 - 4, 4 - 5 are each divided into ten parts, each of which is again sub-divided into two parts. Thus in this part of the scale, the space from each successive division line to the next represents an addition of ·05, so that commencing at 2, we should read 2, 2·05, 2·10, 2·15, 2.20, etc., to 4·95 and 5·00. Regarding the primary spaces
5 - 6, 6 - 7, 7 - 8, 8 - 9 and 9 - 10, the rapidly diminishing lengths of these only permit them to be each divided into tenths, so that from 5 the reading is : - 5·1, 5·2, 5·3, etc., to 9·9 and 10·0.
Precisely the same plan of sub-division is adopted in the right- hand half of the upper scales, but in this case every division line is of tenfold value as compared with those just enumerated. Although more minute sub-division of the scales is not possible with this length of rule, it becomes an easy matter to estimate by the eye the further sub-division of the several spaces. With a little practice expertness is soon acquired in correctly reading off any result which falls intermediately of the engraved division lines.
It is highly important that the operator should be able to read the scales with facility, and in this connection he will find Fig. 1 in the accompanying sheets of illustrations of material assistance. In this, the position of the following values are clearly indicated : -
| 1·26 | 1·58 | 1·77 | 1·83 | 1·975 | 2·20 | 2·29 | 2·65 |
| 3·74 | 4·82 | 4·96 | 5·59 | 6·42 | 7·58 | 8·65 | 9·82 |
| 11·2 | 14·4 | 16·9 | 18·3 | 19·75 | 23·0 | 27·2 | 38·7 |
| 46·5 | 48·4 | 52·1 | 59·4 | 67·5 | 81·7 | 94·9 |
Coming now to the lower scales C and D (of which we need only consider the latter, since they are exactly similar), it will be seen that in this case the scale extends from 1 (left-hand index) to 10 (right-hand index). It resembles, therefore, the left-hand half of the A scale, but as it is of twice the length of that scale, the sub-divisions are more numerous and the reading therefore more minute. Commencing at the left-hand index (1) of D, and assigning thereto a value of 1, the first sub-division met with would be read 1·01, the second 1·02, and so on until the first numbered division 1·1 is met, and continuing in this way until the primary graduation 2 is reached. The spaces 2 - 3 and 3 - 4 are each divided into 50 parts, so that the values assigned to these will be 2·02, 2·04, etc., to 3·98 and 4·00. The remainder of the primary spaces of this scale are divided into 20 parts, so that we read 4·05, 4·10, 4·15, etc., to 9·95 and 10. Fig. 2 will assist in rendering this clear, the following values being marked thereon : -
1·25 1·85 2·35 2·58 3·49 4·57 9.34
From the foregoing explanation it will be seen that either the upper scales A and B, or the lower pair C and D may be used for ordinary multiplication, division, proportion, etc. The use of the upper scales has the advantage of enabling a much larger range of values to be read off without a second movement of the slide being necessary. On the other hand, the scales being of only one-half the length of C and D, more accurate results can be read on the latter. Generally, therefore, it may be said that when only approximate results are sought, the upper scales are to be preferred, but when greater exactitude is needed, the lower pair should be employed.
It is important to observe that, when using either pair of scales, the values assigned to the several divisions of the scales depend directly upon the value assigned to the left-hand index figure of the scale. But in such calculations as involve the use of the upper and lower scales in conjunction, the value assigned to the left index figure (1) of the D scale determines the value of all the divisions on the rule.
It must further be clearly understood that although this index figure is designated 1, it may be taken equally to represent any value that is a multiple or submultiple of 10. Thus this left-hand index (1) of the D scale may be regarded as 1, 10, 100, 1000, etc., or as 0·1, 0·01, 0·001, 0·0001, etc.; but once the initial value is assigned to the index, the ratio of value must be maintained throughout the whole scale. For example, if 1 on D is taken to represent 10, the main divisions 2, 3, 4, etc., will be read as 20, 30, 40, etc. On the other hand, if the fourth main division is read as 0·004, then the left index figure of the scale will be read as 0·001. The figured sub-divisions of the main space 1 - 2 are to be read as 11, 12, 13, 14, 15, 16, 17, 18 and 19 if the index represents 10, and as corresponding multiples for any other value of the index.
Independently considered, these remarks apply equally to the A or B scale, but in this case the notation is continued through the second half of the scale, the figures of which are read as tenfold values of the corresponding figures in the first half of the scale. Thus if the left index of A is read as 10, the scale will run 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 (centre index), 200, 300, 400, etc., to 1000 at the right-hand index. The reading of the intermediate divisions will of course be determined by the values assigned to the primary divisions.
Before proceeding to illustrate the methods of using the Calculating Rule, it is desirable to indicate the mathematical relation which exists between the upper and lower scales.
It has been pointed out that each of the two somewhat similar scales, which together form the A scale line, is only one-half the length of the D scale. Therefore, starting at the left-hand index, the actual length representing on the D scale the logarithm of 2, would be twice that representing the logarithm of 2 on the A scale, and so on through out the whole length of the scale. In other words, the lengths representing the logarithms of the numbers on the A scale are, considered comparatively, equal to those on the D scale multiplied by 2, and therefore, from the well-known properties of logarithms, equal to the logarithms of the squares of the numbers on the latter scale. Since the numbers and not the logarithms are engraved on the rule, it consequently results that opposite any number on D, we find its square on A, and, conversely, that under any number on A is its square root on D, this relationship holding for every division on the rule. The runner fitted to the rule enables the coinciding divisions of the upper and lower scales to be accurately determined, while, as will be shown later, it also greatly facilitates operations generally, especially when of a complex character.
On the reverse side of the slide three scales are engraved. To these reference will be made later, when dealing with the trigonometrical applications of the Calculating Rule. It is now only necessary to further note that on one edge of the instrument a scale of inches is provided, while on the other edge is a millimetre scale. This latter, which runs up to 260 millimetres on the edge of the rule, may be continued to 510 millimetres by means of the supplementary scale seen at the bottom of the groove in the rule when the slide is withdrawn. Thus, if a length of 420 millimetres be required, the slide is withdrawn to the right until the left-hand end of it agrees with 42 on the scale inside the groove. The total length from the left-hand end of the stock of the rule to the right-hand extremity of the slide is then 420 millimetres.
Finally, on the back of the Calculating Rule is a comparative scale of inches and millimetres, which enables a ready comparison of the two measures of length to be very readily made.
One of the most simple, but at the same time one of the most important applications of the Calculating Rule, is its use for the solution of problems involving the proportion, or ratio of quantities. As before explained, either the upper or lower pair of scales may be used, depending upon the degree of accuracy required. Assuming the C and D scales to be employed, it will be seen that, with the left-hand indices of C and D placed in coincidence, the ratio existing between all corresponding divisions of these scales is unity (1). If, however, the slide be moved to the right, so that the index of C falls opposite 2 on D, it will be seen that the numbers on D will bear to the coinciding numbers on C a ratio of 2 to 1. The same relationship will obviously exist between the numbers on these two scales no matter in what position the slide may be placed. Hence the rule for proportion which is apparent from the foregoing may be expressed as follows : -
RULE FOR PROPORTION. - Set the first term of a proportion on the C scale to the second term on the D scale, and opposite the third term on the C scale read the fourth term on the D scale.
EXAMPLE 1. What is the fourth term in the proportion 15 : 35 :: 19·5 : x?
Draw the slide to the right until 15 on C coincides with 35 on D, and under 19·5 on C read 45·5 on D, the required fourth term.
It will be noticed that the graduations used in the above example are marked 1·5, 3·5, 1·95 and 4·55 respectively, but as previously explained these engraved values are also to be taken as representing any multiple value thereof, care being taken to give the corresponding multiple value to the result. In this case the engraved figures are increased tenfold; therefore the resulting fourth term is also increased tenfold, being read as 45·5.
This method may be readily modified so as to give from any three known terms of a proportion the remaining term of the expression. Thus, given the 2nd, 3rd and 4th terms of the above example, the method of procedure would be : - Set the 3rd term (19·5) on C to the 4th term (45·5) on D, and opposite the 2nd term (35) on D read the required 1st term (15) on C. All it is necessary to observe is that the 1st and 3rd terms are always found on one scale, and the 2nd and 4th on the other.
It should be noted that as a consequence of the constant proportion existing between the numbers on the two scales, the fraction (1st term)/(2nd term) may be expressed as 1/x or as its reciprocal x/1 , the value of x in the first case being read on the D scale under the index of the slide, and in the second case on the C scale over the index of the D scale. Thus, in reducing vulgar fractions to decimals, the decimal equivalent of 3/16 , for example, is determined by placing 3 on C to 16 on D, when over the index or 1 of D we read 0·1875 on C. In this case the terms are 3 : 16 :: x : 10.
For the inverse operation - to find a vulgar fraction equivalent to a given decimal - the given decimal fraction on C is set to the index of D, and then opposite any numerator on C is found the corresponding denominator of the fraction on D.
If the index of C be placed coincidentally with 3·1416 on D, it will be clear from what has just been said that this ratio exists throughout between the numbers of the two scales. Therefore against any diameter of a circle on C will be found the corresponding circumference on D. As the graduations of the rule, however, do not admit of a very exact setting being made in this way, it has become customary under this and similar circumstances, to set the slide by some more convenient, but still sufficiently exact, equivalent ratio. For example, instead of the value p just given, the ratio 22/7 is fequently adopted.
In the A. W. Faber Calculating Rule a special graduation line will be found on the A and B scales, marking the exact position of p Therefore all that is necessary is to draw the slide to the right until 1 on B is exactly under the line marked p on A. With the rule thus set, the diameters of any circles taken on B will have immediately above them their corresponding circumferences on A.
The ready solution which the Calculating Rule affords of all problems involving ratio or proportion, renders the instrument of peculiar value for determining the equivalent values in different denominations of the various weights, measures, etc.
EXAMPLE 2. Convert centimetres into inches.
As 1 inch is equivalent to 2·54 centimetres, all that is necessary is to place 1 on B to 2·54 on A, as shown in Fig. 3, when above any number of inches on B will be found the equivalent length in centi metres on B, or vice-versa. In the figure the following conversions are noted : -
1·25 inches |
= 3·18 centimetres. |
2·75 inches |
= 6·99 centimetres. |
2·50 inches |
= 6·35 centimetres. |
3·50 inches |
= 8·89 centimetres. |
In the above example the left-hand index of both the A and B scales have a value of 1. Frequently, however, the two scales used in conversions of this kind differ considerably in value, this of course depending upon the value of the two factors which determines the ratio existing between the two denominations. Thus, in converting English miles to metres, or vice versa, the left-hand index of B repre senting 1 mile would be set to 1610 on A, representing the equivalent number of metres. In making this setting, 1 on B is most conveniently set to 1·61 on A, since this enables more of the rule to be used than if the graduation 16·1 is employed. The fact must, however, be borne in mind that while the B scale is read as engraved, all the divisions of the A scale are to be read as of a thousandfold value.
When the C and D scales are used for such conversions, a portion of one scale will project beyond the other. To read this portion of the scale the runner is brought to whichever index (1 or 10) of the C scale, which falls within the rule. The slide is then carefully moved (without disturbing the runner) until the other index of the C scale coincides with the runner. The remainder of the equivalent ratios may then be read off. It must be remembered that if the slide is moved in the direction of notation - that is, to the right, the values read thereon have a tenfold greater value ; while if the slide is moved to the left, the readings thereon are decreased in a tenfold degree.
Inverse Proportion. - In such problems as those in which "more" requires "less" or "less" requires "more," the case is one of inverse proportion, and although from what has been said it will be seen that this form of proportion is quite readily dealt with by the preceding method, it may be observed that the working is simplified to some extent by inverting the slide so that the C scale is adjacent to the A scale. By the aid of the runner the values on the inverted C (written C') scale and on the D scale can be read off. These will now constitute a series of inverse ratios. Thus in the proportion 4 : 3 : : 8 : 1·5, the 4 on the C' scale is brought opposite 3 on D, when under 8 on C' is found 1·5 on D.
Multiplication, which is only a form of proportion in which one of the terms is 1, has next to be considered. The rule for this operation, which will be apparent from the foregoing, is : -
RULE FOR MULTIPLICATION. - Set the index of the B scale to one of the factors
on the A scale, and over the other factor on B read the product on A; or,
set the index of C to one factor on D, and under the other factor on C read
the product on D.
EXAMPLE 3. Multiply 3·5 by 1·3.
Using the upper pair of scales, 1 on B is placed under 3·5 on A, and over 1·3 on B we
read 4·55 on A, as shown in Fig. 4.
EXAMPLE 4. Multiply 135 by 38.
Using the lower pair of scales, and placing 1 on C to 1·35 (read as 135) on D, we read
under 3·8 (read as 38) on C the required product 5·13 (read as 5130) on D.
This example indicates the necessity for taking care to give the correct value to the
result. Rules might be given for locating the position of the decimal point, but these are
cumbersome and not easily remembered.
Generally, it may be said that the number of digits in a product is obvious from the value of the factors, but if any doubt exists, a rough mental calculation can be readily made. Practice soon enables the operator to read off the correct result without hesitation.
In general it will be seen that the extent to which the C and D scales are sub-divided is such as not to enable more than three figures in either factor to be dealt with. For the same reason it is impossible to directly read more than the first three figures of any product, although it is often possible, by mentally dividing the smallest space involved in the reading, to correctly determine the fourth figure of a product. Necessarily this method is only reliable when used in the earlier parts of the C and D scales. However, the last figure of a three-figure, and in some cases the last of a four-figure, product can be readily ascertained by an inspection of the factors.
Thus, in such a case as 700 x 1·69 = 1183, we place 1 on B to
1·69 on A, and find the result on A over 7 on B. This is seen to be more than 11·8 and less than 11·9, but as it is evident that 7 x 9 = 63, it is clear that the final figure is 3 and the correct product is therefore 11·83.
In cases where more than three figures enter into either or both of the factors, the fourth and following figures must be neglected. It should be noted that if the first neglected figure is 5, or greater than 5, it will generally be advisable to increase by 1 the third figure of the factor employed. Generally it will suffice to make this increase in only one of the factors; but it is obvious that in some cases greater accuracy will be obtained by increasing both factors in this way.
The continued multiplication of a number of factors is, by the aid of the runner, very conveniently effected, this being one of the marked advantages over the older forms of the type of rule now under consideration. With the former it is necessary to read off the result of each separate multiplication, the product so found being used as one of the factors in the next operation, this process being repeated until all the factors have been taken into account. With the runner, however, the operation is continuous, so that not only is time saved but much greater accuracy secured, since the errors incidental to the several separate settings are altogether avoided.
EXAMPLE 5. Find the product of 3·2 x 75 x 4·2 x 1·5 = 1512. Using the lower scales, we place the right-hand index of C to 3·2 on D, and bring the runner so that the line thereon is over 75 on C. Bringing the right-hand index of C to the runner line, the latter to 4·2 on C, and the left-hand index of C to the runner, we read under 1·5 on C the required product 1512 on D, the last figure being estimated by the eye.
Division.
As division is merely the inverse of multiplication, we obtain the following : -
RULE FOR DIVISION. Set the divisor on B under the dividend on A, and read the quotient on A over the index of B; or, set the divisor on C over the dividend on D, and read the quotient on D under the index of C.
EXAMPLE 6. Divide 4·55 by 3·5.
Using the upper scales, place 3·5 on B under 4·55 on A, in the manner shown in Fig. 5. Then over 1 on B is read 1·3 on A.
EXAMPLE 7. Divide 76·5 by 4·5.
Here, 4·5 on B is placed to 76·5 on A, as shown in Fig.
6, when over 1 on B is read 17 on A, the required quotient.
Combined Multiplication and Division.
The combination of the rules for multiplication and division as given
in the foregoing is often of Ihe greatest possible service, especially in solving problems
which may be represented by the equation
axb/c = x.
In such a case, the division of a by c is first effected by placing c on C to a on D. Then, without paying any attention to the result of this operation, the multiplication of quotient by b is effected by reading under b on C the required value of x on D.
EXAMPLE 8.
30 x 28·9 / 51 = 17
Setting 51 on C to 30 on D, we read 17 on D, under 28·9 on C.
More complicated cases are such as are represented by : -
(a x b x c x d) / (e x f x g x h) = x.
It is in examples of this kind that the advantage of the runner becomes strikingly apparent, since by its aid, the result of such a lengthy calculation may be readily found without any regard being paid to the intermediate values which result from the successive steps in the operation.
EXAMPLE 9.
(35 x 71 x 17 x 42·8)/(42 x 20 x 5.8 x 8.5) = 43.6
The operations necessary to solve this problem are as follows : - Set 42 on C to 35 on D, and bring the runner to 71 on C. Bring 20 on C to the runner, the runner to 17 on C, 58 on C to runner, the runner to 42·8 on C, and 8·5 on C to runner. Then under the right hand index of C read 43·6 on D.
The position of the decimal point in the answer in such examples as these is best determined by a rough cancellation, which in many cases can be mentally effected.
It will often be found that when the slide has been finally set the result cannot be read off, for the reason that it lies beyond the extremity of the rule, either to the right or left. In such a case, the runner is brought to whichever index of C is available and the slide moved until the other index coincides with the runner, when the result can be read off.
In complex cases of either continued multiplication and division combined, some discrimination should be used as to the sequence in which the various factors are taken into account. It will be frequently found that by taking the factors in a different order from that in which they are presented in the original problem, it is possible to avoid changing the position of the slide as would otherwise be necessary, owing to the reading falling outside the limits of the scale. Obviously, however, it is impossible to give rules for procedure in such cases, as facility in dealing with the factors in the most advantageous manner can only be acquired by practice.
By inverting the slide, as previously explained, so that the C scale lies in contact with the A scale, and setting the slide with the right and left-hand indices coinciding, it will be found that the result of multiplying any number on D by the coincident number on the inverted scale of C (C1), and which is readily effected by the runner, is in all cases equal to 10.
It will further be observed that as a consequence of this, the numbers on the C1 scale are the reciprocals of those coinciding with them on D, and vice versa. Thus 2 on D is found opposite 0·5 on C1; 3 on D opposite to 0·333; while opposite 8 on C1 is 0·125 on D, etc.
It will now be perceived that if we attempt to apply the ordinary rule for multiplication, with the slide inverted, we shall actually be multiplying the one factor taken on D by the reciprocal of the other taken on C1. But multiplying by the reciprocal of a number is equivalent to dividing by that number. Further dividing a factor by the reciprocal of a number is equivalent to multiplying by that number. Hence it follows, that with the slide inverted the operations of multiplication and division are reversed. In multiplying, therefore, with the slide inverted we place (by the aid of the runner) one factor on C1, opposite the factor on D, and read the result on D under either index of C1. It results that with the slide thus set, any pair of coinciding factors on C1 and D will give the same constant product found on D under the index of C1.
It has been previously explained that the relationship which exists between the upper
and lower scales is such that immediately over any number on D will be found its square
on A. Similarly over any number on C will be found its square on B.
Conversely it follows that under any number on A is found its square root on D, and
under any number on B is its square root on C. We have therefore the following : -
RULE FOR SQUARING A NUMBER. Set the runner to the given number on D, and read
off the required square on A under the runner.
In place of the runner the indices of the B and C scales may be employed, if desired,
as shown in Fig. 7.
EXAMPLE 10. Find the square of 93.
Setting the runner to 93 on D, the square is read on A as 8650, the true result being
8649.
EXAMPLE 11. Find the square of 27.
Setting the runner to 27 on D, the square is read on A as 729.
It will be observed that in Example 10 the result is read on the right-hand scale
of A, while in Example 11 it is read on the left-hand scale of A.
In the first case the result is seen to contain twice the number of figures
that the original number contained, while in the second case, the number in the result is
one less than twice that number. This brings us to the : -
RULE FOR NUMBER OF FIGURES IN THE SQUARE OF A NUMBER.
If the result is read on the right-hand scale of A, the number of digits is
equal to twice the number of digits in the original numbers; but if the result is read on
the left-hand scale of A, the number of digits is one less than twice the number in
the original numbers.
In finding the squares of decimals care must be taken in esti mating the number of digits in the number and in the result. Thus : -
EXAMPLE 12. Find the square of ·00405.
Placing the runner to 405 on D, the reading on A is found to be 164 [16405]; but in order
to correctly state the result it must be observed that the number of digits in the
original number is - 2, since two cyphers follow the decimal point. Therefore by the
rule just given the number of digits in the result (since the reading is found on the
right-hand scale of A) is - 2 x 2 = - 4. Therefore the result is
written ·0000164.
EXAMPLE 13. Find the square of ·0155.
Here the result read as 24 will be found on the left-hand scale of A, and the number of
digits it contains will therefore be ( - 1 x 2) - 1 or - 3, so that
the result will be read as ·00024 [·00024025] .
Square Roots : - After what has been said with reference to squaring a number, the procedure in the inverse operation of extract ing the square root will be evident, since it is only necessary to set the runner to the given number on A and to read off the required square root on D under the runner.
EXAMPLE 14. Find the square root of 45·5.
Set the number (or the indices of B and C as shown in Fig. 7) to 45·5 on A, and read
6·74 [6·745+] on D. This operation is shown in Fig. 7.
It must be observed that if the number consists of an odd number of digits, it is to be taken on the left-hand portion of the A scale, and the number of digits in the root is N being the number of digits in the original number. When, however, there is an even number of digits in the given number, it is to be taken on the right hand portion of the A scale, and the root contains one-half the number of digits in the original number.
Mention should be made of another method of extracting the square root, by which more accurate readings may generally be obtained. This involves the use of the C and D scales only. It is preferable to work in this case with the slide inverted, although it can be used with almost equal facility in the ordinary position. If there is an odd number of digits in the number, the right index, or if an even number of digits, the left index of the inverted scale C' is placed so as to coincide with the number on D of which the root is sought. Then by the aid of the runner, the number is found on D which coincides with the same number on C', which number is the root sought.
EXAMPLE 15. Find the square root of 222.
Setting the right hand index of C1 to 222 on D,. it is found that 14·9 is the
number on D which coincides with the same number on C1. This therefore is the
required square root (14·899+).
In raising a number to its third power, the foregoing method of squaring is used in conjunction with ordinary multiplication, the rule being expressed as follows : -
RULE FOR CUBING A NUMBER. Bring the right or left-hand index of C to the given number on D, and over the same number on the left-hand B scale read the required cube on A.
EXAMPLE 16. Find the cube of 1·25.
Set the left-hand index of C to 1·25 on D, and over 1·25 on B read 1·95 on A
[1·953125] .
Fig. 8 shews the position of the slide for this
operation, and it will be noticed that in this case the slide projects to the right.
EXAMPLE 17. Find the cube of 7·25.
In this case the right-hand index of C is set to 7·25 on D, when over 7·25 on B is read
381 on A. This setting of the rule is shown in Fig. 9,
from which it will be seen that the slide in this case projects to the left.
By the above methods of working, four scales are brought into requisition. Of these the D scale and the left-hand scale of B are always employed, and are to be read as of equal denomination; while the final result is read off on the left or right-hand scales of A as the case may be. This method of cubing a number is generally the most satisfactory, although it is sometimes preferable to carry out the operation by continuous multiplication, using the runner in the manner already explained.
In many cases the number of digits in the product is self-evident, but in any case the following rules are sufficient to determine the number of digits in any cube, n being the number of digits in the number, and N the required number in the cube : -
N= 3n - 2 when the product is read on the left-hand scale of A with the slide projecting to the right.
N= 3n - 1 when the product is read on the right-hand scale of A, slide projecting to the right.
N= 3n when the product is read on the left-hand scale ot A with the slide projecting to the left.
With decimals the same rules apply, but, as before, the number of digits must be read as - 1, - 2, etc., when one, two, etc., cyphers, follow immediately after the decimal point.
Thus in Example 16 the result is read on the left-hand scale of A, and with the slide projecting to the right; so that as there is one digit in the number there will be 3 - 2 = 1 digit in the answer, which is therefore read as 1·95.
In Example 17 the result is read on the left-hand scale of A, with the slide projecting
to the left. In this case, therefore, there
will be three digits in the answer, which is consequently read as 381 (381 ·078125) .
Cube Root. - The method of performing the inverse of the fore- going operation, which is necessary in order to obtain the cube root of a number, will now be evident. Employing the same scales as before we have the following : -
RULE FOR EXTRACTING THE CUBE ROOT. Move the slide, either from right to left or from left to right, until under the given number on A is found a number on the left-hand B scale identical with the number which is simultaneously found on D, under the right or left-hand index of C. This number is the required cube root.
But it will be found that by using the four scales mentioned above, it becomes possible, by working in the manner described, to find three values for the root. To decide which of these is the value sought, it is necessary (as in the arithmetical method of extraction) to point off the given number into sections of three figures, commencing at the decimal point and proceeding to the left for numbers greater than unity, and to the right for numbers less than unity. Then if the first section of figures reading from the left consists of 1 figure, the number is to be taken on the left-hand scale of A and the slide is to project to the right. If of 2 figures, the number is to be taken on the right-hand scale of A with the slide to the right. If of 3 figures, the number is to be taken on the left-hand scale of A, the slide projecting to the left.
Therefore in order to find the cube root of 4000, 4, 0·004, 0·000004, etc., 4 on the left-hand scale of A is used with the slide to the right-hand, since these examples evidently fall under the first rule.
For the cube root of 40,000, 40, 0·040, 0·00004, etc., the right- hand scale of A is used with the slide to the right.
And finally for 400,000, 400, 0·400, 0·000400, etc., the left-hand scale of A is used with the slide to the left-hand.
EXAMPLE 18. Find the cube root of 12.
This evidently falls under the second of the above conditions; so bringing the runner to 12 on A, the slide is moved to the right until it is found that when the left hand index (1) of C is over 2·29 on D, 2·29 on B is also under the line on the runner.
The rule for the number of digits in the root will be obvious from these for cubing a number. Thus in the previous example, by adding 1 to the number of digits (2) and dividing by 3, it is seen that the required root must contain 1 digit. It is therefore read as 2·29 [2·289] .
Another method of finding the cube root is indicated in Fig. 10. This involves the use of the inverted slide which, as shown, is placed so that what is now the right-hand index of the slide coincides with the number of which the cube root is sought, in this case 12. It is then necessary to find what number on D coincides with the same number on the inverted scale of B, and this in the case considered is seen to be 2·29, which is therefore the root sought.
EXAMPLE 19. Find by this method the cube root of 130.
The disposition of the rule for the solution of this problem is shown in Fig. 11, from which it will be seen that to the number taken on the left-hand scale of A (since it consists of 3 digits) is placed the left-hand index of the slide, and the number on D, which coincides with a similar number on the inverted scale of B, is seen to be 5·07, which is therefore the required root. It should be noted that when the cube root is found by means of the inverted slide, the latter projects in the opposite direction to that given in the first rule for extracting the cube root.
Since to raise a number to its fourth power it is only necessary to square the square of a number, we have the following : -
RULE FOR RAISING A NUMBER TO THE FOURTH POWER. Set the right or left-hand index of C to the given number on D, and over the number on C read the fourth power on A.
The fourth root of a number may be extracted by reversing the operation, but it is generally preferable to extract the square root of the square root.
Practical Illustrations of the Use of the Calculating Rule.
In the preceding pages general instructions have been given for performing the operations most usually in request. A number of practical examples will now be given in order to exhibit the great utility of the Calculating Rule in a variety of applications.
EXAMPLE 20. Determine the area of a circle 5 3/4 inches diameter.
In order to obtain the area of a circle of diameter d we have the formula, Area = (p/4) d2.
The division of p by 4 is first effected by bringing 4 on B to the line p on A; then, without taking note of the result of this operation, the subsequent multiplication by d2 is performed by reading the result on A over d on C.
Therefore in the example given, set 4 on B to ri on A as in Fig. 12, and over 5·75 on C read by the aid of the runner 26 square inches on A, which is the area required. The true result is 25·967, thus showing that the result obtained is sufficiently accurate for all practical require ments.
EXAMPLE 21. Find the area in square feet of a circle 16 inches in diameter.
In this case the formula becomes
Area = (p d2) / (4 x 144) = (p /576 )d2
Therefore setting 576 on the left-hand scale of B to p on A, as in Fig. 13, we read over 16 on C the area = 1·4 square feet on A.
Problems relating to the solidity or cubic contents of cylinders are readily solved by the aid of the Calculating Rule, special gradua tion lines being marked on the C scale which greatly facilitate calcula tions of this kind.
In order that these special lines may be used intelligently the principle upon which their positions are determined may be profitably explained.
The cubic contents of a cylinder = Sectional area x length
= (p/4) x d2 x l
in which d is the diameter of the cylinder and 1 its length.
But the successive multiplication of p/4 by d2 and then by 1 may be very conveniently avoided by substituting for , its reciprocal, p/4 = 1·273. The formula then becomes
Cubic contents = (d2 x l) / 1.273
in which form the solution of problems of this kind may be readily effected by one setting of the slide. Therefore on C a special line is marked at the position corresponding to 1·237 on B.
EXAMPLE 22. Find the cubic contents of a cylinder 1·24 feet in
diameter and 3·24 feet in length.
Place, as indicated in Fig. 14, the special
graduation line c to 1·24 on D, and over 3·24 on B read 3·91 cubic feet on A as
the required cubic contents.
It will be seen that if the setting of c to the given diameter necessitates the slide being drawn more than one half of its length to the right, it is not possible to read off the contents in the manner described. Thus, if the given diameter was 6·15 inches and the length 36·5 inches, the setting of the slide as above directed would show the slide projecting too far to the right to enable the result to be read off.. For this reason, therefore, a supplementary graduation marked ci is given on the C scale, the distance between the marks c and ci being equal to that from 1 to 10 on the upper scales. It will be understood that in using the graduation ci the result is to be diminished tenfold, since it is clear that the slide has been moved back to such an extent as to cause all the readings between the upper scales to be one- tenth of their correct value.
EXAMPLE 23. Find the cubic contents of a cylinder 6·15 inches in
diameter and 36·5 inches in length.
Set the special graduation line or "gauge point" ci to 6·15 on D, as shown in Fig. 15, and over 36·5 on B read 1084 cubic inches
on A.
EXAMPLE 24. Find the contents in cubic inches of a pipe 4·8 inches in
diameter and 34 inches long.
Set, as in Fig. 16, the line C to 4·8 on D and
over 3·4 (read 34) on B, read 615 cubic inches on A.
The determination of the number of digits in the answer in such
problems is most expeditiously effected by a rough mental calculation. The methodical
manner of deciding this point would be as follows, taking Example 24 as an illustration :
-
Setting gauge point c on C to 4·8 on D we obtain 4.82 /
1.273 on A
over 1 on B. Reading over 3·4 on B, we should obtain 61·5 on A; but as the reading on B
is, by the conditions of the problem, increased tenfold, we must likewise increase the
reading of A tenfold, and there fore over 34 on B, read 615 on A.
Screw Cutting.
As already pointed out, the Calculating Rule is particularly serviceable in all calculations involving the proportion or ratio existing between various quantities. One of the most useful practical illustrations of this application of the instrument is found in solving problems relating to screw cutting and the determination of the change wheels necessary to cut a screw of given pitch.
EXAMPLE 25. In a lathe, the guide screw of which is of ½ inch pitch, it is required to cut a thread of 3/16 inch pitch. If a wheel containing 45 teeth is placed on the mandrel, what wheel must be used on the guide screw to cut the required thread, and what other pairs of wheels may be alternatively used if desired?
In this case if m be the number of teeth in the wheel on the
mandrel, and s the number of teeth in the required guide screw wheel, the ratio m/s
must be such that
(m/s) x ½ = 3/16
or m/s = 3/8
Therefore setting 8 on B to 3 on A, as in Fig. 17,
the required ratio is so established that under any mandrel wheel on A is found the
corresponding wheel for the leading screw on B.
Then as the wheel on the mandrel has 45 teeth, it is seen that the required wheel for the leading screw must contain 120 teeth.
Other pairs of wheels which will produce the required screw are seen to be 15/40 30/80 and 60/160 if the teeth in the change wheels are multiples of 5. Failing this restriction we have 21/56 27/72 36/96 etc., as other sets of wheels which will cut the thread required.
EXAMPLE 26. Determine the circumference in feet of a pulley
27·5 inches in diameter.
In this case, the circumference of a circle 27·5 inches in diameter is to be divided by
12. Therefore set 12 on B to the special line marked p on
A, as shown in Fig. 18, and over 27·5 on B read
7·2 feet on A.
EXAMPLE 27. What is the speed of a belt which runs on a pulley 17
inches in diameter, when the latter makes 50 revolutions per minute?
Set 12 on B top on A, and bring the runner to 17 on B.
Then bring the right-hand index of B to the runner, and over 50 on B read 222·5 feet on A
as the required belt speed.
EXAMPLE 28. A pulley 5 feet in diameter, running at 225 revolutions per
minute, drives by a belt another pulley 3 feet 7 inches in diameter. Find the revolutions
of the latter per minute.
Problems of this kind are most readily dealt with by inverting the slide as shown in Fig. 19. Setting 60 on C1 to 225 on D, by
the aid of the runner it will be found that under 43 on C1 is 314 on D, this
being the required number of revolutions of the small pulley.
EXAMPLE 29. A spur wheel, 11 feet 5 inches in diameter at the pitch
line, has 230 teeth. Find the pitch of the teeth.
Reducing the pitch diameter to inches (137), it is then only necessary to multiply by p (the ratio of the circumference of a circle to its diameter) and
divide by 230.
Therefore, as indicated in Fig. 20, set 230 on B
to 137 on A, and over the special graduation p on B read
1·87 inches on A as the required pitch.
EXAMPLE 30. The velocity of a belt 8 inches in width is 4000 feet per
minute. Find the horse power it will transmit, allowing an effective tension of 50 lbs.
per inch of width.
In this case we have -
Horse Power = Velocity x tension x width /
33000
which in the above example becomes -
Horse Power = (4000 x 50 x 8)/ 33000 =
(4000 x 8) / 660
Therefore set 660 on B to 4000 on A (Fig. 21),
and over 8 on B read 48·5 on A, the required horse power.
It will be understood that with the slide so placed, the power
transmitted by any width of belt at the given tension may be read off on A above the belt
width on B.
EXAMPLE 31. Required the diameters of two spur wheels, one of which is to make 7
revolutions while the other makes 8, and the distance apart of their centres is 5 feet.
Set 7 + 8 = 15 on C to 120 on D, as shown in Fig.
22, and under 7 and 8 on C read 56 and 64 inches as the respective diameters on D.
EXAMPLE 32. Find the horse power which can be transmitted by a spur
wheel 5 feet in diameter and 3 inches pitch, when running at 70 revolutions per minute,
assuming that
Horse Power = (pitch)2 x diam. in
inches x revolutions / 400
which in the above example becomes -
Horse Power = 32 x 60 x 70 / 400
Set 400 on B to 3 on D, as shown in Fig. 23, and
bring the runner to 60 on B. Then bring 1 on B to the runner, and over 70 revolutions on B
read 94·5 horse power on A, as shown in Fig. 24.
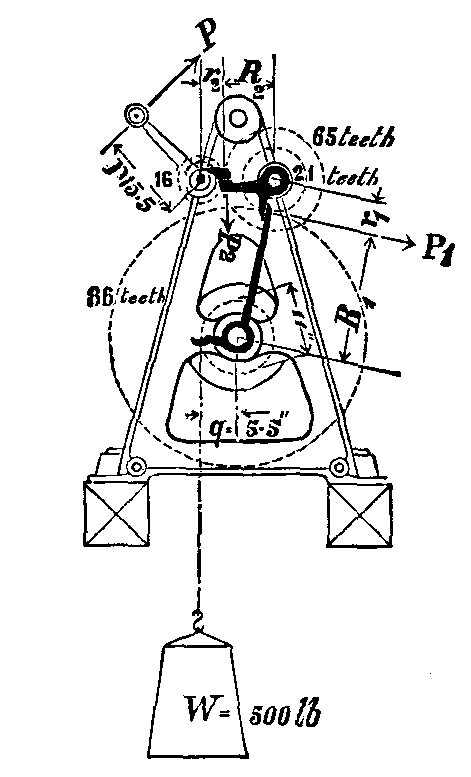
EXAMPLE 33. As an example of the more complicated problems which may be readily solved by
the aid of the Calculating Rule, we take the hand winch shown in the accompanying cut, and
proceed to determine the power P which must be applied at the handle in order to raise a
weight of 500 lbs., friction being neglected. The relative proportions of the gearing are
shown in the sketch.

The hand lever P, 15·5 inches in length, turns a pinion of 16 teeth, which gears with a wheel of 65 teeth. On the same shaft as the latter, is a pinion of 21 teeth gearing with a wheel of 86 teeth on the barrel shaft. The barrel is 11 inches in diameter. The thick lines in the diagram show very clearly the effective leverages which are acting.
Designating by P and W the power and weight respectively, and by R1
r1 R2 and r2 the radii of the wheels, it will
be seen that
(1) The pressure on the teeth at P1 = W x q / r1
(2) The pressure on the teeth at P2 = P1
x r1 / R2
(3) The power applied at the handle = P = P2 x r1
/ R2
From this it follows that
P=W x (q/p) x (r1 / R1) x (r2
/ R2)
and as we may substitute the number of the teeth in the wheels for their radii, we have
P=500 x (5.5/15.5) x (21/86) x (16/65)
The manner in which this calculation is effected is shown by the successive positions of the slide and runner in Figs. 25 to 28.
As indicated in Fig. 25, the slide is first set so that 1 on B coincides with 5 (read 500) on A, and the runner set so that the line thereon agrees with 5·5 on B. The product of 500 x 5·5 could now be read off on A under the runner line, but this intermediate result is not read but is at once divided by 15·5, by bringing this latter on B to agree with the runner as shewn in Fig. 26.
The result of this operation (500 x 5.5) / 15.5 could now be read off on A over 1 on B,
but instead, it is multiplied by 21 by bringing the runner to the position shown. Bringing
86 on the slide to the runner, as shown in Fig. 27,
effects the succeeding division, and placing the runner to agree with 16 on B, and moving
the slide so that 65 on B coincides with the runner, as in Fig. 23, the result may be read
off on A over 1 on B.
From this it is seen that
P = (500 x 5.5 x 21 x 16) / (15.5 x 86 x 65) =
10.66 lbs
EXAMPLE 84. Find the horse power transmitted by a steel shaft 5 inches in diameter at
75 revolutions per minute, from
H.P. = (d2 N) / 80
in which d is the diameter in inches, and N the number of revolutions per minute.
Set 10 on C to the diameter (5) on D as shewn in Fig.
29, and bring runner to 5 on B. Next bring the divisor 60 to the runner, and over 75
on B read 156 H.P. on A (Fig. 30). The true
result is 156·25.
Delivery from Pumps, etc.
EXAMPLE 35. Find the amount of water in gallons theoretically delivered per stroke by a
pump 6 inches in diameter and 1·2 feet stroke.
Set 29·4 on B to 6 on D by the aid of the runner (Fig.
31), and over 1·2 on B read 1·47 gallons per stroke on A.
[ N.B - 1 / 29·4 = (p/4) x (12/277) ]
In practice a suitable allowance must be made for slip and other losses of efficiency.
EXAMPLE 36. Find the theoretical velocity of water flowing under a head of 55 feet.
Set 100 on B to 55 on A as in Fig. 32, and under
64·4 on B read 59·5 feet per second on D as the required velocity.
In this and similar cases in which the right-hand index of B must be used in place of the left-hand index, it must be understood that results on A being diminished one hundredfold, readings on D are to be increased tenfold. Thus in the last example the reading on D is 5·95, but as the conditions of the problem render necessary the use of the right-hand index (100) of B, the result is increased tenfold and is read as 59·5.
EXAMPLE 37. Find the indicated horse power of an engine in which the cylinder diameter (d)
= 18 inches; the stroke (s) = 2 feet; the mean effective pressure in lbs. per square
inch (p) = 40; and the number of revolutions per minute (n) = 60.
The usual formula for this calculation is
I.H.P. = d2 x ·7854 x s x 2 x n x p /
33000
an expression which may be conveniently changed to
I.H.P. = d2 x s
x n x p / 21000
To find the indicated horse power in the above example, 21000 on B is set to the cylinder diameter (18) on D as shewn in Fig. 33, and the runner brought to agree with the stroke in feet (2) on B. Then 1 on B is brought to the runner (Fig. 34) and the latter to the revolutions per minute (60) on B. 1 on B is then brought to the runner, and over the mean effective pressure (40) on B is read the required I.H.P. = 74 on A (Fig. 35).
EXAMPLE 38. Find the tractive force of a locomotive having driving
wheels 54 inches in diameter, and cylinders 18 inches in diameter, with a stroke of 24
inches.
Set 54 on B to 18 on D as in Fig. 36, and over 24
on B read 144 on A as the tractive force in lbs. for each lb. of mean effective pressure
on the piston.
The Trigonometrical Applications of the Calculating Rule.
On the under side of the slide of the Calculating Rule will be found three scales. The upper of these, marked 5, is the Scale of Sines, and is used to determine the natural sines of angles of from 35 minutes to 90 degrees. The notation of this scale will be evident on inspection. The main divisions 1, 2, 3, etc., represent the degrees of angles; but the values of the sub-divisions differ according to their position on the scale. Thus if any primary space is sub-divided into 12 parts, each of the latter will be read as five minutes (5').
In order to determine the sine of an angle by the aid of the Calculating Rule, the slide is withdrawn from the stock of the instru ment and re-inserted in such a manner that the scale marked S lies adjacent to the A scale of the rule, and with the right and left-hand indices coinciding.
With the slide so placed, the sine of any angle may be read off on the A scale, immediately above the angle on the scale S. Fig. 37 gives a number of examples which will serve to illustrate the method of procedure, the following readings being marked thereon : -
| Between 1 and 10 of the A scale | Between 10 and 100 of the A Scale | |||
| Sine 0°40' | = 0·0116 | Sine 6° | = 0·1045 | |
| Sine 1° | = 0·0175 | Sine 7°30' | = 0·1305 | |
| Sine 1°50' | = 0·0319 | Sine 9°50' | = 0·1707 | |
| Sine 2°10' | = 0·0378 | Sine 12°20' | = 0·214 | |
| Sine 3° | = 0·0523 | Sine 15° | = 0·259 | |
| Sine 3°20' | = 0·0581 | Sine 21°30' | = 0·367 | |
| Sine 4°20' | = 0·0756 | Sine 30° | = 0·500 | |
| Sine 5° | = 0·0872 | Sine 56° | = 0·829 | |
| Sine 5°40' | = 0·0987 | Sine 74° | = 0·961 | |
It must be carefully noted that the value of the sines ot all angles read on tbe first half of the A scale, i.e. between 1 and 10, are such that the decimal point is always followed by 0; while those read on the right-hand half of the A scale, between 10 and 100, are prefixed by the decimal point only. This will be evident from the example shown in Fig. 37.
The method of calculating with the sine scale is precisely similar to that already explained in the preceding pages. A few illustrations will, however, serve to exemplify the many varied uses which can be made of the instrument for trigonometrical calculations.
EXAMPLE 39. Find the product of 38 x sine Placing 1 of the sine scale
under 38 on A, as shown in Fig. 38,
the product is found above the line representing the angle 5°50' on the sine scale. The
required product is then read off as 3·86.
EXAMPLE 40. Find the product of 7·4 x sine 15° (see Fig. 39). In this case the result cannot be directly read off, as it
falls
beyond the rule. It is therefore necessary to proceed as previously explained, by placing
the right-hand index of S to 7·4 on A, when over 15° on S is read 1·917 on A.
EXAMPLE 41. Find the result of dividing 20 by sine 5°40'.
As shown in Fig. 40, 5°40' on the S scale is
placed to 20 on scale A, and over the left-hand index of S is read 202·6, the required
quotient.
EXAMPLE 42. Given, two angles of a triangle,
a = 20°30'
b = 45° ;
also, the length of the side opposite to the angle b
b = 75
find the length of the side a, opposite to the angle a
The formula for this is : -
a = 75 sine 20°30'
/ sine 45°
Therefore in order to solve this problem, the line representing 45° on scale S is placed so as to agree with 75 on A, and the result, 37·15 = length of side a will be found on A, over 20°30' on S (Fig. 41).
Another method of determining the sines of angles may be employed, in which the reversal of the slide is avoided. It will be found that the back of the rule has a recess or aperture at the right- hand extremity, and that upon the edges of this are index lines. By the aid of the upper one of these, the sines of angles may be found in the following manner : -
Draw out the slide (Fig. 42) until the angle on the sine scale 5, coincides with the index line in the aperture. If the rule is now turned face upwards, the required sine will be found on B, under 100 on A. For example, sine 2°30' = 0.0437. Also:-
sine 79° = 0.982
sine 60° = 0.866
sine 28° = 0.469
sine 13° = 0.2249
sine 6° = 0.1045
sine 2° = 0.0349
In this case (Fig. 43) the sine of 20° is found as before on the A scale opposite 20° on the S scale of the reversed slide, the value being read 0·342. The runner is then brought to this value on the D scale and the value of sine2 20° is read off on A at the runner line. This is found to be 0·1169.
When the sine is known and the corresponding angle is to be ascertained, the mode of
operating will be evident from the foregoing, and further explanation is therefore
unnecessary.
The Scale of Tangents.
The lowest of the three scales on the reverse of the slide is marked T, and is used for determining the tangents of given angles.
The method employed is very similar to that used for finding the sines, the slide being reversed and re-inserted as before. The respec tive tangents of the angles marked on scale T may then be read off on scale D.
It should be noted, however, that only those tangents which are between 0·1 and 1 can be directly read off, these limiting values corresponding to angles between 5° 43' and 45°.
In Fig. 44 the following values are shown : -
| tangent 6°20' | = 0·1109 | tangent 25°. | = 0·4663 | |
| tangent 7° | = 0·1228 | tangent 27°40' | = 0·5243 | |
| tangent 9°50' | = 0·1733 | tangent 30° | = 0·5774 | |
| tangent 13° | = 0·2309 | tangent 37°30' | = 0·7673 | |
| tangent 18°30' | = 0·3346 | tangent 40°10' | = 0·8441 | |
| tangent 20°10' | = 0·3673 | tangent 44°30' | = 0·9827 |
If the angle whose tangent is required is greater than 45°, the method of operation is modified in the manner illustrated by the example given in Figs. 45 and 46.
EXAMPLE 44. Find tan. 60°.
For this we have :- tan. 60° = 1 / tan (90° - 60°) = 1 / tan 30° = 1 / 0.5774 =
1·732.
EXAMPLE 45. Find 240 x tan. 60°.
Here, 240 x tan. 60° = 240 / tan 30° = 240 / 0.5774 = 415.5
The various calculations in which the tangents of angles are involved are carried out in
the same way as described in connection with the calculations involving the sines of
angles.
The tangents of angles less than 5°43' cannot be read directly from the rule, but the
corresponding sines may be substituted for them without material error, as the discrepancy
only affects the fourth decimal place. Thus
tan. 1°10' = sin. 1°10' = 0·020361
tan. 3°40' = 0·06408. Sin. 3°40' = 0·063952
When large numbers have to be multiplied, the discrepancy arising from this method becomes more serious, but in the case of angles between 3°30' and 5°43' it may be corrected by adding to the sine of the angle, 3 per cent. of the value of the sine. By this correction a sufficiently exact value of the tangent is obtained.
The evenly-divided scale found in the centre of the reverse side of the slide and marked L, enables the logarithms of numbers to be found. It must be observed, however, that only the mantissa of the logarithm can be read off, the characteristic being determined by the following rule : -
The characteristic of a logarithm is equal to the number of digits in the number, minus 1. If the number is wholly decimal, the index is equal to the number of ciphers following the decimal point plus 1. In the latter case the characteristic is negative, and is so distinguished by having the minus sign written over it.
The method of determining the logarithm of a given number is as follows : -
Referring to Fig. 47, the left-hand index of the
C scale is set to the given number on the D scale. The rule is then turned over and the
mantissa of the logarithm read on L at the index line in the aperture at the right-hand
end of the rule. Thus -
| log. 358 | = 2·554 | log. 35·8 | = 1·554 | |
| log. 0·358 | = 1·554 | log. 0·0358 | = 2·554 |
The number corresponding to a given logarithm may be readily determined by a reversal of the above method.
Higher Powers and Roots. - One of the most useful applications of this method of obtaining the logarithms of numbers is found in determining powers and roots other than squares and cubes. Any power or root may in this way be very readily determined, the method to be followed being illustrated by the following example : -
EXAMPLE 46. Find 7Ö 1893. (See Figs. 48 and 49.)
Proceeding as above directed, it is found that log. 1893 = 3·277, and by the rule for
division it is found that = 0·468. Setting 468 on the scale of logarithms to the index
line in the aperture, the number corresponding to log. 0·468 is found to be 2·94, this
being found on the scale D under the left-band index of the C scale.Therefore
7Ö1893 = 2·94.