THE “OMNES” RULE

The provision of a spare slide (see Fig. 15) enables this new “all metal” Rule to practically combine in itself all the best features of the “Gravet,” “Fix,” “Rietz,” “Jackson Log-log,” “Faber,” and “C.E.M.” Slide Rules.

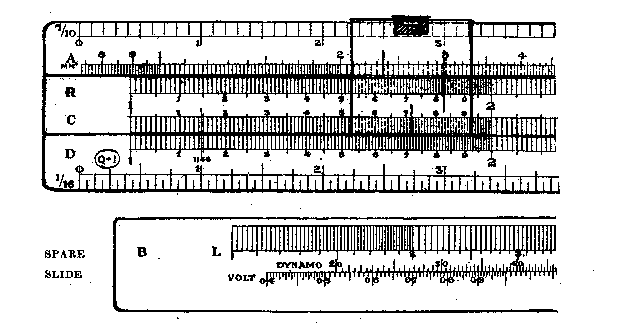
FIG. 15. PATENT ALL-METAL “OMNES” RULE

As in the regular “Gravet” Rule, so in the “Omnes” Slide Rule, all ordinary calculating (multiplication, division, etc.) is done on scales C and D; sines and tangents are read on scales A and D respectively by turning the slide over and setting scale S to scale A, or scale T to scale D, as required; logarithms are read opposite index-mark at back of Rule, working in conjunction with scale D.

Scale B, however, is relegated to the spare slide, and its place on the normal slide is taken by a root scale (marked R), which is really a repetition of scale C. From this arrangement it follows (1) that when scales A and R are set so that the end divisions (marked 1) exactly coincide, we have in these two scales a complete table of squares and square roots, from which squares (on A), or roots (on R), can be read at will, without any manipulation of either slide or cursor; and (2) that when the end divisions of scale R are both set to 7854 on scale A, these two scales then form tables of areas and diameters of circles enabling direct readings of areas (on scale A) and corresponding diameters (on R) to be made with the greatest facility.

Direct readings of cubes and cube roots are obtained by substituting the spare slide for the normal one and setting the “Rietz” or “cubes” scale to scale D. The same position of the spare slide converts the Rule into a “Jackson” log-log Rule, enabling log-log calculations to be performed precisely.

Other scales provided on the spare slide are the B scale (marked also L and KW) and two scales marked respectively “Dynamo, Motor” and “Volt Loss.”

The “dynamo” scale (20 to 100) and the “motor” scale (100 to 20) are used in conjunction with scales A and B (conveniently remarked for this purpose HP and KW) for determining the efficiency of dynamos and electric motors. The relative positions of these four scales are such that if the effective H.P. on scale HP is set against the electrical power in kilowatts on scale KW, then the corresponding efficiency of the motor or dynamo can be read off—opposite to 1 of HP scale—on the “motor” or “dynamo” scale as the case may be.

Conversely, of course, by setting 1 of HP scale opposite to the known efficiency the scales KW and HP become comparative scales (or “tables”) from which can be read off all possible corresponding relative values of the electrical and brake powers.

EXAMPLES

Determine the relative values of the electrical and brake powers of a certain type and make of dynamo, of which the efficiency is 80%— Set 80 of the “dynamo” scale opposite 1 of HP scale (using the cursor line to project across); then against 20 horse-power read 11.94 kilowatts, against 450 HP read 29.84 KW, and so on. Again, what is the efficiency of a dynamo which delivers 90 KW and absorbs 150 HP Set 90 of KW scale to 150 on HP scale; then opposite 1 of HP scale read the answer (= 8.4%) on the “dynamo” scale, using cursor-line. Again, find the efficiency of an electric motor which gives 16 BHP for an expenditure of 25 kilowatts: Set 25 of KW scale to 16 on HP scale; then, opposite 1 of the HP scale read the answer (47.7%) on the “motor” scale, using the cursor for projecting across. Conversely, given that the efficiency of an electric motor is 74.6%, find the relative BHP and KW: Set 1 of HP scale opposite 74.6 on the “motor” scale; then at 20 HP read 20KW, at 50 HP read 50KW, and so on.

The “Volt” scale enables calculations on the “fall of potential” in electric circuits to be performed easily and quickly.

For a simple copper lead, either with direct current or with alternating current free from induction, the following formula holds good—

        V = (L x A) / (q x c)

where V = fall of potential or “drop” in volts; single length of lead in metres; A = current strength in amperes; q = sectional area (in sq. mm.) of copper; and c = a copper conductivity constant, which in graduating the “volt” scale of the Rule has been taken at 28.57.

Having given any three of the variables V, L, A, and q, the fourth one is obtainable by one setting of the, slide, in conjunction with the “volt” scale and cursor-line, as will be readily understood by the following examples. It cannot, however, be too carefully noted that the operations are only applicable for direct currents, or for induction-free alternating currents.

EXAMPLES

Determine the loss of potential in a copper lead of 180 metres length and 45 sq. mm. section, for current strengths of 20, 30, and 50 amperes: Note, first, that to facilitate these electrical calculations the normal scales A and B have special designations given to them. Thus normal scale A (which serves both for “ampere” scale and “sectional area” scale) is marked also mm.2, and normal scale B becomes “single length of lead” scale and is re-marked L. Then, set 45 of “sectional area” (mm.2) scale to 18 (180) on scale L, and read the answers (= 2.8, 4.2, and 7.0 volts respectively) on the “volt” scale opposite 20, 30, and 50 on the “ampere” scale (A) using cursor-line to project across. Again, a copper lead 1500 metres long is desired to have a “drop” of 10 volts with a current strength of 20 amperes; find the necessary copper section: Bring 10 on the “volt” scale opposite 20 on the “ampere” scale, using the cursor-line; then, opposite 1.5 (1500) on scale L, read the answer (= 105 sq. mm.) on scale mm. Conversely, if in the last example the copper section available was only 95 sq. mm., determine the “single length of lead to suit: With exactly the same setting read the reduced “length of lead” (= 1360 metres nearly) on scale L, opposite 95 on scale mm.2

Return to Omnes rule in Collection