
| Slide rules HOME page | INSTRUCTIONS | A-to-Z |
Decimal point
Approximate calculation
Rules based on
the position of the slide relative to the stock
Rules based on the position of the answer
Decimal tracking scales
Scientific notation
The principal scales on a slide rule are generally numbered 1, 2, 3 ... to 10, or 1, 2, 3 ... to 1, however the use of slide rules is not limited to this range of values. The number, say, 1.5 can also represent 15 or 150 or .15 etc.. When you multiply and/or divide by a series of numbers it is not always obvious where the decimal point should be. There four ways of estimating the position of the decimal point in the answer:
For each of these we look at three sample cases: multiplication, division and combined multiplication & division. In some cases the explanation is trivial but in others it it gets quite complicated.
We also look at the use of scientific notation.
Example: Multiplication
To calculate 3.57 * 8.12. On the slide rule this would be calculated as 3.47 * 8.12 and
the answer would be 2.82. The above numbers can be considered approximately as 4 * 8 which
is 32, so we know the correct answer is 28.2 and not 2.82 or 282.
Example: Division
To calculate 405 / 0.71. On the slide rule this would be calculated as 4.05 / 7.1 and the
answer would be 5.70. By approximation this could be considered as 400 / 1 which is 400,
so we know the answer is 570.
Example: Combined multiplication and division
To calculate 3.57 * 100.5 * 0.12 / (27.9 * 83.1). Using the markings on the rule, this
would be treated as:3.57 * 1.005 * 1.2 / (2.79 * 8.31). The answer on the slide rule would
be "1.86" but the decimal point may or may not be correct. The above calculation
can be approximated as: 4 * 100 * .1 / (30*80) = 40/2400 = 1/60 = .0167. In the above
case, the answer would be 0.0186.
This method has a number of advantages the other do not:
- With a complex calculations you can repeat the check (e.g. with
different approximations) without having to repeat the whole calculation,
- If the answer of the check calculation is not at all the same as the
first calculation it may indicate an error using the slide rule,
- Accuracy is increased if you use the CI (inverse), CF and DF (folded)
scales as less slide movement and index changing are involved. There are, as far as I
know, no equivalents to the rules below for these types of scales. This is perhaps the
most important reason of all for using this method.
See also the section on "Scientific Notation" below.
Rules based on the position of the slide relative to the stock
Number of digits
For this method and the following it is necessary to understand what is meant by the "number of digits". In the case of numbers greater than one it refers to the numbers of digits to the left of the decimal point. For example 1.23 has 1 digit and 250, which could written as 250.0, has three. In the case of numbers less than one the "number of digits is negative and refers to the number of zeros after the decimal point. For example 0.13 has zero digits and 0.0045 has -2 digits.
Rule for multiplication
If the rule is set with the slide protruding at the left-hand end of the stock, the number
of digits in the answer is the sum of the digits of the factors. If the slide is
protruding at the right-hand end, the number of digits in the product is one less than the
sum of the digits of the factors.
Rule for division
If, when dividing, the slide protrudes at the left-hand end of the stock, the number of
digits in the result is found by subtracting the number of digits in the divisor from the
number in the dividend. If the slide protrudes to the right the number of digits in the
result will be one greater that the difference between the numbers of digits in the
dividend and divisor respectively.
Rules for combined multiplication and division
When it is possible to carry out two operations at one slide setting you may
disregard the position of the slide, i.e. whether to the right hand or left hand of the
stock, since if the digits have to be added or subtracted they will be equal and of
opposite signs and consequently cancel each other out. It is only when the slide protrudes
to the right and either multiplication or division is effected separately that the number
of digits in the result is affected.
Example: Multiplication
To calculate 3.57 * 8.12. The slide protrudes to the left of the rule. The sum of
the number of digits is 1 + 1 =2. By applying the above rule the number of digits in the
answer must be 2, so the answer is 28.2.
To calculate 3.57 * 12.0. The slide protrudes to the right. The sum of the digits is 1 + 2 = 3. By applying the above rule the number of digits in the answer must be 2, so the answer is 42.8.
Example: Division
To calculate 405 / 0.71. The slide protrudes to the left. The sum of the digits is 3 - 0 =
0. By applying the above rule the number of digits in the answer must be 3, so the answer
is 507.
To calculate .062 / 36.0. The slide protrudes to the right. The sum of the digits is -1 - 2 = -3. By applying the above rule number of digits in the answer must be 2, so the answer is .00172.
Example: Combined multiplication and division
To calculate 3.57 * 100.5 * 0.12 / (27.9 * 83.1). We will perform these in the order
(3.57/27.9) * (100.5/83.1) * 0.12, that is alternating multiplication and division as is
standard practice. A experienced user might vary the order to minimise the number of
movements. The number of digits is 1 + 3 + 0 - 2 -2 = 0
| Calculation | Operation | Slide position | Digit adjustment |
| 3.57 / 27.9 | Division | Right | +1 |
| * 100.5 | Multiplication | No change - so cancel | -1 |
| / 83.1 | Division | Left | 0 |
| * .12 | Multiplication | Right | -1 |
| Balance | 0 | ||
| Number of digits in products/factors | 0 | ||
| Number of digits in answer | 0 |
Let's try another example: 75.1 * 0.57 * 127.0 / (.003 * 821) but in the order of all the multiplications first and then all the divisions.
| Calculation | Operation | Slide position | Digit adjustment |
| 75.1 * 0.57 | Multiplication | Left | 0 |
| 127.0 | Multiplication | Right | -1 |
| /0.003 | Division | Right - no change so cancel | +1 |
| /821 | Division | Left | 0 |
| Balance | 0 | ||
| Number of digits in products/factors | 2 + 0 + 3 -(-2) - 3 = 4 | ||
| Number of digits in answer | 4 |
So the answer is 2210.
Rules based on the position of the answer
Rule for multiplication
If the answer is to the left of the first factor the answer has the number of digits of
the sum of the digits of the two factors. If the answer is to the right of the first
factor the answer has the number of digits of the sum of the digits of the two factors
minus 1.
Rule for division
If the answer is to the left of the first dividend the answer has the number of digits of
the difference of the digits of the two numbers plus 1. If the answer is to the right of
the dividend the answer has the number of digits of the difference of the digits.
Example: Multiplication
To calculate 3.57 * 8.12. The answer is to the left of the first factor. The sum of
the number of digits is 1 + 1 =2. By applying the above rule the number of digits in the
answer must be 2, so the answer is 28.2.
To calculate 3.57 * 12.0. The answer is to the right of the first factor. The sum of the digits is 1 + 2 = 3. By applying the above rule the number of digits in the answer must be 2, so the answer is 42.8.
Example: Division
To calculate 405 / 0.71. The answer is to the right of the dividend. The sum of the digits
is 3 - 0 = 0. By applying the above rule the number of digits in the answer must be 3, so
the answer is 507.
To calculate .062 / 36.0. The answer is to the left of the dividend. The sum of the digits is -1 - 2 = -3. By applying the above rule number of digits in the answer must be 2, so the answer is .00172.
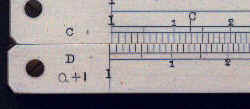
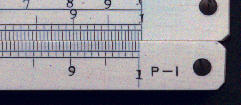
Aids to use of the above
As an aid to the above some early rules had the following marks on the left and right hand
end of the rules. The Q+1 at the left hand signifies that if the answer (i.e. Quotient) is
to the left, one has to be added to the difference; the P-1 signifies that if the answer
(i.e. Product) is to the right then one has to be subtracted from the sum. The third
symbol was the same at both ends of the rule.
 |
 |
 |
Faber Castell also introduced a slide rule with a "digit registering cursor" to help the above method. This is shown below, the idea was to move the counter on the cursor to keep track of the movements. The rules were only produced for about 10 years in the early 20th century so it appears that the idea did not catch on.

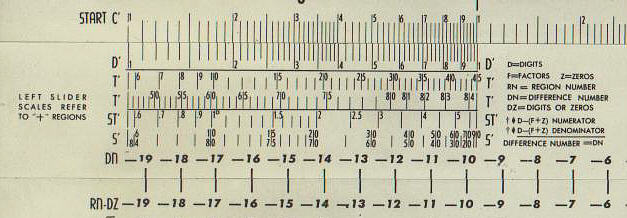
Some makers also produced special scales which covered several log cycles. The idea with these scales was that the calculation would be performed once with the special scales, to get the order of magnitude correct, and then with with C and D scales to get the answer to a higher degrees of accuracy. Whilst these scales were found on general purpose rules, Pickett 901 and 904 for example, they were also found on electronic rules where order of magnitudes could vary considerably and where the user would not have an intuitive feel for the scale of the answer.
The first figure shows these scales for the Pickett Decipoint which not only reproduces the C and D scales but also the trig scales as well.
Although these special scales were never very popular on standard rules they were more common on electronic rules, where the magnitude of the answer could vary greatly. The example below comes from a Graphoplex Electronicien, a French electronics rule.
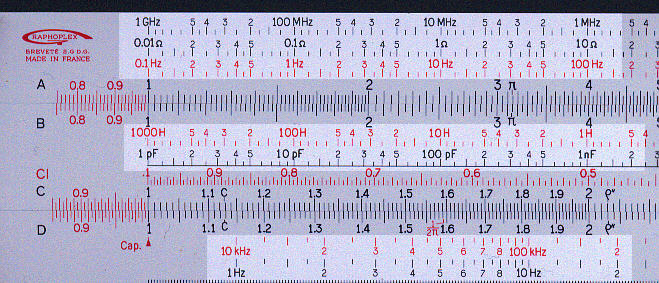
The scales highlighted above cover the following ranges:
| Location | Variable | Range | No. of cycles | Notes |
| Upper part of stock | ||||
| Frequency | 1GHz to 0.1 Hz | 10 | Used with capacitance scale | |
| Resistance | 0.01 W to 100 MW | 10 | Used with capacitance scale | |
| Frequency | 0.1 Hz to 1GHz | 10 | Used with inductance scale | |
| Slide | Inductance | 1000 H to 0.1 mH | 10 | |
| Capacitance | 1 pF to 10 000mF | 10 | ||
| Lower part of stock | ||||
| Frequency | 10 KHz to 500 MHz | 4.5 | Effectively the root of the 10 cycle scales. | |
| Frequency | 1 Hz to 50 KHz | 4.5 | Effectively the root of the 10 cycle scales. |
For more information on this and other electronics rules see the electronics section of this web site.
In scientific notation every number is expressed as a a number between 1 and 10 followed by 10 raised to a power. For example, 86400 (the number of seconds in a day) can be written as 8.64 * 104 or 0.03937 (the number of inches in a millimetre) can be written as 3.937 * 10-2. For slide rule use this is very convenient as all the numbers you use are in the range of the slide rule scales. You still have to do an approximate calculation but since the range of numbers is more limited there is less chance of error.
As an example, which would be familiar to any hydrologist, the average flow during a month is 1.73 m3/sec for a river basin whose drainage area is 176 km2. The rainfall over the basin was 80.7 mm. What percentage of the rainfall became runoff. The basic method is:
Percentage = 100 * 1.73 m3/sec * 86400 sec/day * 31 day/month /(176 km2 * (106 m2 /km2 ) * 80.7 mm * 10-3 m/mm) [All converted to metres]
= 102 * 1.73 * 8.64 * 104 * 3.1 * 101 / (1.76 * 102 * 106 * 8.07*101 * 10-3 )
= (1.73 * 8.64 * 3.1 / (1.76 *8.07 ) ) * (107 / 106)
= 3.26 * 101 [by approximation (2 * 8 * 3) / (2 * 8) = 3 ) ]
=32.6 %
As you can see, for numbers which cover a large magnitude the use of scientific notation plus the approximation method works well and is easy to apply.