Detail - front left |
Detail - front right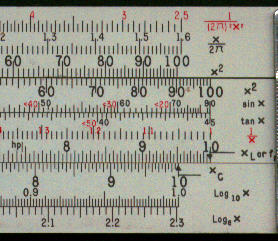 |
Detail - decimal finder scales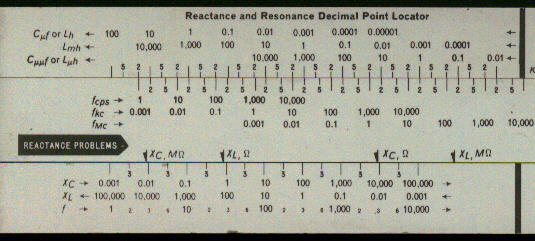 |
|
| Slide rules HOME page | INSTRUCTIONS | A-to-Z |
Electronic slide rules
Introduction
A number of slide rule were produced to aid electronic calculations. (This has always struck me as rather ironic since it was the development of electronic calculators which led to the demise of slide rules). These instructions are based on four rules:
Graphoplex Electronicien - for which I have the summary instructions.
Pickett N-515 Electronic - for which I have no instructions.
Pickett N-531 - Cleveland Institute of Electronics- for which I have no instructions.
Keuffel and Esser - Cooke Radio Slide Rule - for which I have the instructions but not the
rule.
Fortunately there is a degree of overlap between the functionality of the rules so from the information available it has been possible to work out how the rules can be used. The task has been simplified by the fact that whilst all the rules have special scales all of the calculations they describe could be carried with a normal slide rule.
The special scales are used for two main purposes:
1. Since the range of values of electronic parameters (frequency, impedance, etc) is large it is not possible to develop an intuitive feel for the range of the results and therefore it is easier than in other professional fields to make an error in placement of the decimal point. Some of the rules have two sets of scales, one covering several logarithmic cycles (for an approximate answer but with the order of magnitude clearly defined) and one covering one or two cycles (for the answer to be calculated to a higher degree of precision).
2. To facilitate calculations for certain standard formulae. For example the ratio 1/ 2p appears frequently.
Given that there is considerable overlap in the functions to be performed it is hoped that these instructions will be useful with other electronic rules.
The order of these instructions follows, roughly, that of the training manuals in that I describe certain formulae and then how the answer can be calculated with each of the rules identifying any differences between them.
The rules
The Pickett N515 (Cleveland Institute of Electronics)
On the front face the rule has two special scales. The first, labelled (fX) 2p, runs from 1.6 to 1.6 and actually represents the value on the D scale divided by 2p ( x/2p ). The second, labelled (LG) H, runs from 2.5 to 2.5, and represents 1 divided by the value of the D scale times 2 times p squared ( 1/(2px)2 ). On the back there are decimal finder scales. These cover 10 logarithmic cycles and can be used to get answers to the correct order of magnitude. There is one scale on the upper part of the stock, another on the lower part of the stock and two on the slide, the one shown for reactance and another for resonance. In both cases these scales have to be used with gauge points.
Detail - front left |
Detail - front right |
Detail - decimal finder scales |
|
Pickett N531 (Capitol Radio Engineering Institute)
This rule has one special scale, labelled 2p. This runs from 1.6 to 1.6 and, as with the equivalent scale on the above rule, represents the value on the D scale divided by 2p ( x/2p ).
Detail - front left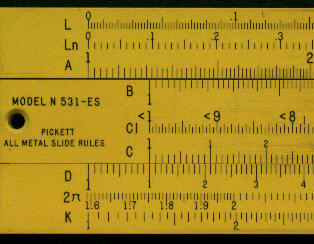 |
Graphoplex Electronicien
This French made rule has on the front a standard set of scales including trig and log-log scales. On the back it has a set of decimal finder scales, in this case also covering 10 log cycles. These are used to get answers to the correct order of magnitude. To get answers to higher degree of accuracy then the other (standard) scales are used with gauge marks (see the 1/2p mark highlighted below).
Detail - back left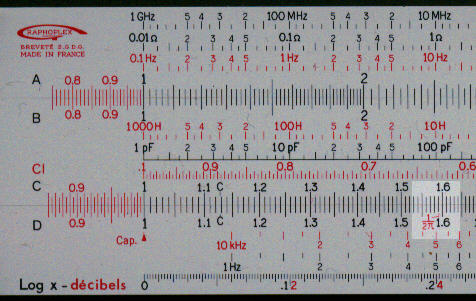 |
Detail - back right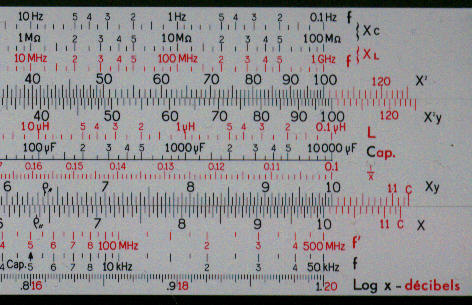 |
This rules comes with a summary set of instructions which I have.
The Cooke Radio Slide Rule
Whilst I do not own this rule I do have a copy of the manual. This rule has the same two special scales as the Pickett N515, in this case labelled 2p and LC.
Power
Not strictly an electronic calculation perhaps but certainly an electrical one.
The basic formula is:
P = I2R
where:
P = power in Watts
I = current Amperes
R = Effective resistance in Ohms.
This can be solved easily on any slide rule using the standard scales.
Method
Set the Index of the C scale against the current (I) on the D scale. Move the cursor to
the resistance on the B scale. Read the power (P) on the A scale.
Example:
C10 to 8.5 D
Cursor to 5.3 B
Answer (383 watts) under cursor on A.
Inductive reactance (XL)
The formula is:
XL = 2pFL
Where:
XL = Inductive reactance.
F = Frequency in cycles per second.
L = Inductance in Henrys
This can of course be solved easily by a standard slide rule. If you have a 2p scale (K&E and Picketts) then:
Method
Cursor to Frequency on 2p scale, inductance on CI scale,
read XL opposite index on C.
Example
What is the inductive reactance (XL) of an AC circuit of 0.08 Henry, if the
frequency is 60 cycles.
Cursor to 60 Hz on 2p scale.
0.08 H on CI to cursor
Answer (30.2 ohms) on D.

On the Graphoplex and the Pickett N515 you can perform a preliminary calculation to get the order of magnitude correct.
Method
Cursor to frequency, Capacitance to cursor, read answer next to XL gauge
mark.
Example
What is the inductive reactance (XL) of an AC circuit of 150 mH , if the frequency is 2 MHz.
Cursor to 2 MHz on f{XL scale.
500 mH on L to cursor.
Answer ( 6300 ohms) on XL scale opposite XL gauge mark
This shows the solution on the Graphoplex.
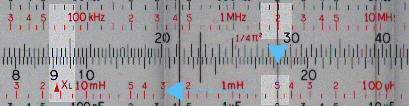
This shows the solution on the Pickett N515, note that you have to be careful what numbers you assign to the scale.

On the Graphoplex, which has a gauge mark for 1/2p, the frequency of 1.8 MHz is set gauge mark and the answer of 5080 ohms on the C scale is read against the inductance of of 450 mH on the D scale. The same calculation can be performed on almost any slide rule.

Capacitive reactance
The formula is:
XC = 1/2pFC
Where:
XC = Capacitive reactance.
F = Frequency in cycles per second.
C = Capacitance in Farads
On a rule with a 2p scale.
Method
Cursor to frequency on 2p scale, capacitance on CI to cursor,
read XC opposite index on D.
Example
What is the capacitive reactance (XC) of an AC circuit of 25mF and a frequency of 13 cycles.
Cursor to 25 on 2p scale.
13 on CI to cursor.
Answer (490 ohms) on C scale against index of D scale.

On the Graphoplex and the Pickett N515 you can perform a preliminary calculation to get the order of magnitude correct.
Method
Cursor to frequency, Capacitance to cursor, read answer next to XC gauge
mark.
Example
What is the capacitive reactance of an AC circuit of 250nF and a frequency of 60
cycles.
Cursor to 60 cycles on XC scale.
250mF on C scale to cursor.
Answer 10600 ohms on XC scale opposite XC gauge mark.
This shows the solution on the Graphoplex.

This shows the solution on the Pickett N515. The 25 part of the capacitance of 250nH is taken from stock just above the slide. The magnitude of .25mF (=250nF) is taken from upper of the three scales (labelled CmF). The frequency, 60 cycles, is taken in a similar way but using the fcps scale. The answer is given as 0.011 Mw which is equal to 11000 ohms.

On the Graphoplex, which has a gauge mark for 1/2p, the accurate answer can be found easily by setting the frequency, 60 cycles, on the C scale to the 1/2p on the D scale and reading the result, 10610 ohms, on the D scale against the capacitance, 250 nH, on the CI scale. This method could of course be used on any rule with a CI scale.

Resonance
If a circuit contains both inductance and capacitance it will resonate a particular frequency given by the equation:
F = 1 / 2p Ö(LC)
where:
F = frequency in cycles per second (Hz)
L = inductance
C = capacitance
For any particular frequency, F, the product of the inductance and the capacitance, LC, is fixed. So if frequency and either inductance or capacitance is given the other value can be calculated.
The Pickett N-515 and the Keuffel and Esser Cooke Radio Rule both have special scales for this. In the case of the N-515 it is labelled (LG H) at one end and l/((2p)2X2) at the other. In the case of the Coke Radio Rule is labelled LC. In both cases, the value on the special scale is equal to l/((2p)2X2) where X is the value on the D scale. One difference between the rules is in the units. In the case of the Cooke Radio Rule the units are Kilocycle for frequency, microHenrys for inductance and microFarads for Capacity. In the case of the N-515 the LC (i.e. D) scale effectively runs from 0.01 to 0.1.
To find the resonant frequency on the N515-T or the Cooke Radio Rule.
Method
Multiply the capacitance by the inductance. Against the product on the LC scale read the answer on the D scale.
Example
What is the resonant frequency of a circuit with a capacitance of 2mF
and an inductance of 5mH.
The product of 2 and 5 is 10.
Against the value of 10 on the LC scale read 5.03 on the D scale.
The magnitude has to be assigned by an approximate calculation or by an use of the
extended scales if available.

To find the resonant frequency on the Graphoplex.
Method
Capacitance on the B scale to the 1/(4p2) gauge mark. Resonant frequency on the CI scale opposite the inductance of the A scale.
Example
What is the resonant frequency of a circuit with a capacitance of 2mF
and an inductance of 5mH.
Place the value of the capacitance (2mF) on the B scale against
the gauge mark 1/(4p2) on the A scale.
Read the answer on the CI (.503) against the inductance 5mH on
the A . This gives you the significant figures only. You either have to perform an
approximate calculation or use the decimal point finder scales, see below.

To perform an approximate calculation on the N-515
Method
Against the capacitance on the Cmf (or appropriate value depending on magnitude) set the inductance on the Lmh (or appropriate value depending on magnitude). Read the frequency on the f scale against the fkC (or appropriate value depending on magnitude) gauge mark.
Example
What is the resonant frequency of a circuit with a capacitance of 2mF
and an inductance of 5mH.
Against the capacitance (2mF) on the Cmf
scale set the inductance (5mH) from the Lmh
scale.
Read the answer, 50 000 Hz on the f scale.
Note:
1. Depending on the range the capacitance can be set on the stock and the inductance on
the slide or vice versa.
2. Since the capacitance and inductance are multiplied, the scale on the slide runs in the
opposite direction to that on the stock.

To perform an approximate calculation on the Graphoplex
Method
Opposite the Cap gauge mark on the f scale set the capacitance on the Cap scale. Read the answer of the f scale against the inductance of the L scale.
Example
What is the resonant frequency of a circuit with a capacitance of 2mF and an inductance of 5mH.
Opposite the Cap gauge mark on the f (frequency scale) set the
capacitance, 2mF, on the Cap scale.
Against the inductance, 5mH, read the frequency (50 000
Hz) on the f scale.
