| Slide rules HOME page | INSTRUCTIONS | CONTENTS |
SECTION FOURTEEN
OTHER CALCULATING INSTRUMENTS
Cylindrical Calculators - Circular Calculators - Watch type Calculators - Other Rules.
In order to accommodate long logarithmic scales, and with a view to securing a higher degree of accuracy, various devices are employed. We cannot proceed with a lengthy description of the instruments which are available; the reader will see them illustrated in catalogues of mathematical instruments, but we will make a short reference to the principles employed.
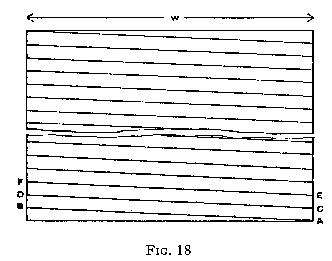
Let us visualise a logarithmic scale in the form of the diagram illustrated in Fig. 18. The graduations commence at A and run in a sloping direction to B, continue from C to D, and then from E to F, and so on. B and C are identical points in the scale, as also are D and E. The total length of the scale is the sum of all the sloping lines. This flat scale is glued on to a cylindrical stock whose circumference exactly equals the width W of the rectangle, and the sloping lines now form a continuous helix, the point B joining up with C, D with E, etc.

In some instruments the total length of the scale is 500" i.e. 50 times the length of scale of a standard slide rule, and the degree of accuracy attainable is high. The instrument is operated by means of adjustable pointers, which may be set to any desired points on the scale, and then moved together to other positions. If the reader will take a pair of dividers and set them to, say, the distance between 1 and 3 on the D scale of his slide rule, then move them so that the left-hand leg is placed at 2, the right-hand leg will register with the 6. This is the fundamental method of multiplication of 2 x 3 = 6, and in principle it is the method used in the cylindrical calculator employing the helical scale.
In other cylindrical instruments the scale runs in sections in the axial direction, and is used in conjunction with a grid surrounding the main cylinder.
The reader will understand that it is easy to set out the C and D scales of his slide rule in circular instead of rectilinear form. Fig. 19 shows, slightly reduced in size, a simple form of circular calculator in which the C and D scales are still 10" in length, but being in circular form, result in a more compact instrument.
The reference letters A, B, C, D and E mentioned in the description, allude to the five circular scales taken in order from outer to inner.
Scale E is for evaluating squares and square roots; scale B deals similarly with cubes and cube roots, and the outer scale A gives a means of finding common logarithms. The cursor takes the form of a transparent sector, rotating about the centre, on which is drawn a radial hair line.
Multiplication is effected by rotating a knob at the back of the instrument, to bring the 1 of D into coincidence with one of the factors in C; opposite the second factor in D the product will be found in C. These operations are exactly analogous to the movement of the slide of the ordinary slide rule. Division, and combined multiplication and division, follow the same general rules applicable to slide rules. Squares and square roots, cubes and cube roots, and logarithms, are found by projecting by means of the rotating cursor from the appropriate scale, to the C or D scales, and vice versa.
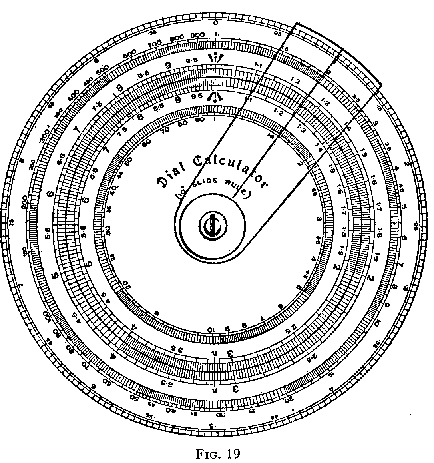
Fig. 20 shows a circular calculator in which the main scale is 50" long. This scale occupies five concentric circles; if the numbering is followed progressively round the five circles starting at 1 in the smallest circle, and proceeding clockwise until the 10 in the fifth circle is reached, no difficulty in passing from one circle to the next will be encountered. Short lengths of bridging scales are provided to assist. The outermost scale is evenly divided and this, in conjunction with the main scale, gives mantissae of common logarithms.
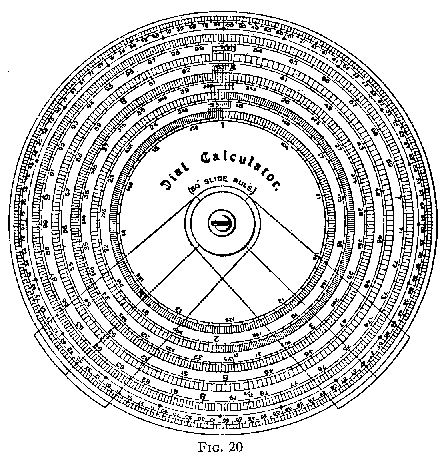
Multiplication is effected by setting the first cursor to the 1 of the main scale and the second cursor to one of the factors in the main scale. By means of a knob at the back of the instrument the two cursors are moved together to bring the first cursor to the second factor, and the product appears coincident with the second cursor. The cursors intersect all five circles, and care is necessary in selecting the correct scale in which to read the result.
Circular calculators resembling pocket watches in size and shape are available. In principle they resemble the two calculators illustrated in Figs. 19 and 20, but they are operated by small spindles equipped with milled heads, similar to the winding mechanism of a watch.
Circular calculators have one advantage over the ordinary type of slide rule; the result is never off the scale, and there is nothing equivalent to traversing the slide to change over from one index to the other; they are also more convenient for carrying in the pocket.
For general convenience in working, and for speed in operation, the ordinary type of slide rule is altogether superior to the circular or cylindrical types, and when the novelty of working with the latter has worn off, the user almost invariably discards the instrument and reverts to the use of his slide rule.
The rules we have described, and the various combinations of scales we have dealt with, do not exhaust our subject. We have attempted to deal with two aspects only; firstly, to teach the rudiments of the simple slide rule to those who previously were unacquainted with them, and to stress the argument that proficiency can be attained easily; secondly, to convince those who use only the standard type of rule that they are employing an instrument of limited utility, and that other rules are available which, whilst retaining the best points of the standard rule, have other features which increase the efficiency of the instrument.
It is quite probable that the reader will occasionally see a slide rule which is equipped with one or more scales which we have not mentioned. As stated above, we do not claim to have covered completely the subject in this small book, but we think we have dealt with the most useful scales. We have made no attempt to deal with the large variety of special slide rules designed for effecting computations related to specific industries. Such slide rules (which are often used for advertising purposes) shorten the work connected with specific problems, but computations effected with their aid may usually be carried out by the ordinary types of slide rule.
© Hodder Stoughton, reproduced with permission.