| Slide rules HOME page | INSTRUCTIONS | CONTENTS |
SECTION TWELVE
THE BRIGHTON RULE
Log-log scale - Sine and tangent scales - Sine scale - Tan scale - X3 scale - L scale - Pythagoras scale
The manufacturers of slide rules are confronted with a variety of difficulties quite separate from those connected with production.
Production problems are almost confined to the difficulty of securing first-class materials.
During the war period and for several years after, timber and plastics, which are the principal raw materials of manufacture of most types of slide rules, were of very poor quality and often gave rise to difficulties in production.
Apart from the initial seasoning of materials, slide rules undergo a further period of seasoning when partly made.
Final inspection is the last process carried out by every reputable manufacturer of slide rules. Each rule is subjected to a critical examination just before despatch from the factory, and any which shows a defect is returned to the production line for rectification. However, it may be six months or much more before the rule reaches the user, in the meantime having been in transit to a distant overseas customer or having lain in stock or some wholesale or retail establishment. The rule may have been displayed in the retailer’s shop window exposed to sun- light or damp conditions and then passed on to the purchaser.
A slide rule is unlike most manufactured products in so far as it can be quickly checked against itself. The first test to apply is to line up the slide in its mid-position and to check the lengths of the C and D scales, which should be identical. Next, if the rule is equipped with A, B, C and D scales, the slide should be set so that the 1 of B is coincident with the 10 of A, then check to see if the 10 of B lines up accurately with the 100 of A. The observant reader will notice a number of similar tests. If there are perceptible discrepancies the rule has suffered some deterioration since it left the factory. If complaint of inaccuracy is made to the source of supply, the rule will almost always be returned to the manufacturer for replacement. All manufacturers are from time to time called upon to make replacements, but in the normal course of business this is not a very serious item. It has the good effect of keeping a high standard of production in the factory and some control over the activities of the distributing agents.
Another kind of difficulty sometimes facing the producer is to satisfy the requirements of the overseas purchasing organisations in respect of the arrangement of scales on a slide rule. Frequently an overseas merchant will refuse a particular type of slide rule because the scales are not quite the same as those with which he is familiar. Sometimes the difference is quite unimportant and may only be a matter of a different arrangement of the same set of scales. Purchasing agencies in the United States of America are usually most insistent that the rule they require must have certain scales arranged in a particular manner, and although there is no difficulty involved to redesigning a slide rule, an undue variety of rules is apt to cause confusion and to hamper production.
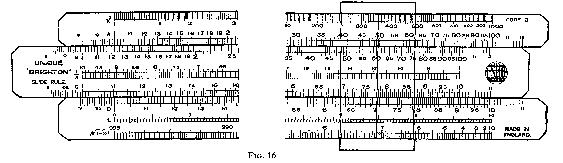
The Brighton slide rule, Fig. 16, which is the subject of this section, was designed to meet the requirements of one of the Continental countries whose purchasing agents demanded a specific arrangement of scales. There is nothing which makes it more suitable for one country than for any other.
The scale equipment is very extensive. All the well-known scales are included, viz:
Scales A, B, C and D.
Reciprocal scale. Reference 1/X.
Cubes and Cube Roots scale. Reference X3.
Logarithmic scale. Reference L.
| Sine scale. | Reference S | } | These scales are subdivided in decimals |
| Tan scale. | Reference T |
Three-section log-log scale. References LL1, LL2,LL3.
Pythagoras scale. Reference Ö(1-x2) , or Py.
Linear scale in cms.
Fig. 16 shows the face of the rule. The linear scale and the sin and tan scales are on the edges of the rule and the log-log scale on the reverse of the slide. The data slip on the back of the rule gives all the useful trigonometrical formulae and there is a decimal equivalent table which shows when the slide is withdrawn.

The three-section log-log scale in the Brighton rule has been extensively dealt with in Section 11 and needs no further mention.
These appear on the edge of the rule and are read by means of a small index attached to the cursor. Instead of being sub- divided in minutes, these two scales are subdivided in decimals of degrees. Both sine and tan scales are used in conjunction with scale D.
Since sin 2A + cos 2A = 1, it follows that the values of sin A and cos A will be found in D and Py respectively if the cursor index is set to A in the sin scale. (Example — set cursor to 30° and find ·5 in D and ·866 in Py.)
Line up the slide so that scales C and D coincide. By projecting from the T scale, the tangent and cotangent appear in D and 1/X respectively. (Example—tan 13·4° = ·238 and cotangent 13·4 = 4·2.)
Numbers in D are cubed when projected into X3. Cube roots of numbers are found by projecting from X3 into D.
The mantissae of common logs of the numbers in D appear directly below in L. (Example — log 2 = ·3010.)
All these scales have been dealt with in earlier sections of this book, with the exception of the Pythagoras scale, and very brief mentions are made here.
Scales A, B, C and D are the subjects of Sections 4 and 5.
The reciprocal scale is fully discussed in Section 10.
The cubes and cube roots scale is dealt with in Section 5.It will be
seen in Fig. 16 as the scale lying along the upper edge of the stock.
The log scale is mentioned in Section 3. With its aid the mantissae of
common logarithms are obtained by projecting the numbers in scale D into scale L, e.g. 2D
projected by the cursor index into scale L gives ·3010.
The Pythagoras scale is an important addition. With its aid, time is saved in solving right-angled triangles, and there are many examples in technical problems and in dealing with vector quantities when it can be used with advantage.
As a matter of interest let us time ourselves in solving a simple problem in the usual way and by using the slide rule equipped with the Pythagoras scale. We will call this scale Py for ease of expression.
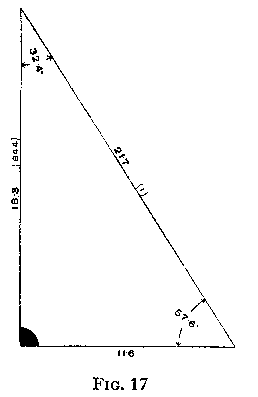
Example: In a right-angled triangle the hypotenuse is 21·7” long and one other side is 18·3” long. We desire to find the remaining side and angles. (See Fig. 17.)
| Square | 21·7 | using C and D scales | = 470 |
" |
18·3 | " |
= 335 |
Subtract |
135 |
Extract sq. root of 135 = 11·6.
tan x = 11·6/18·3 = ·633.
x = 32·4°, y = 90 - 32·4° = 57·6°.
Results:
Side = 116
Angles = 32.4° and 57.6°.
If the reader will work through this first method, writing down only the necessary figures, he will probably require about 2 minutes. We used scales C and D in squaring and extracting sq. root for the sake of accuracy. A little time could perhaps be saved by using scales A and D, but the employment of the 5” scales would be a disadvantage.
Solutions using the Py scale:
Divide 18·3 by 21·7 using C and D, which gives 844.
Move X to 844 in Py.
Set l0C to X.
Under 217C read 1165D.
Under X read 32·4° in S.
Other angle 90 - 324 = 57·6°.
Time taken, under 1 minute.
© Hodder Stoughton, reproduced with permission.