| Slide rules HOME page | INSTRUCTIONS | CONTENTS |
SECTION NINE
THE PRECISION RULE
The Special C & D Scales - Multiplication - Division - Determining in which scale lies the answer.
THE reader will appreciate that the degree of accuracy with which computations may be made with a slide rule depends primarily upon the length of the scales employed, and because of this we have consistently stressed the importance of using C and D scales in preference to the A and B scales for ordinary work.
Obviously, if we used a slide rule with 20" scales, our result should be more precise than when we use a 5" or 10" rule. 20" slide rules are frequently to be seen in drawing-offices, and occasionally even larger rules, up to 40" length, are encountered. These rules are rather awkward to use, but in operation they are no different from the 10" rule.

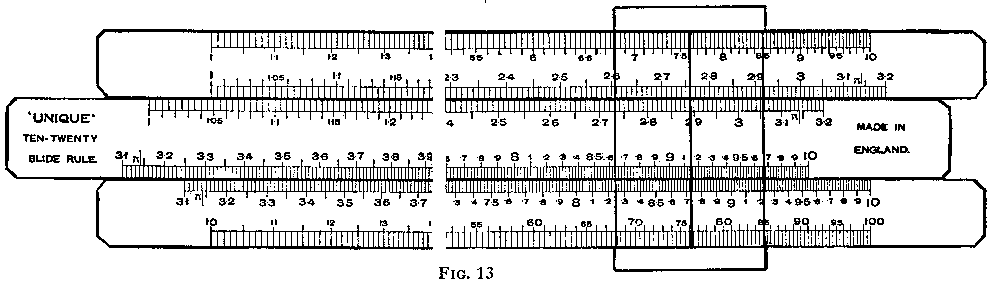
The type of slide rule which employs scales twice the length of the rule, i.e. 20" scales on a 10" stock, or 10" scales on a 5"stock, is not so well known as it should be. The 10/20 rule illustrated (reduced size) in Fig. 13 gives the same degree of accuracy as the 20" slide rule, and is more convenient to use. The illustration shows the additional dividing rendered possible by the longer scale. The C and D scales are divided into two halves, the parts running from 1 to 3·2 occupy the usual positions of the A and B scales and the remainder from 31 to 10 lie in the normal C and D scale positions. The 1 to 10 part of the A scale, doubled in length, is moved to the top edge of the stock, and the 10 to 100 half to the lower edge of the stock.
Multiplication and division are effected by the C and D scales, employing the principles which apply to the ordinary type of rule, but since the graduations on either edge of the slide cannot be brought directly into contact with graduations on the opposite part of the stock, the cursor must be used to bridge across the slide when necessary, and herein lies the only disadvantage of this form of rule. The expert user of a slide rule should find no difficulty. Any uncertainty in deciding on which part of the stock the result lies will be removed, if the following simple maxim is remembered: If when setting the slide it is necessary to use the cursor to cross the slide, it will also be necessary to use the cursor to re-cross the slide, when reading the result.
This maxim is easy to apply when two factors only are involved, e.g. a simple multiplication, or a simple division, and it can be extended to more complex operations.
We have the feeling that the Precision rule suffers in popularity because of the little extra trouble involved in keeping check on the position of the result, but if our work is of such a nature that we can profitably take advantage of the higher degree of accuracy of which the rule admits, we think any prejudice should be removed, and we will therefore give a few examples of the methods we use for keeping check.
For reference purposes we designate that part of the C scale which lies along the upper edge of the slide by c, and the remainder of this scale lying along the lower edge of the slide by C. Similarly, the upper and lower parts of the D scale will be denoted by d and D respectively. These reference letters do not appear in Fig. 13. They should be added as shown in Fig.14.
We will first take a simple example, 11 x 12 x 2. The result, which we can calculate mentally, is 264.
Set lc to lld. X to 12c. lc to X.
Result: 264 in d above 2c.
In this example all the readings lie in the c and d scales, and there is no complication, the operations following one another as with the ordinary C and D scales. The reader will see that in multiplying, say, 9 x 8 x 5 = 360, the operations are all effected in the C and D parts of the scales, and again there is no complication.
Now let us multiply 2 x 7 = 14. If we set 1c to 2d the result is off the scale, so we must set l0C. to 2d, and in doing so we must use X to cross the slide. We move X to 7C and we find the result 14 in d, if we use the cursor to cross the slide again. If we read the result in D we obtain an erroneous answer, and we must guard against this. The reader will see that if we read the result on the wrong side of the slide, it will be about 3 times too large or too small, and often this will disclose the error.
In a longer computation, the Precision rule would be a source of danger if we had no easy way of keeping check on which side of the slide to read the result. We should, of course, always make an approximation, and by doing so determine position of decimal point, or we can adopt the method we will now explain.
Example: Evaluate (1.8 x 6·1 x 108)/(409 x 32·1)
| Set X to 18d | and jot down | T. |
| 409C to X | " | B. |
| Xto6lC | " | B. |
| 321C to X | " | B. |
| X to 108c | " | T. |
Now the cursor index X in its final position registers 286 in d and 904 in D, and we must determine which is the appropriate result. The T we first jotted down indicates that we commence in the top c and d scales by selecting the 18 in d, and the B's indicate that in the second, third and fourth operations the relevant factors were found in the lower C and D scales; the final T means that the last factor was found in the top scale.
In jotting down these letters we should write them horizontally, and after the first T write the remainder in pairs, thus: T BB BT. Each pair of different letters indicates that the result moves from one side of the slide to the other. When the letters of a pair are the same, i.e. two TT's or two BB's, the operations they govern do not move the result across the slide, and in checking off we ignore such pairs. In our example the first factor appeared in the upper scales, the BB we ignore, and the BT indicates we must cross the slide to the bottom scales, and the result, 904, lies there.
A longer example might result in the following sequence:
T BB TB BT TT BT BB TB TT TB, and to reduce this we first strike out the BB and TT pairs; we are then left with T TB BT BT TB TB. Now since each TB or BT indicates crossing the slide, we may cancel these out in pairs, and this will reduce the symbols to T TB, indicating the result is on the opposite side of the slide from the first factor, that is to say, in D.
If the reader will work through a few examples he will find it an easy matter to make the check. There is no necessity to trace the result in its transition from side to side of the slide as the operations are made; it is difficult to do so. Having set X to the first factor, we move the slide or cursor to the other factors in turn, noting the T or B for each operation, and finally we cancel out as shown above to ascertain if the result lies in D or d.
We soon find that it is unnecessary to write down all the T and B signs we have used above. Every operation of multiplication or division, or combined division-multiplication, involves two factors and two movements:
For multiplication - Setting 1 or 10 of the slide scale,
followed by setting X to a factor.
For division - Setting factor in slide scale, followed by setting X to 1 or
10 of slide scale.
For division-multiplication - Setting factor in slide scale to X followed by
moving X to another factor in the slide scale.
If in any operation both factors lie on the same edge of the slide scale - and directly we use the first factor we can see if such is the case - we know that we have a TT or BB to sum up, and we do not even trouble to write them down. We are left with the necessity of recording cases in which the two factors lie on opposite edges of the slide scale. The first time this occurs we write a stroke thus: /, and the second time we add a stroke to complete a x. At the end of the sequence, if we disregard all the x 's, we shall be left only with the initial T or B, or with the T or B followed by a /. If the T (or B) stands alone, the result of the computation will be read on the T (or B) side of the stock, but if a / follows, the result must be taken from the opposite side of the stock.
Problem 42. Find the value of (438 x 828 x 284 x 332 x 719)/(232 x 192x 505 x 266)
(i) Start with the first factor in the numerator then divide by the first factor in the denominator, next multiply by the second factor in the numerator and proceed in this manner until all factors have been used.
(ii) Write down and reduce the T and B symbols. Repeat taking the factors in different orders to see if the rules for finding in which scale d or D the result must be read give consistent results.
(iii) Also work through the problem by first multiplying together the factors of the numerator and then divide by the factors of the denominator, taking them in the order in which they are printed. Write down the T and B symbols, reduce them, and compare with the answer given at the end of the book.
We hope the reader has persevered in this matter of using the long scale of the Precision rule. We are confident he will not regret the time he has spent, and we recommend him to purchase a Precision rule should he not already possess one and if his work is of such a nature that it will benefit by a higher degree of accuracy. We know one man who uses a 10/20 rule for all his ordinary calculations, and, although we do not think it desirable to advocate such a practice, we should be sorry to be deprived of its use when it is applicable; we definitely prefer it to the rather clumsy 20" model we occasionally use.
Squares and square roots are obtained easily by projecting from the d or D scales, to the scales lying along the outer edges of the stock, and vice versa. These operations are so simple that they require no explanation.
The Precision rule is not recommended as a "first" slide rule; it is intended for those who are conversant with the standard type rule, and whose work demands its use.
Further examples, designed to illustrate the advantages of the 10/20 Rule will be found in Section 11, which explains the operation of the Dualistic slide rule. This rule is equipped with 10/20 scales. They occupy different positions on the rule from those we have just been studying, but the principle of working is the same.
© Hodder Stoughton, reproduced with permission.