| Slide rules HOME page | INSTRUCTIONS | CONTENTS |
SECTION EIGHT
THE COMMERCIAL RULE
The Special Commercial Scales-Money Calculations - Discount Scale - The Monetary Rule - £.s.d. Scales - Invoicing calculations.
[Note: This rule was produced in the United Kingdom before the introduction of decimal currency. At that the time the basic unit of currency was the pound sterling which was divided in 20 shillings each of which was further divided into 12 pence (the phrase "12 pennies" was normally written as "12 pence"). The penny itself could be divided into a quarter (a farthing) or a half (a half penny normally written ha'penny). The symbol for the pound was "£", for the shilling was "s." and for the penny was "d.". (The letters came from the Latin currency of Libra, Solidus and Denarius.)
A sum of 2 pounds, 12 shillings and 3½ pennies would be written £2, 12s. 3½d. This was equivalent to £2.614. Amounts of less than a pound might be written as 17s. 6d. or 17/6,]
We have expressed the opinion that to most people the slide rule is not the vade-mecum
it should be. The engineer, the architect, the draughtsman and many others would, at
times, find his work irksome and tedious without the aid of his slide rule, which helps
him to cope with a mass of detailed calculations.
Unfortunately, there is a deep-rooted impression that the slide rule is of little use for
commercial calculations, and especially for those which involve monetary values. It is
true that if a result is required correct to the last penny, the slide rule may fail to
give it, but there are many commercial calculations in connection with which the slide
rule will give valuable assistance. When the slide rule will not give results with the
necessary precision, it can always be used as a check, and in this service alone it is
worth a place on the desk. Should this section meet the eye of any individual who, whilst
dealing with accounts, does not use a slide rule, we ask him to keep an open mind on the
subject and to spend a few minutes in investigating the possibilities.
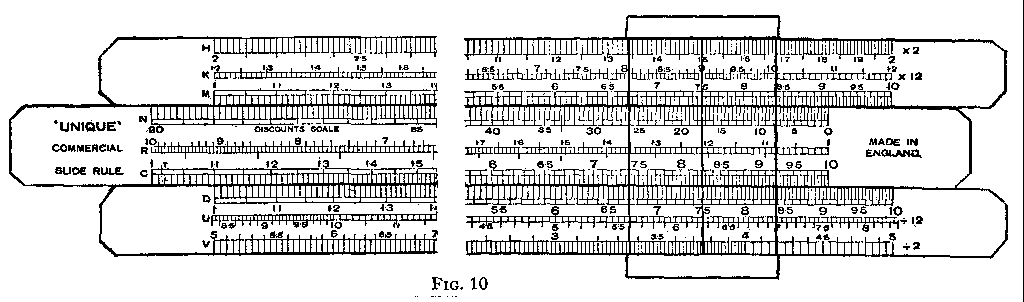
In Fig. 10 we illustrate a slide rule designed to meet the requirements of the commercial user. It will at once be seen that C and D scales, which we have studied earlier, and which we regard as being the most important scales in any slide rule, occupy their usual positions, C lying along the lower edge of the slide, and D on the stock adjacent to it. The M scale just above the slide is identical with D, but is used in conjunction with scale N.This combination of scales allows us quickly to calculate net amounts, after taking off discounts.

The scales H, K, U and V are all graduated in the same manner as C and D, but they are so placed that results appearing in D are automatically multiplied or divided by 12 or 20, when read directly above or below in H, K, U or V. Other ratios may be obtained by projecting directly from one scale to another, e.g. readings in K are 144 times those in U and 6 times those in H. Readings in H are 4 times those in V and 24 times those in U. Now all the numbers mentioned appear frequently in our calculations. There are 12 in a dozen, 12 pence in a shilling, 12 months in a year, 12 inches in a foot, 144 in a gross, 60 minutes in an hour, 20 shillings in a pound, 20 cwt. in a ton, 24 hours in a day. Many simple calculations can be made therefore by the simple process of projecting from one scale to another.
For easy reference we now show the relationships between the various scales in tabulated form.
Scale H. This scale is positioned, relative to other scales, so that any value in scale M or scale D is multiplied by 2 by projecting, by means of the cursor index X, from M or D into H.
These relationships are more easily indicated in the abbreviated form which we now employ:
| Scale H. | H=2 x M |
| H=2 x D | |
6 x |
H=K |
| H = 24 x U | |
| H= 4 x V | |
| Scale K. | K=l2 x M |
| K=l2 x D | |
| K = 144 x U | |
| K=24 x V | |
| scale M. | M=D |
| Scale N | This is a special scale which enables discounts to be quickly deducted. Scale M is adjacent to scale N for convenience in such calculations. |
| Scale R. | The reciprocal scale lying along the centre of the slide. We do not regard this scale as an important part of the scale equipment of a slide rule, but we know that some people consider its inclusion an asset. Its uses and limitations are discussed in Section 10 dealing with the Electrical rule. |
| Scales C and D | The scales we have studied in Section 4. |
| Scale U. | l2 x U=D=M |
| 144 U = K | |
| 24 U = H | |
| 6U = V | |
| Scale V. | V=6U |
| 4x | V=H |
| 24x | V=K |
We have purposely stated the ratios in terms of multiplication. The reader will readily appreciate that we could just as easily have stated them in terms of division. There is no necessity to memorise these scale relationships. It is sufficient to remember that 12, 2, 6 and 144 appear among them. With a little practice one soon becomes familiar with the most useful combinations.
Example: A certain type of coiled spring requires 8.25 inches of wire to make it.
What length of wire will be required to manufacture 50 springs?
Over 825D set 10C.
Move X to 5C.
Under X read 4125 in D or 344 in U.
Also 4U is opposite 48D.
The answer may therefore be read as
412.5 inches, or
34.4 feet, or
34 feet 48 inches.
Problem 35. The cost of 1000 articles in U.S.A. is 48 dollars. Find the cost of one gross in G.B. (rate of exchange $2.8 = £l). Use scales U, C and K.
Example: Convert 655 kilos into tons (454 grammes =1 lb.).
Over 655D set 224C.
Move X to lC.
Set 454C to X.
Read 645D under 10C.
Result: .645 tons.
Alternatively
Over 655D set gauge point T (1014) in scale C.
Read 645D under IC.
(This method makes use of the special gauge point marked T in scale C. 1016 kilos = 1
ton.)
Example: Below is part of a workman's time-sheet. His rate of pay for a 44-hour week is £7, 1s. 0d. For costing purposes, each job has to be charged with the labour cost.
| Job No. 904 | 8¼ hours |
| 918 | 2¼ hours |
| 721 | 45 mins. |
| 800 | 3¾ hours |
| 856 | 50 mins. |
Over 141D (141 = rate in shillings) set 44C.
Under 85C read 272s. in D or 327d. in K.
Over 45C read 29d. in H.
Under 375C read 12s. in D or 144d. in K.
Over 50c read 32d. in H.
For the second Job No. 918, the slide must be traversed, so
Move X to 10C.
Move 1C to X.
Under 225C read in D 72s. or in K 86½d.
The last example shows how more accurate results may sometimes be obtained by reading values in different scales. In the Job No. 918 the answer may be obtained in shillings If scale D and appears to be 72s. with a possible error of + 1d. in the answer is read in scale K we obtain 86½d. without any doubt as to the last penny.
In Job N0s. 721 and 856 the answers are read off in pence in scale H and the reader may perhaps have some difficulty in seeing why we change to this scale.
Consider Job No. 721. The computation expressed fully is 141/44. This gives the man's rate per hour in shillings; (141/41)(45/60) gives the man's rate for the job in shillings; and (141/41)(45/60)12 is the cost of this job in pence.
Now the 12 divided into 60 leaves 5 in the denominator and dividing by 5 is equivalent
to multiplying by 2, and this gives the reason for reading the result in scale ii.
For practice in this important type of calculation we ask the reader carefully to work
through the following problems.
Problem 36. A woman's rate for 42 hours is £4, 11s. 6d. Calculate the
labour costs to the nearest penny to be set against the following jobs.
| Job No. 121 | 3 hours |
| 129 | 4¼ hours |
| 167 | 6¼ hours |
| 188 | 35 mins. |
| 196 | 22 hours |
| 219 | 55 mins. |
Example: Goods bought at 22% below list prices are to be sold at 15%
above list prices. Calculate the selling prices corresponding to list prices of 8s. 6d.,
9s. 4d., 15s., 17s. 6d and 22s. 3d.
Now 100 - 22= 78
and 100 + 15 = 115
these calculations involve multiplying the original list prices by 115/78.
Over 115D set 78C.
Under 85C read 12s. 6d. in D or 150d. in K.
Under 933C read 13s. 9d. in D or 165d. in K.
Now traverse the slide, i.e.
set X to 10C and move slide to bring lC under X.
Under 15C read 22s. 2d. in D or 266d. in K.
Under 175C read 25s. 9d. in D or 309d. in K.
Under 2225C read 32s. 9d. in D or 393d. in K.
Problem 37. A man's rate of pay for 40 hours is £8, l0s. 0d. Calculate his rate per hour and the pay for 6½, 29 and 60 hours.
Example: A Hydraulic Power Co. charges 2s. l1d, per 1000 gallons of
water at a pressure of 950 lb. per square inch. Calculate the cost per horse-power hour.
(1 gallon water = 10 lb., 1 cu. ft. water = 62.3 lb.,1 h.p. = 33,000 ft.-lb./min.) The
relevant figures are:
35d. x (33000 x 60 x 62·3)/(10000 x 950 x 144)
which cancels down to
(33 x 62.3 x 35)/(950 x 24)
Over 33D set 95C.
Move X to 623C.
Set 24C to X.
Under 35C read 315D.
Answer: 3.15d.
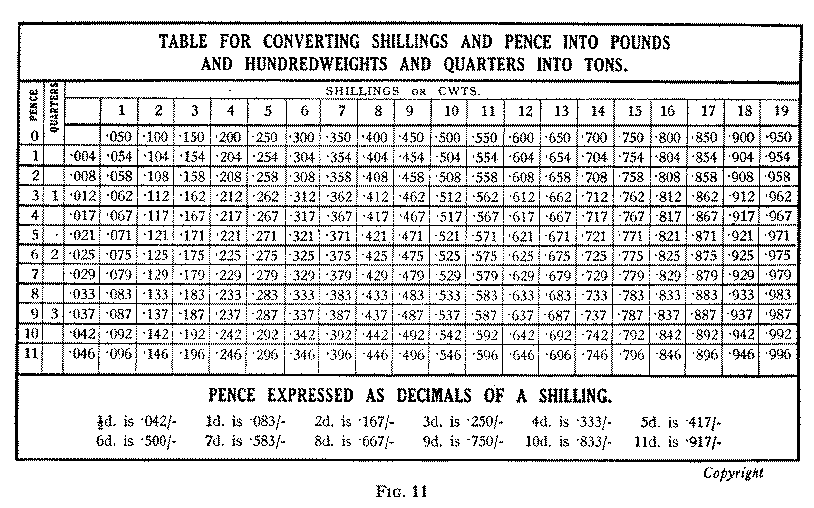
On the back of the rule a conversion table for decimalising is given; it is the equivalent of the table Fig. 11.
The reader is advised carefully to study the examples which now follow and to work out
the problems. Other examples are given in Section 16.
Example: An invoice price of £43, 16s. 6d. is subject to 33 1/3%
less 15% less 2½% What is the net amount?
From the table on the back of the rule or from Fig. 11 read 16s. 6d. = £ .825.
Set 0 of scale N to 43·825M.
X to 333N. (Note special gauge point at 331/3%.)
0 of N to X. X to 15M. 0 of N to X.
Above 2.5N read in M 24.2 = £24, 4s.
(The reader will please note that scale N reads backwards from right to left.)
We would here point out that we cannot add percentage amounts on by just reversing the operation defined above. The reader will easily see why this cannot be done: 50% off 40 leaves 20. If we add 50% to 20 we obtain 30, not 40. However, if we wish to add on percentage amounts we can do so easily by using scale C. Increasing a quantity by, say, 10% is equivalent to multiplying by 11. Calling the 1 of C a 100, and the 11 of C 110, we see that the space between 1 and 1.1 represents an increase of 10%. The 1.1 graduation, which we will call 110, is our 10% increase mark, the 1·3, called 130, is the 30% increase mark, and so on. If we use the graduation 2, which we must now call 200, we shall be adding 100%, and if we use graduation 3, we shall be adding 200%, and likewise. It will seldom be necessary to go to these high percentages.
Example: To 35 add 10%, then add 60%. (Please note that this is not
the same as adding 70% to 35.)
Set X to 35M. lC to X. X to 1·1C.
lC to X. X to 1.6C.
Read the result in M under X = 61.6.
Problem 38. Calculate £8, 4s. 2d. + 15% - 30% - 12½% - 7½% - 12½% + l0%.
Example: Calculate 17% of £108, l0s. 0d.
Please note that this is a different type of calculation from those immediately above. We
now use scales C and D.
Over 1085D set lC.
Under 17C read the result, 1842, in D.
Now we can see that 17% is approximately one-sixth, and our result must be £18.42 = £18, 8s. 5d. (Scale on back of rule shows £·42 = 8s. 5d.)
If you will work out this result precisely, you will find that to the nearest penny the correct answer is £18, 8s. l1d., and our slide rule has given us a result in error to the extent of 6d. 6d. in £18, 0s. 0d. is about 1 in 720, or less than one-seventh of 1%, and it is the sort of error we must expect with a 10" slide rule. We can do better than this, and we hope the reader will note how to make the best use of his slide rule.
17% of £100 is £17, 0s. 0d., and we can write this down without using a slide rule.
We now find 17% of the remaining £8, l0s. 0d.
Set l0C to 85D. Under 17C read £1·445.
Taking the nearest figure from the table we see that .446 = 8s. 11d, and our result now appears as
| £17 0 0 |
| 1 8 11 |
| £18 8 11 |
By breaking up the original figures into a large part which we can deal with mentally, leaving a smaller odd amount for slide rule calculation, we generally can get very near the exact result as we have done in this example. If the reader will work through the above, he will obtain the same result and satisfy himself that it is genuine.
Instead of using the table for converting £.445 to shillings and pence the reader may
prefer to use the H and K scales.
Set X to 445D. Read in H under X 89s.
Set X to 9D. Read in K under X 108d.
Thus £.445 is equal to 8s. l1d, to the nearest penny.
Problem 39. What is 22½% of £1662, 11s. 7d.?
(Work mentally 22½% of £1000, and of £600, and use the slide rule for the odd amount, then obtain a check by using the slide rule to take 22½% of £1663. This will give the result to the nearest pound.)
Example: In a factory time-sheet the following hours of overtime appeared:
| Mrs. A | 3½ hours |
| " B | 4½ " |
| Miss C | 4¼ " |
| " D | 2¾ " |
| " E | 7¼ " |
All these women are paid 78s. 0d. for 44 hours, and are paid 1½ times day rate for all
overtime. The amount of pay due to each is required. We shall calculate payments for
overtime and add them to the 78s. 0d. since more accurate results will be obtained.
To 78D set 10C. X to 1·5C. 44C to X.
Set X to 45C.
Under X read 11s. l1d, in D or 143d. in K.
Set X to 475 C.
Under X read 12s. 8d. in D. or 152d. in K.
Set X to 725C.
Under X read 19s. 4d. in D or 232d. in K.
Now traverse the slide to compute the overtime for Mrs. A and Miss E.
Move X to 10C. Set 1C to X.
Set X to 35C.
Under X read 9s. 4d. in D or 112d. in K.
Set X to 275C.
Under X read 7s. 4d. in D. or 88d. in K.
The overtime payments are Mrs. A 9s. 4d., Mrs. B 11s. l1d., Miss C 12s. 8d., Miss D 7s. 4d. and Miss E 19s. 4d. These amounts added to 78s. give the amounts to be credited to the various workers. This example shows that for small amounts of a few shillings the results may be read in scale K to the nearest penny.
This example shows how quickly pay for different hours worked can be calculated. There are alternative methods of working as the reader will realise, but all the workers on any rate, in the above 78s. 0d. should be dealt with together, since all the payments can be obtained at one or two settings of the slide. When the 78s. 0d. group has been exhausted, re-set the slide to, say, 82s. 0d. The slide rule will generally give results quite accurate enough for the purpose. When the method of working is appreciated, the slide rule will be preferred to the ready reckoner.
Problem 40. Calculate the simple interest on £59, 8s. 2d. for 182 days at 4¾% per annum.
Example: Convert $341 to sterling. Rate of exchange £1 = 2·86$.
Over 341D set 286C.
Under 1C read £119.2 = £119, 4s. 0d. in D.
Problem 41. A workman receives 8¾d. per piece. In the course of a day of 8½ hours he turns out 61 pieces. Calculate his earnings per day and per hour.
A great variety of examples could be given, but this book must be kept to moderate dimensions. Any calculation which involves the operations of multiplication and division may be effected by slide rule, and the reader will have no difficulty in finding opportunities for exploiting it. Further examples will also be found in Section 16.
The idea of constructing a scale in terms of pounds, shillings and pence will, by this time, have occurred to those readers who have persevered in the perusal of this book, more particularly to those who have studied the instructions immediately above concerning the Commercial rule.
The illustration of the Monetary slide rule, Fig. 12, shows such a scale.
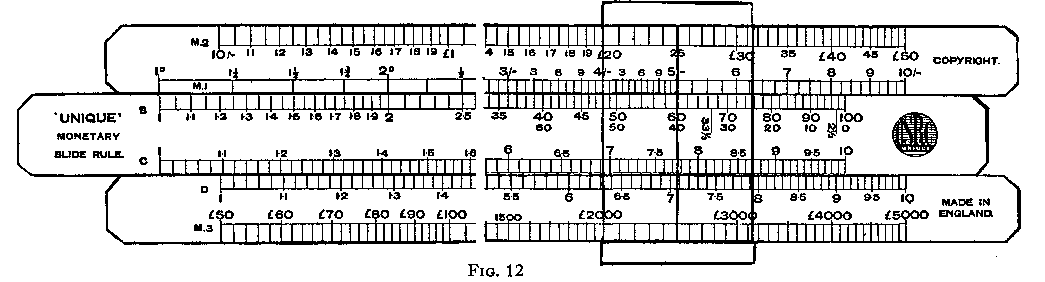
The monetary scale, lying on the stock of the rule, is in three sections designated by M1, M2 and M3. M1 lies immediately above the slide, and M2 and M2 along the top and bottom edges respectively. M1 commences at 1d. and in logarithmic intervals increases to l0s. at the right-hand extremity. l0s. is the starting value in M2 and this section of the scale extends to £50. M3 begins at £50 and proceeds to the maximum value of £5000. The complete scale, therefore, covers a range of 1d. to £5000.
(The reader will understand that the illustrations of the different slide rules are reduced in size and that a part has been omitted from each, further to reduce the lengths, so that the diagrams can be printed within the limits of the pages.)
The remaining scales in this rule are the B, C and D scales with which we are now familiar. In all the scales "legible" dividing has been adopted (legible dividing means that the spaces along the scales are wider and there are less graduations. If the reader will compare Figs. 10 and 12, the wider dividing in the latter will be apparent.)
The C and D scales have no connection with M1, M2 and M3. C and D are included so that this rule may be used for ordinary numerical calculations. They have been dealt with adequately in Section 4 and we shall make no further reference to them here.
Scale B is used in conjunction with M1, M2 and M3 for multiplication, division and discounts off.
First examine the three sections of this monetary scale. Place the cursor index X over the 1s. graduations in M1. Immediately above in M2 will be seen £5 and below in M3 £500. Thus values in M2 are 100 times those in M1, values in M3 are 100 times those in M2.
These relationships apply throughout the three sections of the M scale.
Now set the slide so that 1B is coincident with 4d. in M1.
| In line with | 2B | will be found | 0s. 8d. | in M1 |
| " | 3B | " | 1s. 0d. | " |
| " | 10B | " | 3s. 4d. | " |
| " | 30B | " | l0s. 0d. | " |
In effect, with this setting of the slide the 4d. selected for illustration, is multiplied by any selected number in scale B by reading the results in M1. Division is effected in the reverse manner. The rule setting we have adopted will effect division of l0s. 0d. by 30, 6s. 0d. by 18 and many other examples. Now traverse the slide, i.e. push it to the left and set it so that 100B is brought into coincidence with 4d. in M1. Set X to 60B and read in M2 the result of multiplying 4d. by 60, viz. £1. In the first setting of the slide, some of the numbers in B were off the M1 scale. It is, we think, obvious that these missing values would have given results in M2 if M2 had formed a continuation of M1, but since M2 has, in effect, been moved to the left a distance equal to the length of the scales, the slide must be moved similarly. This complication need not give any concern since it is only necessary to remember "If when multiplying, the 100 of scale B is used in setting the slide, the result will be found in the next higher M section." The corresponding rule for division is fairly obvious, and we leave it to the reader to put into words.
When we examined the A and B scales in Section 5 we saw that in multiplication or division if we desired to use say 25 in some computation, we could select the 25 in the left-hand half or the 25 in the right-hand half of the scale without affecting the final result. It must be remembered when using this Monetary rule, that we must use the appropriate figure in scale B. Reverting to the earlier setting of the slide with 1B set to 4d. in M1, we find opposite 25B the result l0d. and opposite 25B the result 8s. 4d. Both results are correct, but we shall be in error if we use 25 when 25 is called for.
It will be sufficient now if we give a few examples illustrating the uses to which this ingenious rule may be put.
Example: Calculate the invoice value of 72 pieces at 3s. 9d. each.
Set 100B to 3s. 9d. M1.
X to 72B.
Result in M2 under X is £13, l0s. 0d.
If this amount is subject to less 40% less 10% and less 4% find the nett amount by
setting 100B to X.
X to 40%. 100B to X. X to 10%. 100B to X. X to 4%.
Result: £7, 2s. 0d. in M2 under X.
Example: Multiply 1s. 4d. by 5·8, 580 and by 58,000. Set 1B to 1s.
4d. M1. X to 5·8B.
Under X read 7s. 9d. in M1, £38, l5s. 0d. in M2 and £3,875 in M3.
The reader will appreciate that towards the end of the M scale, values cannot be determined with accuracy. This end of the scale will seldom be used in normal calculations but will always provide a check.
Example: The pay rate for a certain operation is 1s. 9d. per piece. Calculate the
pay due for 3½, l8½, 22, 39 and 42 pieces.
Set lB to 1s. 9d. in M2.
Against 3½ B read 6s. 2d. M1.
Set 100B to 1s. 9d· in M2.
| Xto l8½B; | amount in M2 under X is | £1, 12s. 5d. |
| 22 B; | " | £l, 15s. 6d. |
| 39 B; | " | £3, 8s. 3d. |
| 42 B; | " | £3, 13s. 6d. |
We can think of no more valuable aid for the costing, in voicing and purchasing staff in a busy office than this slide rule. For many purposes results obtained with it will be sufficiently accurate, and in those calculations where the "last penny" must be correct the rule is a great aid in checking.
In weekly wages calculations, where the amounts are of the order of a few pounds, the rule will give reliable results.
© Hodder Stoughton, reproduced with permission.