Trigonometric calculations (sine and tangent)

Differential trig scales

Introduction

It is not the purpose of this site to teach trigonometry, rather how to use trig scales on slide rules. For this purpose we will look at typical examples using trig scales in different positions on the rule.  This page is related to rules with the differential trig scales patented by the British company Thornton and only found on their rules.

As an example we use a P.I.C 131. This 10" rule has the usual arrangement of these scales with the Inverse trig functions on the slide to the left and the trig functions on the slide to the right. For a general description of this rule see the  Thornton 131.

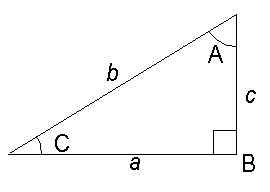
Right angle triangles

Example 1
To find the length of c given the length of a (3.9) and angle C (31°).

The formula is:    c = a tan C

Method
    Cursor to 31 on D.
    T 31.0° to cursor.
    Answer (2.34) on D against 3.9 on C.

Example 2
To find the angle C given the length of a (4.5) and b (7.9)

The formula is: C = sin^-1 (a/b)

Method
    Align 7.9 on C with 4.5 on D
    Cursor to 10 in C (=0.57 on D)
    Align 0.57 on inverse sine to cursor
    Answer 34.4° against 1 on D scale.

Front view

Back view

Example 3

To find the length c given the angle C (27.0°) and the length b (8.2)

The formula is:
    c = b sin C

Method
    Cursor to 27 on D
    27.0° on S to cursor
    Cursor to 8.2 on C
    Answer (3.72) under cursor on D.

Scalene triangles

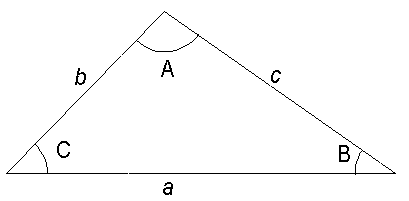
Example 4
To find c given b (2.3) , C (47.0°) and B (32.0°)

The formula is:
    c = b sin C / sin B

Method
    Cursor to 4.7 on D
    2.3 on C to Cursor
    Cursor to 32° on S
    47° on S to cursor
    Answer (3.17) under 2.3 on D.

Step 1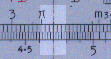

Step 2

Step 3

Step 4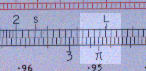

Tan and sin of small angles (<5.7°)

Up to now, for angles greater than 10° we have used the value on the D scale times10 to align against the appropriate angle on the S or T scale. For small angles, 1° to 10°, use the value as written on the D scale. For smaller angles use 0.2 times the D scale value and so on.

Tan of large angles ( > 60.0°)

For large angles use the value of tan 90° minus the angle and read the answer on the C scale against the 1  on the D scale.

The example shows tan 75.
    90 - 60 = 15
    15 on the D scale is aligned with 15° on the tan scale.
    The answer 3.73 is on the C scale against 1 of the D scale.