Trigonometric calculations (sine and tangent)

Trig scales on stock (stator)

Introduction

It is not the purpose of this site to teach trigonometry, rather how to use trig scales on slide rules. For this purpose we will look at typical examples using trig scales in different positions on the rule.  This page is related to rules with the trig scales on the stock.

As an example we use a Faber Castell 62/83N. This 5" rule has four trig scales, two for tan (T : 5.6° to 45° and 45° to 84.6°), one for sin (S : 5.6° to 90°) and one for sin and tan for small angles (ST : 0.56° to 5.6°). Relatively few rules have the second tan scale and some do not have the ST scale. We discuss below how to calculate the tan of angles outside the range of the scales. The advantage of a 5" rule is that distances are smaller which makes for more compact diagrams.

This rule has the angles graduated in degrees and decimal fractions of a degree. Other rules may have the angles graduated in degrees and minutes or in grads.

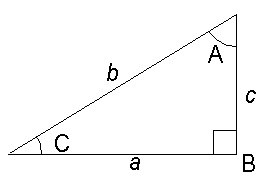
Right angle triangles

Example 1
To find the length of c given the length of a (8.0) and angle C (30°).

The formula is:    c = a tan C

Method
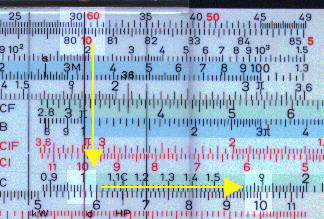
     Cursor to 30.0 on T
    10 on C to cursor
    Answer (4.62) on D under 8.0 on C.

Example 2
To find the angle C given the length of a (4.5) and b (8.0)

The formula is: C = sin^-1 (a/b)

Method
    8.0 on C to 4.5 on D.
    Cursor to 10 on C.
    Answer 34.2° under cursor on S.

Example 3

To find the length c given the angle C (27.0°) and the length b (1.3).

The formula is:
    c = b sin C

Method
    Cursor to 27.0 on S
    1 on C to cursor
    Answer (0.59) on D under 1.3 on C

Scalene triangles

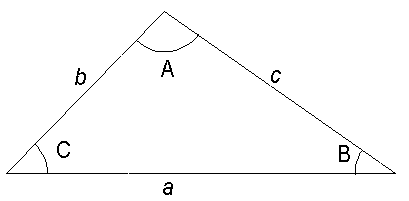
Example 4
To find c given b (2.3) , C (50.0°) and B (32.0°)

The formula is:
    c = b sin C / sin B

Method
    Cursor to  32.0 on S
    2.3 on C to cursor
    Cursor to 50.0 on S
    Answer (3.325) under cursor on C.

Tan and sin of small angles (<5.7°)

For small angles tan and sin are almost equal. To calculate the sin or tan of a small angle multiply the angle by 0.01745. Some rules have a gauge point at this value.

Tan of large angles ( > 45.0°)

For slide rules without a second tan scale align 90 minus the angle with 1 on the C scale, the answer is on the C scale under 10 of the C scale. (Note although this rule has two tan scales, for consistency this rule is used for the explanation).

The example shows tan 60.
    90 - 60 = 30
    30 on the tan scale is aligned with 1 on the C scale.
    The answer 1.73 is on the C scale against 10 of the D scale.