Timber rules

Introduction

It is difficult for us now to imagine how important timber was before the widespread use of iron, steel and concrete. Even if built of brick all the internal construction of a house was wood: coaches and wagons for transport of people and goods were made of wood: ships were also built of wood. A good carpenter who knew his craft and how to perform the calculations appertaining to it was a prized member of society.

Timber rules

Timber rules, of course, existed before slide rules. One was found on the Mary Rose, a ship which sank in 1545. This rule, like other early rules, also had a scale to enable the cubic content of cut timber to be estimated without need for pen-and-paper calculation. As far as slide rules for timber calculations are concerned the critical date is 1677 when Henry Coggeshall produced the first edition of a booklet entitled "Timber Measure by a line of more Ease, Dispatch and Exactness, than any other Way now in Use By a DOUBLE-SCALE." The rule he described had two logarithmic scales, one of which had a single cycle and ran from 4 to 40 and a second of the same length had two cycles and ran from 1 to 100.  In later editions a rule with two more scales is described and this became for more than 200 hundred years the standard format of such rules. There was a fixed 'A' scale of two cycles of logarithms from 1 to 100, a slide with two scales, 'B' and 'C', also of two cycles of logarithms from 1 to 100 and a fixed 'D' scale of 1 cycle of logarithms from 4 to 40. This line, 'D', is usually called the girt line. So if you have this combination of scales and the words "girt line" then you almost certainly have a timber rule.

Other slide rules had of course existed earlier and may have been used for timber calculation. Coggeshall refers to a rule by Partridge which he dismisses as being too complicated. Samuel Pepys, the diarist, on 15 April 1662, wrote about "reading of my book of Timber measure, comparing it with my new Sliding Rule brought home this morning with great pleasure.". This may have been an immediate precursor of the Coggeshall rule.

(Note: These instruction assume that you are familiar with slide rules and the fact that a given number may represent a number 10, 100, 1000 etc times larger or smaller)

To multiply two numbers

 Set 1 (or 10) on B to the multiplier on A, and against the multiplicand on B the answer will be found on A. Example, to multiply 16 by 23. Set 10 on B to 2.3 on A and against 16 on B the answer 368 (3.68) is on A.

(Note: I am using a 2 foot timber rule rather than the more common 2-foot 2-fold rule as on this rule the numbers are clearer.)

To divide one number by another

Set the divisor on B against the dividend on A, the required quotient will be on A against the 1 or 10. For example to divide 24 by 8. Set 8 on B against 24 on A. The answer, 3, is on A against 10 on B.

To find the geometric mean of two numbers

This is not just an academic exercise - for carpenters this is very important. If a piece of timber is of rectangular section then its volume is length times the geometric mean of the two sides. Using C and D scales set one of the numbers on C to the same number on D. The geometric mean is found on D against the second number on C. For example to get the geometric mean of 7 and 15. Set 15 on C against 15 on D. Against 7 on C read 10 ¹/₄ on D. (Note. Many timber rules used fractions of an inch for some scale rather than decimals.)

To find the volume of squared timber.

Set the length on C against 12 on D and against the width on D will be found the volume on C. For example if a piece of wood is 10" by 10" and 8' long, set 8 on C against 12 on D and against 10 on C is found the volume 5.58 cubic feet.

To find the volume of rectangular timber.

From the early 19th century a new type of timber rule was introduced which did not follow Coggeshal's pattern. This was a double sided rule and on the reverse face to the traditional scales were 4 more scales. One called an 'inverted line' and labelled E which had two logarithmic cycles on the body of the rule, two scales labelled C and B on the slide and and one scale labelled A on the rule. The scales A, B and C also had two cycles of logarithms. The scale on the inverted line ran in the opposite direction to the other scales and was so arranged that the A scale was equal to the values on the E scale (inverted) divided by 144.   

To use this rule to calculate the volume of piece of timber of rectangular section, set one side in inches on E and the other side in inches on C. The volume in cubic feet is found on B against the length in feet on A. For example if a piece of timber is 7" by 15" and 24 ft long. Set 7 on the E (upper) scale against 15 on the C scale. The volume, 17.5 cubic feet, is found against 24 on the A, bottom scale.

For a more normal Coggeshal type rule there were two options:

1. Calculate the geometric mean of the two sides as described above.
2. For some reason the more common method seems to have been to have have taken the quarter circumference, in effect the arithmetic mean of the lengths of the two sides. It recognised that this was in error. Some source simply record that fact and others gives tables of correction.

To find the volume of round timber

The normal method was first to measure the circumference and take one quarter of it. This could easily be done by passing a piece of string around the timber then folding it in two and then again in two and measuring its length. Set the length in feet on the C scale against 12 on the D scale and the volume will be found on the C scale against the "quarter girth" in inches, sometimes referred to simply as the "girt", on D. For example, if the wood is 10 feet long and10" quarter girth set 10 on C against 12 on D and against 10" on D in the answer 6.93 cubic feet on C.

The same calculation is shown below on a 2-foot 2-fold rule.

If you assume the tree is cylindrical and calculate the volume using a calculator you get the answer 8.84 cubic feet - so what has gone wrong. Well, the answer is nothing according to practice. Thom, in an 1846, book on mensuration states:

"When the square of the quarter girt  is multiplied by the length the product it gives a result nearly one fourth less than the true quantity in the tree. This rule, however, is invariably practised by timber merchants, and is not likely to be abolished."

This volume is equivalent to the enclosed square which could be cut out a round piece of timbers and is less the full amount by p /4. This leaves an allowance for waste when the tree is shaped. To get the full amount you place the length against 10.63 on the D scale and the rule above has a gauge point expressly for that.

Another alternative, due to Hutton, is to multiply the square of one fifth of the girt by twice the length. This gives a value very close to the true content. For example, using the values above, if the quarter girth is 10", then one fifth of the girt is 8 inches. The volume thus calculated is 8² times 10 x 2 divided by 144 to convert to cubic feet, 8.89 cubic feet. This is very close to the above value. (Effectively  this method assumes that p is 25/8, i.e. 3.125 rather than 3.1415, an error of 0.5%.)

This method was not as easy to apply as the quarter girth method. It is easy to fold a piece of string twice to get a quarter but not as easy to fold it to get 1/5. To overcome this special measuring tapes were sold with both 4" and 5" graduations.

Polygonal sections

Side and Edge scales

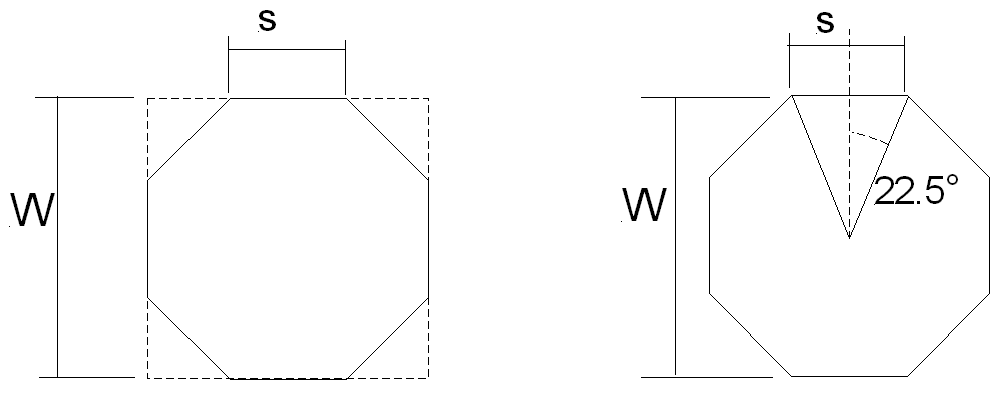
A very common task of a carpenter was to convert a piece of wood to a polygonal cross-section  as a first step to producing a circular cross-section for ships mast. However going from a square section to an octagon implied a non-trivial arithmetic task. The diagram below show two possible ways of calculating where to cut the square section. In both cases the width of the square section is W and the required side of the octagon is s.

On the left hand side of the diagram the width, W, can be expressed as:

W = s + 2 (s / Ö 2)
W = s (1+Ö 2)
and
s = W /(1+Ö 2)

To mark out the position of the cut line, knowing the length of the side does help much, what is needed is the distance from the edge or the middle of the square face. The distance from the edge (E) to the cut is:
E =s/Ö 2
as s = W /(1+Ö 2)
we can write
E = W /(Ö 2(1+Ö 2) ) = W(2+Ö 2) =  W /3.414

The distance from the middle, M, is:
M = s/2
as s = W/(1+Ö 2) 
we can write
M = W/(2(1+Ö 2)  ) = W / 4.828

This gives us the ratio to be applied to width of a square piece of wood to cut an octagonal piece of wood.

To facilitate this calculation some rules have lines marked E and M. An example from a rule by Buck and Hickman dated to around 1840 is given below. This shows that if the width of the square piece of wood is 34", the cut line for an octagon can be marked about 9 ⁷/₈"  from the edge or 7 ¹/₈" from the middle. The same scales are sometimes named "Square" and "Line".

Polygonal gauge marks

The timber rule used for many of the above diagrams has gauge marks for girt line and diameter of circular, 8 sided and 16 sided timber. They effectively mark the quarter girth (girt) or diameter of a circle or polygon whose sectional area is 144 square inches.

For the diameter the maths is relatively easy:

Sectional Area = 144 = p D² /4.
D = Ö  (4 x 144 /p ) = 13.54" (which corresponds to the mark on the rule)

For the quarter girth, G, the calculation is:

Sectional area = 144 = p D² /4, as above
G = p  D/4 and therefore D = 4 G /p 
Substituting gives:
144 = (p / 4) (4 G /p  )² = 4 G² / p 
and
G =Ö (p x 144 / 4) = 10.63" (which also corresponds to the mark on the rule)

For polygons the above diagram shows the case for an octagon. In the general case the angle q, shown above as 22.5° for an octagon, is 360°/(2N), where N is the number of sides. If we take R as the perpendicular distance from the centre to a side whose dimension is S, the area is N x S x R /2.  S is equal to 2R tan q, so R is equal to S /2(tan q) We therefore have, in a similar way to above:

Sectional area = 144 = N x S / ( tan q/2)/2   = N x S x S /4 tan q
and
S = Ö (576 tan q / N ) = Ö (576 tan (360/2N) / N )

For n = 8, S = 5.46
G = 8S/4 = 10.92"

For n=16, S = 2.66
G = 16S/4 = 10.70"

For a polygon let us define the diameter as 2R. (i.e. the distance between parallel faces). In this case, for the octagonal section R is equal to S/ 2 tan 22.5 so the diameter is 13.18". For the 16 sided section the diameter is 13.37".

All the values in bold face above correspond to the gauge marks on the rule.

Load tables

On some rules you find tables of the cost transporting a "load" of timber. A load was generally assumed to be 50 cubic feet. Hard woods generally weigh around 45 pounds/cubic foot so a load would weigh 2250 pounds, almost exactly  an English ton.

The above is part of a table. The price per load is given in the first column. The full numbers above the line are in pence and the intermediate values are farthings. For a description of pre-decimal currency in the United Kingdom see here (Opens new window).

If a load cost 13 1/4 d (13 pence and one farthing) per cubic foot, 50 cubic feet would cost 662 1/2d, or £2 15s 2 1/2d. Other rules use different combinations, some only use 40 cubic feet as a load and other have different rages of price per load.

Other rules have alternative forms of load scales. The one below is for planks 12" wide.

Consider the line marked 11 1/2". Against it is shown the length of 52' 2", i.e. 52.17'. Multiplying this length by 11 1/2" by 12" for the breadth and dividing by 144 to convert to cubic feet gives 50 cubic feet. i.e. a "load" as defined above.

This next one is for square scantlings.

In this case the table is of variable accuracy. The value for 12” square, given as 50 ft, for 10” square, given as 72 ft, and for 10 ½” square, given as 65’ 3 ½” are correct. For 11” square the table gives 60 ft but the actual value should be 59.5 ft, in other words 59’ 6’.

Scaling (proportioning scales)

Many timber rules had special scales for working from a scale diagram or for scaling a particular design up or down. As can be seen the main marks are divided in 12 (6 for the smallest scale)  and the range goes from ¹/₄ to 1 ¹/₂.  This enables a carpenter to take off scale measurements from a ship's engineer or architect from ¹/₄" to the foot up to 1 ¹/₂" to the foot.

The photo below shows an alternative arrangement of these scales. The ones shown are equivalent to ¹/₄" or ¹/₂" to the foot. This arrangement is simpler to mark to mark on the rule.  The arrow shows the distance for 5' 1¹/₂" at a scale of ¹/₄" to the foot.

The above scales are constructed on a similar principle to the Diagonal Scales described by Coggeshall. For a modern explanation see Sieber’s paper in the Journal of the Oughtred Society.

The Diagonal Scales and Proportioning Scales could co-exist. The following diagram, from a 6” rule (not a slide rule) shows the Diagonal Scales from one side of the rule and the scales from the other. In this case the diagonal scale is used as exactly as described by Sieber.

Acknowledgements

Bready J. and Babcock B., "Measuring the Volume of Logs: The Timber Contenting Slide Rule", Journal of the Oughtred Society Vol. 6, No 2, Fall 1997.

Nesbit A., “A Treatise on Practical Mensuration” ,1824.

Heather J. F., “A treatise on mathematical instruments”, 2nd edition, 1853.

Thom A., “A Treatise on Mensuration for the Use of Schools”, 1846.

Sieber J.L., “Calculating Using the Diagonal Scale”, Journal of the Oughtred Society; Vol.10. No 2, Fall 2001,

Hutton C., “Compendious measurer”, 7th edition, , 1812

Some of the images are of slide rules in the collection on Mick Taylor.

My thanks also to Peter Hopp for making valuable suggestions.