Before the invention of calculators, the only alternative to slide rules was to use tables of logarithms. These were published to varying degrees of accuracy.

The first example shows a page of logarithms to 4 figure accuracy and the second to 7 figure accuracy.

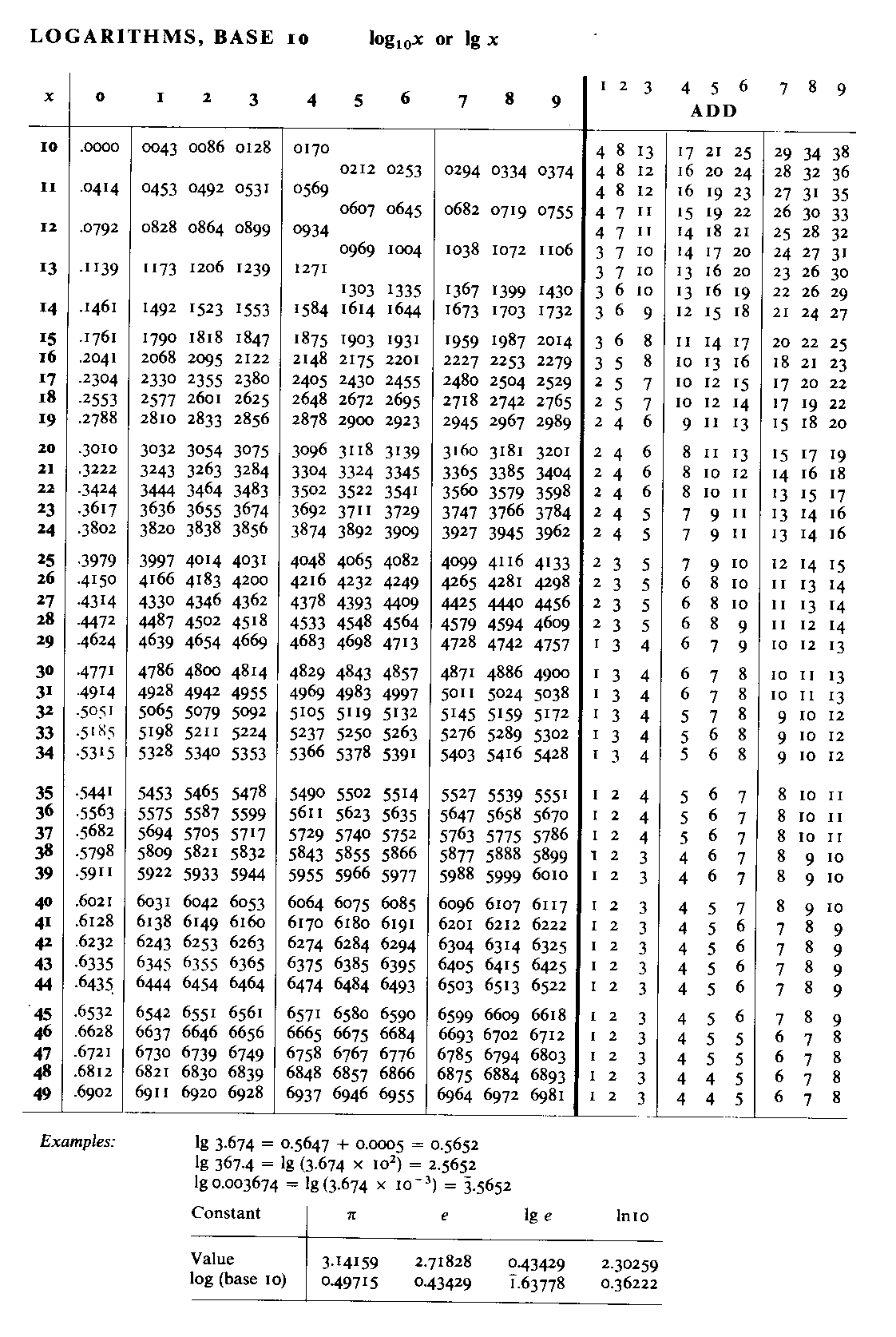
These were the most common form of logarithms and until the 1970s would have been familiar to most school children. The following is one page from a book of tables. With 4 figure logs the whole range of values could be covered in 2 pages. Other pages would have included anti-logarithms and trigonometrical functions. One thing which should be noticed, and which is particularly relevant in a slide rule site, is that fixing the decimal point had to be done in a similar way to that of slide rules. The example given below shows that log 3.674, log 367.4 and log .003674 are respectively 0.5652, 2.5652 and -3 + 0.5652.

Slide rules were almost as accurate as 4 figure logs and were a lot quicker in their use.

These were used where higher accuracy was needed and were much more cumbersome. For example in my book of 7 figures logarithms, the logarithms alone occupy 200 pages (compared to 2 pages above).

For other calculations, say involving trigonometrical functions, the logarithms of the functions were tabulated. This facilitated such calculations as 3.764 x sin 40° since one could go straight to log (3.764) + log (sin40°). The example below shows one page (of the 90) dealing with logarithms of sines, tangents, etc.

Note also the column of differences. If one wanted to calculate log (sin 13° 15' 35" ) then from the table this would be calculated as:
     9.3602154 + (35/60) * 5361
Presumably for convenience of presentation, the values are given for a base distance of 10,000,000,000 units.