Gauging

Introduction

Some 50 years after the invention of the slide rule there were two major developments. The first of these was the timber rule by Coggeshall in 1677 and the second the gauging rule by Everard in 1683. Everard was a Customs and Excise officer and therefore very much concerned with calculating the amount of duty to be paid on alcoholic drinks. His rule was described in a book entitled "Stereometry made easie, or, The description and use of a new gauging-rod or sliding-rule: by which the content of any tun, copper, cask, or other vessel may be readily found, either the whole or any part thereof, the area's of circles in gallons and casks being found by inspection only: also the extraction of the square and cube-root ... : to which is added an appendix containing the description and use of another new rule, very useful in gauging of worts, and resolving questions in the mensuration of solids and superficies." The main use of these rules was to calculate the content of barrels, given the curved form of the barrel staves, a non-trivial task particularly if the barrels were only partly full - which could be either be standing or lying. Although we think of tax as being applied to alcohol content it was also applied to malt used for making beer or whisky and to other things such as soap.

Everard's original slide rule consisted of a stock of square cross-section with slides on two opposing faces. For such a rule see here. Later developments produced slides on all four faces and a duplex (two faced) slide rule with two slides. The examples here are from three rules,  two of them made by made by Dring and Fage and the third by Barnett. The first Dring and Fage, with slides on four faces, was made between 1796 and 1804. The second is a rectilinear rule with two slides on each of two faces, what in modern parlance would be called a duplex rule. This rule is later, around 1868. The third rule, also 4-sided and similar to the first, was also made around 1800.

These dates are important, before 1824 and the introduction of imperial measures there were different gallons for ale, wine and corn. After that date there was a unified imperial gallon. Some key units are:

Wine gallon - 231 ins³ (This is also a US gallon)
Ale gallon - 282 ins³ 
Corn Gallon - 268.8 ins³
Imperial gallon 277.42 ins³
Bushel - 8 corn gallons 2150.42 ins³ , defined as a cylinder 18.5 ins diameter and 8 ins high. This and the corn gallon were used for dry measure.

Cylindrical casks (barrels)

Whilst most casks are not cylindrical, the calculations for other casks are based on this shape. The image below shows the rules set up for a cask which is 40" long and 27" diameter. For Wine Gallons set the length, 40", against the WG gauge point and against the diameter, 27", on the upper scale read the volume, 99.1 wine gallons on the C scale. You can check this out using the volume of cylinder and the volume of a Wine gallon as 231 ins³ .

Using the later rule and the same dimensions set the length, 40", against the ImG gauge point and against the diameter, 27", on the upper scale read the volume, 82.6 imperial gallons, on the slide.

It should be noted both rules have a single scale from 1 to 10 on the slide but a split scale from 1 to p on the upper stock and p  to 10 on the lower stock.

Dry measure

Both rules have a separate scale for measuring malt (In the brewing process grains of barley, rarely other grains, are soaked in water. After a few days they start to sprout. At this stage the grains are called malt. It is the sugar content of the malt which is turned into alcohol in the fermentation process.) The grains are laid on the floor in a slightly irregular way. It is normal to measure the width, length and depth in a number of places and take the average.

Suppose the length is 114 inches and the width 58.5 inches then set the length, 114 on the B scale, against the MB gauge point on the A scale. Against the width, 58.5 on the A scale,  read the number of bushels per inch depth, 3.10, on the B scale.

Using the same dimensions on the other rule and proceeding in the same fashion the same answer is obtained.

Curved casks

Casks were usually divided into 4 varieties depending the degree of curvature of the staves. The first variety is the middle frustum of a spheroid; the second, the middle frustum of a parabolic spindle; the third, two equal frustums of a paraboloid united at their bases; and the fourth, two equal conic frustums united at their bases.

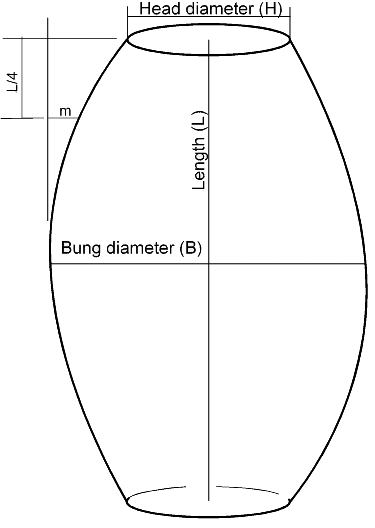
To determine the variety of the cask the following method was used:
    Measure the head diameter , H
    Measure the bung diameter , B
    Measure the length, L
    At a distance L/4 from the top measure the dimension marked m on the above diagram.

Then:
    If m = (B - H) /8 , the cask is a middle frustum of a parabolic spindle (second variety),
    If m < (B - H) /8 , the cask may be taken as spheroidal (first variety),
    If (B - H) /8 < m < (B - H) /4 , the cask may be taken as the middle frustum of a hyperbolic spindle (variety 3)
    If m = (B - H) /4  , the cask is formed of two equal conic frustums (variety 4).

The calculation of the volume of a curved cask is complicated and a number of formulae have been published for this taking account of the form of the cask. The method used by slide rules for this calculation is to estimate the diameter of the equivalent cylindrical cask and then to proceed as with the above calculation. The basic method is of the form:

Equivalent diameter =  Head diameter + a * (Bung diameter - Head diameter)

Where:
    Head diameter is the diameter at the "narrow" end
    Bung diameter is the diameter at the middle.
    a is constant and is a function of the shape of the barrel.

Both rules have scales for the calculation of the equivalent diameter. In the case of the older rule these scales are on the back of one of the other scales.

In the case of the later rule these scales are on the side of the rule. In this case the word Spheroid has been abbreviated to Sphd.

As can be seen against the 10" mark the value on the "spheroid" scale is 7.05 and on the "2nd variety" scale is 6.45.

To calculate the volume of cask with a length of 42", a bung diameter 33" and a head diameter of 27", use the 2nd variety scale to get the diameter of an equivalent circular cylinder. Bung diameter - Head diameter = 6. From the scale above the equivalent diameter is 3.79 + 27, i.e. 30.79.  The following image shows the rule set up with the length (42") against the WG gauge point and the volume ( 135 gallons) against the effective diameter (30.79"). Note that this calculation makes use of the fact that two of the slides can be used together.

Using the other rule for a barrel 48" high, 30" head diameter and 36" bung diameter. In this case the effective diameter is 30 + 3.79 = 33.79". Set the height 48" against the ImG gauge mark. Read the volume, 155 gallons, against the effective diameter 33.79.

Casks - partly full

The calculation of the volume of liquid in casks which are partly full is known as "ullaging". There are two options; the cask is standing or the cask is lying. In both cases the calculation is in two stages. First find the percentage of the full volume and secondly multiply the full volume by this percentage.

The first example in the image below is for a cask standing on end (S.S. = segment standing) with a height of 48" and a depth of liquid of 36". In this case the barrel is 77.2% full. The stock above the slide is a continuation of the stock below the slide for small depths. For example in this a depth of 3.5" would hold 5.95% of the full content.

The second example is the same as the above but using the later rule. As you can see this gives the same result. This rule also has a scale for small depths, in this image below the other scale. 

Other gauge points

The earlier rule has a several gauge points and divisors on the back of the slides.

As well as marks for ale, wine gallons etc there are also marks for:
MT - Malt tuns - in this case the bushel allows for settlement of the contents.
Malt - Malt bushel.
G St. - Green starch
D St. - Dry starch
HS Hot - Hard soap, hot
HS Cold - Hard soap, cold
G SS - Green soft soap
W SS - White soft soap
FG - Flint glass
PG - Plate glass
CG - Crown and broad glass
GB - Phial and bottle glass
LW - Low wine (the low strength first distillate before rectification to spirits, it typically has an alcohol content of 20%)
Do - Ditto
Verj - Verjuice (juice from up-ripened grapes, from the French "vertjus" i.e. Green juice)
Vin - Vinegar.
Sweets - Made wines using grape concentrate or added brandy and also mead, a wine a made from honey.
Mum - Wheat beer and other types of beer with beans and herbs.

For example the gauge points for Ale are 16.8S (for square) and 18.95C (for circular). One inch depth of Ale in a square container with the 16.8" side has a volume of 282.24 cubic inches; a circular container of 18.95" diameter has a volume of 282.08 cubic inches. In other words they represent the volume of an Ale gallon which is 282 cubic inches. The divisors for Ale are 282S and 359C and represent the square of the gauge points.

The next two images show conversion factors between different type of dutiable liquids. One is from the same Dring and Fage rule as the above and the other from a rule by Barnett of about the same date. The X refers to Strong Beer, the VI  to Small Beer and the C to Cyder.  Small Beer was beer made from products which had already been used to make strong beer. The imposition of excise duty had to be renewed every year by the annual Malt Act. The rates for cider in an act of around that time (quoted in William Symons "The Practical Gauger" of 1803) were:

• 4s0d per hogshead(63 wine galls),
• 6s11d made and sold in quantities of 20galls and upwards by any dealer or retailer, from fruit of his own growth, to be paid by such dealer or retailer,
• 7s8d if the same be received by any person to be resold by him, an additional duty to be paid by such person,
• 18s7d made and sold by retail, to be paid by the retailer (i.e. 4s0d + 6s11d + 7s8d).

These are the same rates, with the figure 's' for shillings and 'd' for pence, as shown on the second rule.

My thanks to Tom Martin who interpreted many of the marks on the rule and provided the corroborating evidence on the rate of duty.

My thanks also to Google books which provided some valuable reference material.