| HOME | INSTRUCTIONS | A-to-Z |
Gauge points
The are certain numbers which are used frequently in calculation; an obvious example is p (3.142). To save the user having to remember these values they are sometimes marked on the rule with a symbol to indicate their purpose. The following table gives some of the commonest gauge points, the normal and alternative designation and the value. The value is given twice, the "nominal value" is where you would find it on the rule and the "true value" is the value used for calculations.
| Normal Designation |
Alternative Designation |
Nominal Value |
True Value |
Uses |
| c | 1.13 | 1.128 | =Ö (4/p) - volume of a cylinder | |
| 1.146 | 1146 | (180 x 60)/(p x 3) the "Gunner's mark" (See below for more details.) |
||
| r" | s | 2.06 | 20655 | seconds per radian |
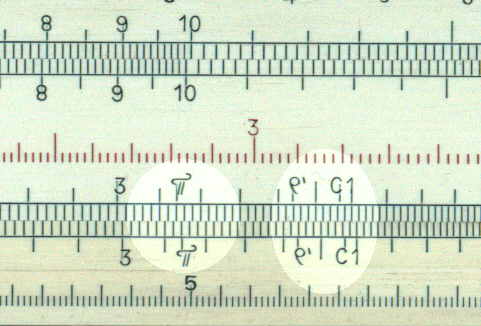
| p | 3.142 | 3.142 | ||
| r' | m | 3.44 | 3438 | minutes per radian |
| c1 | C | 3.57 | =Ö(40/p)- volume of a cylinder | |
| r11 | rg | 6.36 | Equivalent to r" for centesimal system. | |
| Q | V | 1.74 | 0.01745 | sin 1° = tan 1° |
| L | L,loge 10 | 2.30 | 2.3026 | loge 10 |
| p/4 | 7.85 | .785 | ||
| U | 5.76 | 57.30 | Reciprocal of Q | |
| M | 1/p | 3.18 | .3183 | |
| g | gF | 9.81 | Gravitational acceleration m/s2 | |
| g | gE | 3.22 | 32.2 | Gravitational acceleration ft/s2 |
| EHP | 7.46 | 746 | English horse power -watts/HP- |
The example below shows three gauge points (p, r' and C1) on a Danish slide rule.

The Gunner's Mark
For small angles:
tan q » sin q » q
radians
The Gunner's mark makes use of this.
In the diagram set the the angle in minutes on the D scale against the auxiliary base in feet, the base in yards is read on the C scale against the Gunner's Mark on the D scale.
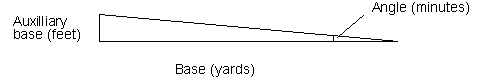
In effect the Gunner's mark (1146) is given by:
1/1146 = (p x 3) / (180 x 60).
| Return to | Basics in A-to-Z |