
INSTRUCTIONS
for Mechanical and Electrical Engineers,
Students of Technical Universities,
Engineering Colleges, Polytechnics
with enlarged
scale range
 |
INSTRUCTIONS
|
|
| Precision Slide Rule for Mechanical and Electrical Engineers, Students of Technical Universities, Engineering Colleges, Polytechnics |
No. 2/83N, 62/83N with enlarged scale range |
|
The CASTELL 2/83 N with enlarged scale range
Many satisfied users of the 2/83 N slide rule, in a sprit of constructive criticism,
have suggested that the arrangement of the scales on the front and back should be
improved. Our Development Department has taken advantage of the experience gathered during
these last few years and utilised the latest knowledge acquired. Apart from numerous minor
improvements, the scales A, B, DI (on the front) and LL00, CI, D and LL0
(on the back) have been added.
Contents
The scales of the pocket slide
rule 62/83 N with graduation length 5" (12.5 cm)
| From graduation figure 1 to graduation figure 1.2. (Section of scale reading 1 to 2) |
From graduation figure 2 to graduation figure 3. (Section of scale reading 2 to 5) |
From graduation figure 5 to graduation figure 7. (Section of scale reading 5 to 10) |
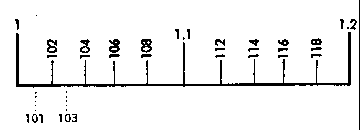 |
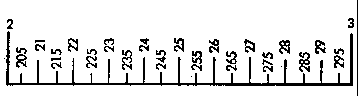 |
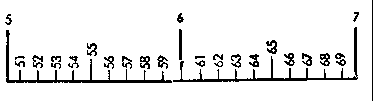 |
| Each interval is equivalent to 2 sub sections. An accurate reading can be taken of the values corresponding to 3 places. The odd numbers are obtained by halving the distance between two graduation marks. | Each interval is equivalent to 5 sub sections. This provides an accurate reading of the values corresponding to 3 places, if the last figure is a 5. | Each interval is equivalent to 10 sub.sections. This provides an accurate reading of the values corresponding to 2 places, which more over are identified by graduation marks. |
| Other intermediate values must be estimated. Example: To set to 318, first find 3.1.7.5 by halving the distance between 315 and 320, and then move the cursor line slightly to the right. | ||
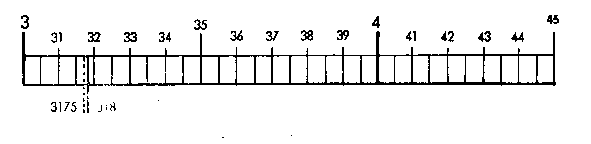 |
||
The Scales of the Slide
Rule 2/83 N
All scales are marked with reference to the basic scales C and D. At the
right.hand end of the slide rule they bear the mathematical formula based on the numbering
of the basic scales.
The cursor, entirely surrounding the slide rule, enables each stage of the calculation to
be connected with the next, throughout all the scales on the front and back of the slide
rule.
| Scales on the front of the slide rule: | |||
| 1st tangent scale | T1 | tan 0.1 x (cot) | on upper body |
| 2nd tangent scale | T2 | tan x (cot) | |
| cube scale | K | x3 | |
| fixed square scale | A | x2 | |
| fixed x.folded scale | DF | px | |
| movable x.folded scale | CF | px | on slide |
| movable square scale | B | x2 | |
| reciprocal x.folded scale | CIF | 1 :px | |
| reciprocal basic scale | CI | 1 : x | |
| movable basic scale | C | x | |
| fixed basic scale | D | x | on lower body |
| fixed reciprocal basic scale | DI | 1 : x | |
| sine scale | S | sin 0·1 x (cos) | |
| arc scale for small angles | ST | arc 0.01 x | |
| Pythagorean scale | P | Ö(1 . (0.1 x)2) | |
| Scales on the back of the slide rule: | |||
| exponential scales for negative exponents | LL03 | e.x | on upper body |
| LL02 | e.0·1 x | ||
| LL01 | e.0.01x | ||
| LL00 | e.0·001 | ||
| 2nd fixed root scale | W2 | (Ö10)x | on slide |
| 2nd movable root scale | W2' | Ö(10x) | |
| reciprocal basic scale | CI | 1 : x | |
| mantissa scale | L | ½ log x | |
| movable basic scale | C | x | |
| 1st movable root scale | W1' | Öx | |
| 1st fixed root scale | W1 | Öx | on lower body |
| fixed basic scale | D | x | |
| and exponential scale | LL0 | e0.001x | |
| additional exponential scales for positive exponents | LL1 | e0·01x | |
| LL2 | e0·1x | ||
| LL3 | ex | ||
How to read the scales with graduation length of 10 inches, e.g. C, D, CF, DF, CIF
The following should be noted:
The slide rule does not show the actual place of decimals to which a number belongs. For example, the 6 shown on the slide rule may equally well denote 6, 0.6, 60, 600, 6000 or 0.006, and so forth.(An exception is provided by the exponential scales) The position of the decimal point is ascertained afterwards, by a rough calculation with round figures. In most practical calculations it is known in advance, so that no further rules for determining the decimal point are required. It is the basic scales C and D that give the clearest idea of the way in which the scales are sub.divided. Once familiar with the graduation of these two scales, we shall be able to understand the others likewise.
All scales marked in red run in the opposite direction (reciprocally) from right to left, the exceptions being the extended supplementary graduations which are provided to enable a calculation to be continued in the case of border line values just below 1 (beginning of graduation) or just above 10 (end of graduation).
Let us now have a look at the basic scales C and D on the front of the slide rule, the reading . and setting . exercises being carried out by means of the long cursor line or the index.1 (beginning of scale) or index.l0 (end of scale), as the case may be.
| A section of the graduation.range from I to 2 (Scales C and D) | 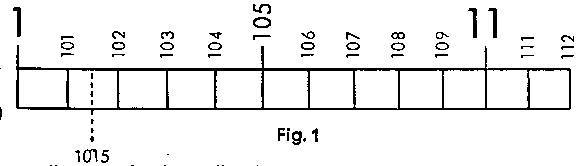 |
From guide.number 1 to guide.number 1·1 10 sub.divisions of 10 intervals each (= 1/100 or 0·01 per graduation mark) |
| Here an accurate reading can be immediately taken to 3 places (e.g. 1.0.1). By halving the space between two graduation marks, 4 figures can be accurately set (e.g. 1.0.1.5). In all cases the final number must then be a 5. | ||
| A section of the graduation.range from 2 to 4 (Scales C and D) | 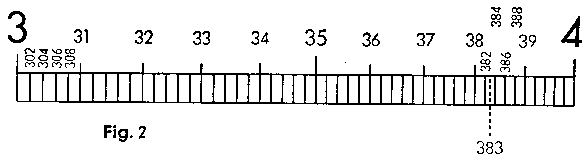 |
From guide.number 3 to guide.number 4 10 sub.divisions of 5 intervals each (= 1/50 or 0·02 per graduation mark) |
| Here an accurate reading can be immediately taken to 3 places (e.g. 3.8.2). The last number is then always even (2, 4, 6, 8). If the intermediate spaces are halved, this provides the uneven numbers (1, 3, 5, 7, 9) as well (e.g. 3.8.3). | ||
| A section of the graduation.range from 4 to 10 (Scales C and D) |
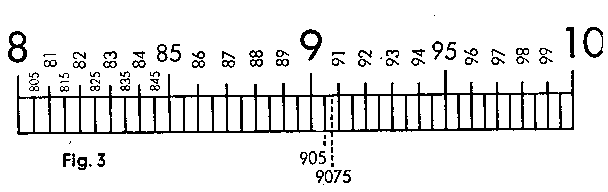 |
From guide.number 8 to 9 and guide.number 10 10 sub.divisions of 2 intervals each (= 1/20 or 0·05 per graduation mark) |
| Here an accurate reading can be taken to 3 places, when the last number is a 5 (9.0.5). By halving the intermediate spaces it is even possible to take an accurate reading to 4 places. Here again the last number is always a 5 (9.0.7.5). | ||
How to read the scales with
graduation length of 20 inches: W1 W1' W2 W2'
These scales are provided along the edges and adjacent edges of the slide, on the
back of the slide rule, and run from 1 to 3.3 at the bottom and from 3 to 10 at the top.
Their use results in doubled accuracy. They are sub.divided differently, however, from the
scales on the 10 inch graduations.
Graduation range from 1 to 2.
This section is first of all divided into ten sub.divisions, marked 1·1, 1·2, 1·3,
1·4... 1.9. Each of these, in turn, is divided into ten further
sub.divisions, but the latter are not numbered, owing to lack of space. Finally, a small
stroke is also provided to show the exact centre between these graduation marks. Readings
can be taken as follows: 1.1.2.5, 1.3.1.5, 1.4.4.5, 1.5.2.5, 1.7.1.5... 1.9.7.5.
Graduation.range from 2 to 5.
Hero again, this section is first of all divided into tenths, but they are not
numbered, except for the graduation marks corresponding to the values 2, 2.5, 3, 3·5. 4,
4.5 and 5. The user must recognise the remaining tenths for himself, i.e. the values 2·1,
2·2, 2.3 ... to 4·7. 4.8, 4·9.
Further tenths are entered In between these tenths but without "marked centres".
We thus hove the following values, starting with 2 and without using the decimal point:
2.0.0, 2.0.1, 2.0.2. 2.0.3, 2.0.4, 2.0.5, 2.0.6, etc., up to 4.9.7, 4.9.8, 4.9.9, 5.0.0.
Graduation.range from 5 to 10.
In this range, the tenths first of all appear, as before, but in between these
it is only the fifths that are provided.
Starting with 5, we thus have the following graduation marks: 5.0.0, 5.0.2, 5.0.4, 5.0.6,
5.0.8, 5.1.0, 5.1.2, etc. up to 9.9.6, 9.9.8, 1.0.0.
The reading range of these scales exceeds by far these possibilities. Further intermediate
values, however, must be estimated.
| Multiplication | a · b |
This is chiefly carried out with the main scales C and D of the front of the slide
rule.
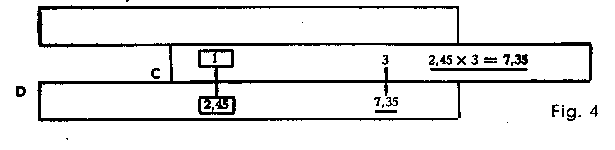 |
Example: 2.45 x 3 = 7.35 Set the 1 of the slide of the rule (C 1) above the 2·45 on the lower scale of the slide rule (D 245), move the cursor line (Important: Whenever the cursor line is mentioned in this and the following chapters, this will always refer to the long, central hairline on the front and the back of the cursor.) Into position above the 3 of the lower slide scale (C 3) and read the product . 7·35 . underneath the cursor line on the lower scale of the slide rule (D 735). Multiplication with Scales A and B: see below |
Example: 2.04 x 3.18 = 6.487. Place C 1 above D 2.04, place the cursor line above D 3.18, and read the result . 6.49 . on D, likewise underneath the cursor line.
Example: 11.45 x 4.22 = 48·35. Place C 1 above D 11.45, place the cursor line above C 4.22, and read the result . 48·35 . on D, likewise underneath the cursor line.
In calculations on the lower scales C and D it sometimes happens that with the setting C 1 above the first factor on scale D the slide projects too far to the right, so that it is no longer possible to set the second factor on C.
Transposing of the slide
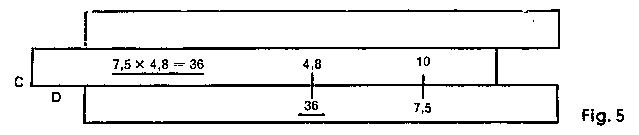 |
Example: 7.5 x 4.8 = 36 in this case the slide is pushed to the left until the beginning C 1 is replaced by the end of the slide C 10 (marked 1) above the first factor on scale D. |
This operation is termed transposing the slide. It can be avoided if, in case of need, C 10 (end of slide) is immediately placed above the first factor. An experienced user knows at once which method of setting to adopt, i.e. "beginning of slide, C 1, above first factor" or "end of slide, C 10 (marked 1), above first factor".
Examples for practice:
Setting: "Beginning of slide C 1 above first factor": 1.82 x 3.9 = 7.1; 0.246 x
0.37 = 0.091; 213 x 0·258 = 54·95
Setting: "End of slide C 10 above first factor": 4.63 X 3.17 = 14.68; 0.694 X
0.484 = 0.336
This operation of transposing of the slide is not necessary, in practical use, with the
"x.displaced scales" CF, DF, in con junction with scales C and D (see below).
| Multiplication with Scales C and D of back of slide rule | a · b |
Multiplications can also be carried out with the scales C and D on the back of the
slide rule. It is necessary, however, to use the main cursor line for all settings and
reading.
Example: 3.63 x 1.41 = 5.12. Use the cursor line to place C1 above D 3.63, then
move cursor line to C 1.41 and read below on D the result, 5.12.
The C and D scales of the back of the slide rule are especially convenient for compound
calculations, in conjunction with the root scales (see below) and the exponential scales
(see below).
| Division | a / b |
Use the cursor line to place the numerator on D and the denominator on C opposite each
other; the result can then be found underneath the beginning of the slide of the rule, C
1, or under the end of the slide, C 10. Division with A and B: see below.
Example: 9.85 ¸ 2.5 = 3.94
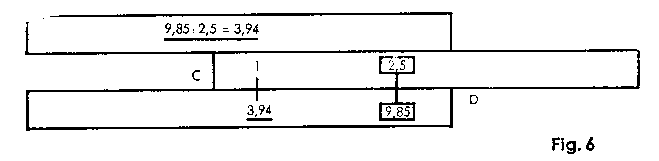 |
First bring the cursor line into position above the numerator, 9.85, on the lower scale D of the body of the slide rule, then place the denominator 2.5 (on the C graduation) underneath the cursor line. The numerator and the denominator are now level with each other, and underneath the beginning of the slide, C 1, the result 3·94 can be found on scale 0. |
Examples for practice: 970 ¸ 26·8 = 36.2; 285 ¸ 3.14 = 90.7; 7500 ¸ 835 = 8.98; 0.685 ¸ 0.454 = 1·509; 68 ¸ 258 = 0.264
| Combined Multiplication and Division | (a · b · c) / (d · e · f) |
These calculations are mainly carried out with the scales C and D on the front of the
slide rule.
Example: (13.8 x 24.5 x 3.75)/(17.6 x 29.6 x 4.96) = 0.491
Always start with the division and then let multiplication and division alternate. No
readings need be taken of the intermediate results. We thus first use the cursor line to
place D 1.3.8 and C 1.7.6 level with each other (division). No reading is taken of the
result, approximately 0.8 underneath C 10 on D, and the multiplication by 24.5 is carried
out immediately, by placing the cursor line on C 2.4.5. The result (about 1.9 on D) is
then divided by 29.6, by leaving the cursor line in its present position and bringing C
2.9.6 into position underneath it. The next operation is the multiplication of the result
(0.65 underneath C 10 on D) by 3.7.5, the final operation being the division by 4.96, In
the same manner. The result 0.491 can then be found underneath C 10 on D.
Examples for practice: (38.9 x 1.374 x 16.3)/(141.2 x 2.14) = 2.883; (1.89 x 7.68 x
8.76)/(0.723 x 4.76) =36·95
| Formation of Tables | a / b : c / d : e / f |
For forming a table, first set the slide rule the required "equivalence";
mutual conversions of measurements, weights and other units can then be carried out. Once
we establish that 1 inch = 25.4 mm, for example, C 1 Is placed over the
corresponding value; for 75 lbs = 34 kgs., the two values are placed opposite each
other on C and D.
Example; To convert yards into metres. 82 yards = 75 metres.
 |
Place C 75 above D 82. This produces a table, and reading may be taken
as follows: 42 yards are 38.4 metres; 2.8 yards are 2·56m; 640yards are 585 m; 16m are 17.5 yards; 128 m are 140 yards, and so forth. |
Examples for practice:
| 1 inch = 25.4 mm ("Equivalence": 26" . 66
cm). Place C 1 (left.hand 1 of C) above D 2.5.4 (2.5.4 on D) and take the following
readings by the aid of the cursor line: 17 inches = 43.2 cm 38 inches = 96.6 cm |
1 metre of material costs DM 45. Place C 1 above D 45 and take the
following readings with the cursor line: 3.20 metres of material costs DM 144. 2.40 metres of material costs DM 108. |
Exchange rate: US$ 1.. = DM 4. Place C 10 above D 4.0.0 and take the following readings with the aid of the cursor line: US$ 2.61 = DM 10.44 US$ 4.73 = DM 18.92 |
If, in the formation of tables, It is no longer possible to set and read off individual
values, because the slide of the rule projects too far, we again transpose the slide, i.e.
"hold the setting" by placing the cursor line over C 1. The slide is then pushed
along until C 10 replaces C 1.
Calculations with Scales CI and DI
The movable scale CI
This is sub.divided from 1 to 10, so that its graduation system corresponds to that of
the scales C and D, but it takes the opposite direction and is therefore coloured red. Its
use enables various types of calculation to be performed. (This manipulation can be
arrived by using scales CF and DF, as explained below).
| 1) If, for a given number a, the reciprocal 1 ¸
a is required, this is set on C or CI and the reciprocal read off, above it, on CI or on
C. The reading can be taken without adjusting the slide, with the use of the cursor alone.
Experienced slide.rule users can also operate without zero setting, if they only refer to
scales C and CI (and, above all, do not allow themselves to be confused by the scale D
appearing below). Example: 1 ¸ 8 = 0·125, 1 ¸ 2 = 0.5; 1 ¸ 4 = 0.25; 1 ¸ 3 = 0.333. |
1/a |
| (2) Multiplication likewise can be carried out with the scales D and
CI. (Division by reciprocal = multiplication). This method is popular with many
slide rule users. Example: 0.66 x 20.25 = 13.37. |
a x b |
| 3) The following shows how simply products with a number of factors
can be calculated: Example: 0.66 x 20.25 x 2.38 = 31.8. |
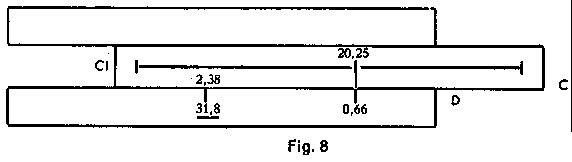 |
a x b x c |
Multiply the first two factors as above; with C 1 above 13.37 (intermediate results) we immediately have the first setting required for multiplication by the next factor (by the method learnt first at the top of p. 8). Consequently, we now bring the cursor line into position above C 2.38. The result, underneath it, on D, is 31.8. This could be followed immediately by a further multiplication, by bringing the next factor, on CI, into position underneath the cursor line and reading off the result, under C 1 (or C 10, as the case may be), on D. We thus multiply alternately with the aid of D and CI (see above, for method) and with the aid of C and D (first method - see above).
| (4) Combined Multiplication and Division. This likewise can be advantageously performed with the scale CI. Example: 36.4 / (3.2 x 4.6) = 2.473 First the division, i.e. cursor line above D 3-6-4, then C 3.2 underneath the cursor line. (Intermediate result: 11.37, underneath C 1). With CI above D 11.37, we already have the first setting for the subsequent multiplication by 1/64 which is performed by the aid of the scale CI (1/c). The cursor line is thus now brought into position above CI 4.6, the result - 2.472 - likewise being found beneath cursor line. Example for practice: 44 / (4.85 x 3.66) = 2.48; 4.774 x /(0.63 x 1.24) = 6.11; 23.1 /
(2.73 x 17.9) = 0.473 |
a / b x c |
The fixed scale DI
This is subdivided like Scale D but runs in the opposite direction and
is therefore coloured red.
1) In conjunction with D, DI gives the reciprocal. It is set and read with the cursor
line. This offers the advantage that the two scales are provided permanently opposite each
other, forming a table.
2) As with CI (see above) multiplication can also be carried out by the aid of DI. (Result
appears above D l or D 10).
Example: 6.43 X 2.96 = 19.03. Cursor line above D l 6-4-3, second factor 2-9-6 on C under cursor line, read off result 19.03 above D 1.
3) It is above all with the function 1/(a x b) that the Scale DI is of advantage.
Example: 1/ (0.284 x 0.12). First carry out the multiplication on C and D, i.e. C 1 above D 2-8-4, cursor line above C 1.2; the intermediate result (0.03408) appears underneath, on D; the result, 29.34, Is likewise found on DI, underneath the cursor line on D.
The use of DI in trigonometrical calculations should also be noted.
Calculation with the Square Scales A and B
Multiplication and division can also be carried out on Scales A and B. For this purpose, use is made of the long cursor line.
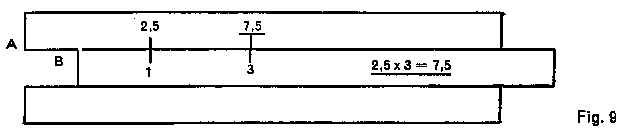 |
Example: 2.5 X 3 = 7·5 Place the long cursor line above A 2.5, move B 1 into position under the cursor line, move the latter into position above B 3, and find above it, on A, the result 7.5. |
For division, the numerator on A and the denominator on B are first of all placed opposite each other by the aid of the cursor line (first of all above the numerator on A), after which the result can be road off above B 1 or B 10. For this purpose, however, the cursor line must again be used.
| Squares and Square Roots | a2 |
The square of any number is obtained by setting the cursor line over this number on scale D, the result is shown above it on scale A, under the cursor line. We can, however, also use the first and last graduation marks at either end of the scales.
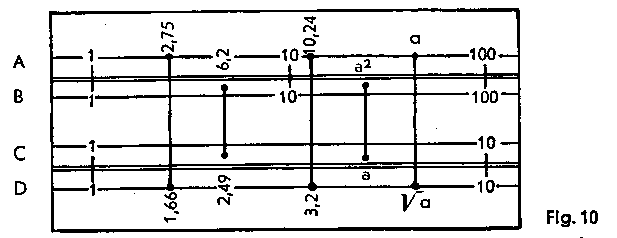 |
Examples: 1.662 = 2.75 2.492 = 6·2 3.222 = 10.24 |
| When setting and taking readings one should get accustomed to work only with groups of figures and determine the decimal value thereafter by a rough estimate. The figures should be rounded off liberally, as this rough estimate is merely made to avoid getting tenfolds or tenths of the actual cursor. | Öa |
Further examples: 1.3452 = 1.81; 4·572 = 20.9; 0·7652 = 0.585; 67.32 = 4530.
Square Roots are extracted by reversing this procedure. If, therefore, the cursor line is placed on a figure on A, then the square root can be read off on D, underneath it. Extracting square roots is, however, not as simple as finding the square, as may be seen from the following example: Extract Ö3.65. Place the cursor line on A 3.65 and find underneath on D the square root 1·91. As we have learned that the position of the decimal point is not shown on the slide rule, we could also set the cursor line over A 36.5 (in the second half of scale A between 10 and 100). Underneath we would find the root 6·04, which is obviously the wrong result.
Before extracting the square root, we must decide If the number must be set on the right or the left half of the scale. At the left are the numbers from I to 10, and at the right those from 10 to 100.
If the number lies outside the scale range 1 to 100, it should be factorised by
hundreds to bring significant figures within these limits.
Examples: Ö1936. We factorise Ö1936
= Ö(100x19.36) = 10 x Ö19.36 = 10
x 4.4 = 44
Ö0.00378 = Ö(37.8/10 000) = Ö37.8/100 = 6.15/100 0.0615
Ö145.8 = Ö(100 x 145.8) = 10 x Ö1.548 = 10 x 1.207 = 12.07
Ö507 000 = Ö (10 000 x 50.7) = 100
x Ö50.7 = 100 x 7.12 = 712
Square and square root can also be determined by the aid of the root scales, with greater accuracy (see below).
| Cubes
and Cube Roots (Cube scale K' see Immediately below) |
a3 |
The cube scale K consists of three equally long units 1-10, 10-100, 100-1000, each one third of the length of the C, D and CI scales. To find the cube of a number, the cursor line is set to the base number on scale C and the cube of that number is read off on K.
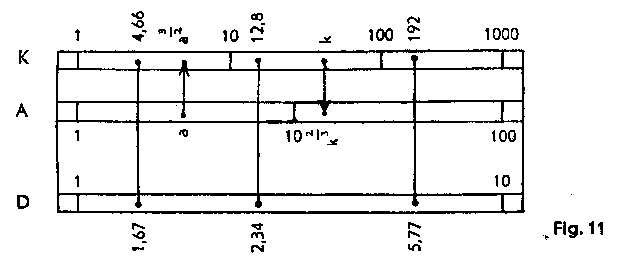 |
Examples: 1·673 = 4·66 2·343 = 12·8 5·773 = 192 |
| When extracting a cube root, we use the opposite procedure. We set on K and read off on D. | 3Öa |
Examples:
3Ö4.66 = 1.67; 3Ö29.5 = 3.09; 3Ö192 = 5.77If the cube scale K is employed with the Square Scale A, powers with the exponents 2/3 and 3/2 can be obtained with the aid of the cursor line.
| Example: 7.53/2 = 20.5 Set the cursor
line over 7.5 on A and read underneath on K the answer 20.5. Example: 1322/3 = 25.9 Set the cursor line over 132 on K and read underneath on K the answer 2.69. |
a3/2 |
Calculations with the Scales
CF, DF and CIF
| (1) Formation of Tables | a / b : c / d : e / f |
Since with the " folded" scales CF and DF, the value 1 is more or less in the centre, they provide an advantageous means of continuing the calculations, in the formation of tables, thus avoiding the necessity for transposing of the slide when calculating on C and D.
Example: 75 lbs = 34 kgs. Place C 3-4 above D 7-5; this provides the conversion from English lbs. into kilogrammes.
Beyond 50 kgs. however (C 5), no further readings can be taken. Here we switch over to the upper scales CF and DF, and the slide rule can be set to the necessary values with the aid of the cursor line.
If the "equivalence" In question (e.g. 75 lbs = 34 kgs.) is not known, but
the formula 1 lb = 0.454 kgs., for example,
is known, then CF 1 is placed underneath DF 4-5-4, and this likewise provides the
conversion from lbs Into kgs.
| (2) Multiplication | a x b |
If; in multiplication on C and D, the second factor proves "unsettable", or if the method of transposing of the slide has to be adopted, this can be avoided by setting CF to the second factor and taking a reading of the result on DF.
Example: 2.91 x 4 = 11.64. Place C 1 above D 2-9-1, and place the cursor line above CF 4. Above it, on DF, a reading may be taken of the result (11.64).
Examples for practice: 18.4 x 7.4 = 136.1; 42.25 x 3.7 = 156.3; 1.937 x 6 = 11.62.
| (3) Multiplication and Division by p | a x p |
The change-over from the C and D scales to the CF or DF scale can be carried out direct with the cursor line and results in multiplication by p.
Example: 1·184p = 3·72. With the slide in the zero position (C 1 above D 1 and C 10 above D 10) the cursor line is brought into position above D 1-1-8-4, and the result - 3.72 - is read on DF, likewise beneath the cursor line.
The converse operation results in division by p.
Examples: 18.65/p = 5·94. Place the cursor line above DF 1-8-6-5 and read the result - 5·94 - on D.
Examples for practice:
Area of an ellipse: F=a x b x p ; F=5·25 x 2·22 x p = 36.6.
Place C 10 above D 5-2-5, bring the cursor line into position above C 2-2-2, and read the
result - 36.6 - on DF, without
any need to take a reading of the intermediate result - 11.65 - on
D.
Length of a circular arc: s = a r p
/ 180 ; s =26.2 x 352 x p / 180 = 161
We start with the division, i.e. use the cursor line to bring C 1-8 and D 2-6-2 opposite
each other. No reading need be taken of the intermediate result 0.1455 (under C 1). The
multiplication by 352 is carried out by placing the cursor line under 3-5-2. (Intermediate
result: 51·2, on D). The multiplication by is again carried out by switching over to the
top part and by finding the result 161 underneath the cursor line on DF.
(4) The CIF Scale operates in conjunction with CF and DF just as CI does with C and D scales.
Examples for multiplication by a number of factors:
2.23 x 16·7 x 1.175 x 24·2 = 1059.
Solution: CI-2·23 placed above D-16·7 by the aid of the cursor line; the latter is
placed above CF-1·175. CIF 24.3 under the cursor line. Read result, 1059, on DF, above CF
1.
0·53 x 0·73 x 39.1 x 0·732 = 11.07.
Solution: CI-0.53 placed above D-0·73 with the aid of the cursor line; the latter is
placed above CF-39·1. CIF 0.732 underneath cursor line; Read the result 11.07, on DF,
above CF 1.
Calculations with the
Pythagorean Scale P
This scale represents the function y = Ö(1 - (0.1x)2);
it operates in conjunction with D (= x), of which the values must be read from 0.1 to 1.
The graduation runs in the opposite direction and is therefore coloured red.
If D is set to the value x, then the corresponding value y = Ö(1 - x2) can be read on P; conversely, If D is set to y. the value x = Ö(1 - y2) can be read on P.
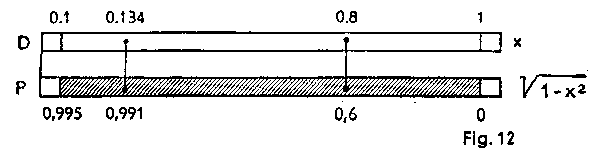 |
Example: y =Ö(1 - 0.82) = 0·6;
x = Ö(1 - 0.62) = 0.8 If, therefore, we set D to x = 0.8, we find the value y = 0·6 on P, and vice versa. Example: sin a = 0·134; cos a = 0.991 If D is set to the sine, the cosine is obtained on P, and vice versa. |
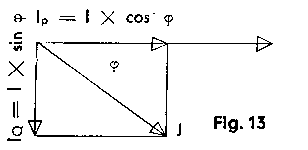 |
Example: Calculate the active current and the reactive current of a circuit absorbing 35 A with a cos j of 0.8. Ip = I x cos j = 35 x 0·8 = 28 (A);IQ =I x sin j = 35 x 0·6 = 21 (A). |
Place C 35 above D 10 and find at D 8 (for a cos j of 0.8), on C, the active current 28; underneath D 8 the value 0.6 (i.e. sin j = 0·6) is at the same time found on P. If the cursor is now moved into position onto D 6, the wattless current 21 is found above it on C.
Example: apparent power 530 kVA, effective power 428 kW. To find reactive power and cos
j:
Place C 530 above D 10, bring cursor into position above C 428, find the value (0.807) for
the cos j underneath it, on D; trace this value on P, by means
of the cursor, and find the required reactive power - 313 kW -
above it, on C.
Roots of numbers only just below 1 and 100 can be found by means of this scale with an increased degree of accuracy:
Example:Ö0.925 = Ö(1- 0.075 = Ö(1-(0.2739)2)
= 0.9618. We form the equation: 1 - z = 1 - 0.925 = 0.075.
Set the cursor on D 75 and find 0.2739 on W1 the cursor is now placed on D 2739
and the reading 0.9618 Is taken below it, on P.
Calculations with the
Trigonometrical Scales S, T1 and T2
The trigonometric scales T1, T2 and S are
sub-divided decimally; in conjunction with the basic scales C and D they indicate angular
functions or, if read in the reverse direction, the angles.
When the T1, T2 and S scales are used in conjunction with the D,
P and CI scales, as trigonometrical tables, the following must be noted:
The S scale, when the black figures are read, provides, in conjunction
with the D scale (black), a table of sines; the same
applies when the red figures are read, in conjunction with the P scale (red).
In the case of small angles the first procedure is the more accurate, while in the case of
wide angles preference is given to the second method.
The S scale, when the red figures are read, provides, in conjunction with
D (black), a table of cosines; the same applies when the black
figures are read, In conjunction with P (red). In the case of wide angles
the former process Is the more accurate, while with small angles preference is given to
the latter method.
The two T scales, when the black figures are read, provide, in
conjunction with the D scale (black), a table of tangents; the same
applies when the red figures are read, in conjunction with CI (red).
The two T scales, when the red figures are read, provide, in conjunction
with the D Scale (black), a table of cotangents; the same applies when
the black figures are read, in conjunction with CI (red).
| sin 13° = 0.225 | / | S 13° (black) -D 0.225 (black) | These settings are carried out with the slide rule set at zero, by the aid of the cursor line. |
| sin 76° = 0.97 | / | S 76° (red) - P 0.97 (red) | |
| cos 11° = 0·982 | / | S 11° (black) - P0·982 (red) | |
| cos 78° = 0.208 | / | S 78° (red) - D 0.208 (black) | |
| tan 32° = 0.625 | / | T1 32° (black) - D 0.625 (black) | |
| tan 57° = 1·54 | / | T257° (black) - D1.54 (black) | |
| cot 18° = 3.08 | / | T218° (red) - D3·08 (black) | or T1 18° (black) - CI 3.08 (red) |
| cot 75° = 0.268 | / | T1 75° (red) - D 0.268 (black) | or T2 75° (black) - CI 0.268 (red) |
To proceed from the sine of angle to its cosine (or vice versa) no reading need be taken of the angle. These pairs of values are to be found one under the other on D and P. The reading of the angle can also be avoided when proceeding from the tangent to the cotangent, as these pairs of values are to be found one under the other on C and CI. An intermediate reading of the angle need only be taken when proceeding from the sine or the cosine to the tangent or cotangent. Since, when reading the functions, these can be obtained either on D or on CI, multiplications and divisions can in many cases follow immediately. It is only when the reading is taken on P that the value must be transferred to the main scales.
Further examples of the use of the trigonometrical and Pythagorean scales In a right-angled triangle.
| (1) Example: Given: a = 2; b = 3. Find: c and a
; Formula: a x (1/b) = tan a ; a x (1/c) = sin a; (2) Example: Given a = 8; b = 20. Find c and a (3) Example: Given: a = 20; b = 8. Find c and a |
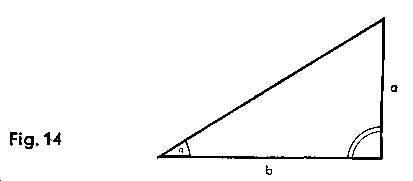 |
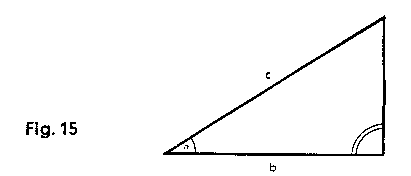
| (4) Example: Given: c = 5; a = 36.87°;
Find: a and b. Formula: a = c x sin a; b = c x cos a C 5 above D 10, cursor on 36.870 on sine scale; value for a (3) found on C. The value (0.8) for cos a is found on the P scale at the same time, and the cursor moved to D 8. The value for b, i.e. 4, can now be read on the C scale. (5) Example: Given: c = 21.54; b = 20. Find: a and a C 2154 above D 10, cursor to be placed at C 2 (for b = 20) and find the value (21.80) for a on the cos scale, but take the reading 0·372 at the same time from the P scale. Push the slide along to the left by one scale-length. Move cursor to D 0.372 and find the value for a, i.e. 8, on C. |
 |
| For the scalene triangle we have the formula a/ sin a = b / sin b = c / sin Example: Given: a = 38.3; a = 52°; b = 59°; g = 69°; Find: b and c. Place C 383 above S 52°; above S 59° and S 69° we now find the results (41.7 and 45.4) on C. |
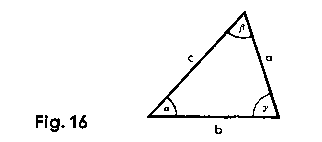 |
| The Small-Angle Scale ST | and the Mark r on Scales C and D |
| For the functions of small angles from 0.55 to 6° the lower part of
the body of the slide rule bears the ST Scale ( arc 0.01 x) with the formula sin a » tan a » arc a The ST scale operates in conjunction with scale D (or C). All further calculations in this column are carried out solely with the aid of the cursor line. |
The functions of small angles can also be determined with the
mark r = p/180 = 0.01745
in accordance with the formula: |
| Examples for practice: sin 2.5° » tan 2.5° » arc 2.5° » 0.0436; sin 0.4° » tan 0.4° » arc 0.4° » 0.00698; sin 0.0052° » tan 0.0052° » arc 0.0052° » 0.0000908 |
|
| Set the angle-values on the arc-scale ST. Read the functions from scale C (with zero setting) or from scale D (with the aid of the cursor line). | Example: sin 3° » tan 3° » arc 3° = 0·0524. Place beginning of slide, C 1, above D 3; the
result 0.0524 can now be read on D, underneath r on C. |
| For calculation of the cosine and cotangent functions of angles over 84.5° | |
| Example: cos 88° = sin 2° » arc 2° =
0·0349 cot 86·5° = tan 3·5° » arc 3.5° = 0.0612 Place the cursor line above the angle-value on the scale ST, and read the result from C (with zero setting) or on D, underneath the cursor line. |
Example: cos 88° = sin 2° » arc 2° 0 x
2 = 0·0349 cot 86·5° = tan ·5° » arc 3·5° » r x 3.5 = 0.0612 This is a simple multiplication; we thus place the beginning of the slide, C 1, above r on D, then the cursor line above the second factor on C, and read the result underneath it, on D. |
| For conversion of arcs into angular degrees: Examples for practice::arc 6.28 = 360°; arc 1.11 = 63.5°; arc 0.04 = 2.29°; arc 0.007 = 0.402°; arc 0.64 = 36.7°; arc 0.32 = 18.35° |
|
| Set the arc on the C or D Scale. The degrees can be read from the arc-scale ST (with the aid of the cursor line). | C 1 or C 10 above the r mark on D, then place cursor line above the arc-measurement on D. The angular degrees can be read above it, on C. (Increased accuracy is achieved when using the r marks on scales W1 and W1'.) |
Calculations with Complex Numbers
Two complex values X = 7.5 e i p/8 and V = 3.4 e i p/10 are to be added. They are first of all concerted, in accordance with the Euler Equation
R x e ij = R (cos j + i sin j ) to the form (a + i b).
For calculations on the slide rule it is best to express these magnitudes vectorially:
as follows:
= 7.5/22.5° and V = 3·4/18° we can now calculate as follows:
(1) Place C 75 above D 10, move cursor to S 22·5° and read the value of b1 (2.87)
on C. At the same time find the value of cos j (0·924) on the
P scale. Move cursor to D 924 and find the value of a1 (6.93) on C.
(a1 + i b1) = 6.93 + i 2.87.
(2) Place C 34 above D 1, move cursor to S 18°, and find the value for b2 (1.05)
on C. At the same time, find the value for cos j (0.951) on P.
Move cursor to D 951 (red extended graduation) and find the value for a2 (3.24)
on C.
(a2 + i b2) = 3·24 + i 1.05
a1 + a2 = 6.93 + 3.24 = 10.17 and i (b1 + b2)
= i(2.87 + 1.05) = i 3·92.
The result is thus: = (10.17 + i 3.92)
If the result is to appear in vectorial form, we calculate thus:
Place C 10 above D 392, move cursor to CI 1017, and find the value of j
(21.07°) above it, on T1 (Tangent scale). We then move the cursor to 21.07 on
the sine scale S and find the value for V (10.92) above it, on
CI.
Thus = (10.17 + i 3·92) = 10·92/21·07°
and with r x j =
arc j, (arc j =0·368) we
have = 10·92/21·07° = 10.92 e i 0.368
Example for the use of the T2 scale: V = 192 - i
256
Place C 10 above D 256, move cursor to CI 192. On T2 we obtain the angular
value 53.1°. Then place C 1 above D 256 and move the cursor.line to 5 53.1. On CI we
obtain the result 320.
As the numb is in the IVth Quadrant, the angular value must be negative.
The multiplication of complex numbers is carried out in accordance with the equation:
X
· V = X · e i j· Y · e i y= XY · e i (j+y) = XY / j+y| Examples for (I): 1.635 x 5.365 = 8.77 Solution: Black Index-1 (W1'-1) above W1-1·635. Cursor line above W2'-5·365; find result (8.77) on W2. |
809 x 1.414 = 1144 Solution: Black Index-l0 (W2'-10) underneath W2-809. Cursor line above W1-1·414; find result (1144) on W1. |
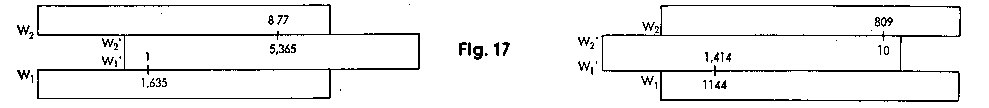 |
|
| Examples for practice: 236 x 4.06 = 958; 2.34 x 0·409 = 0.957 Examples for (II): 1·804 x 7.73 = 13·95 Solution: Red Index-mark above W1-1·804; cursor line above W2'-7·73; at the same time find the result (13.95) underneath the cursor line, on the opposite scale W3. |
777 x 66·3 = 515; 5·165 x 0.2265 = 11699 50.45 x 4·64 = 234.1. Solution: , Red index-mark under W2 50.45; cursor line above W2'-4·64; at the same time find the result (234.1) underneath the cursor line on the opposite scale W1. |
 |
|
| Examples for practice: 14·78 x 0·945 = 13·97; 29.4 x 123·6 = 3634 | 0.395 x 0.562 = 0.222; ·885 x 19·425 = 75·47 |
Division
| Examples for (I): 3·08 4- 2·135 = l·443. Solution: With the aid of the cursor line, place W1-3·08 and W3'-2·135 opposite each other, and find the result (1.443) on W1, underneath the black index-l. | 42·3 4- 71-7 = 0·589. Solution: With the aid of the cursor line, place W2-42·3 and W2'-71·7 opposite each other, and find the result (0-589) above the black index-10, on W2. |
 |
|
| Examples for practice: 2·975 ¸ 18·65 = 0.1595; 2.075 ¸ 148.25 = 0014; 48.65 ¸ 79.05 = 0.6155; 5·55 ¸ 0·692 = 8·02 | |
| Examples for (II): 374·5 ¸ l·5675 = 238. Solution: cursor line above W2-374·5; W1'-1·5675 under cursor line; the result, 238, is read on W1 underneath the red index-mark. | 23.77 ¸ 65.67 = 3.615. Solution: cursor line above W2-23·77; W2'-65·67 under cursor line; the result, (3-615) is found on W2, above the red index-mark. |
 |
|
| Examples for practice: 689.5 ¸ 2.505 = 275.2; 432·5 ¸ 1·845 = 234·4; 1·965 ¸ 44·45 = 0.0442; 8·37 ¸ 1.1575 = 7.23 | |
Formation of Tables
Example:
"Equivalence": 82 yards = 75 metres. By means of the cursor line place W2-82
and W2'-75 opposite each other. The following readings can now be taken,
likewise with the cursor line: 42 yards = 38.4 metres; 136 yards = 124.4 metres.
This example corresponds to normal cases as in basic rule (I).
The following examples can only be dealt with in accordance with basic rule (II) and by
the aid of the red index-mark.
| Examples: "Unit Value": 1" = 2.54 cm.
("Equivalence":26" = 66 mm); The red index-mark on W1 is placed opposite the value 2·54 on W1 the inches can now be read on W1' and W2' and the cm on W1 on W2. 20" = 50.8 cm; 40 cm = 15.75". |
Exchange rate: $ 1 = DM 4.00. The value 4·00 on W2 is placed opposite the red Index-mark; the DM can now be read on W1 and W2 and the $ on W1' and W2': $ 1-50 = DM 6·00; $ 2·26 = DM 9·04; DM 7·40 = $ 1.85; DM 10 = $ 2.50. |
 |
|
Squares and Square Roots
Squares of numbers are found by changing over from the W scales to the C scale situated on the centre of the tongue, using the cursor line.
Examples:
1.662 = 2.76. Place the cursor line on W1.1·66, and find the square (2.76)
above it, on C or on D. 5·252 = 27.6. Place the cursor line on W2-5·25, and
find the square (27.6) underneath it, on C or under it, on D.
Examples for practice: 67·32 = 4530; 10·73 = 114.5; 2·33 = 5.29; 1.3452 = 1.81; 7·472 = 55.8
To find square roots, the setting is carried out on C, on the middle of tongue, or on D, with the aid of the cursor line, and the square-root is then found on scales W2' or W1', likewise underneath the cursor line. It should be noted that the roots of numbers from 1 to 10 will be found on the W1 scale and those of numbers from 10 to 100 on the W2 scale.
Examples:
Ö 4.56= 2.135. Cursor line on C-4·56 (or D 4-56); the result
(2.135) will be found below it, on W1' or W1.
Ö56 = 7.483. Cursor line on C·56 (or D 56); the result
will be found above it, on scale W2' or W2.
To extract roots of numbers under 1 (e.g. 0.76) or above 100 (e.g. 2375) with greater ease, suitable powers are separated from the radicand.
Example:
Ö0.76 = Ö(76 / 100) = Ö76 / 10 = 8.72 / 10 = 0.872; Ö275 = Ö100 x Ö2.75 = 10 x Ö2.75
= 10 x 1.658 = 16.58
Ö2375 = Ö(100 x 23.75 = 10 x Ö23.75 = 10 x 48.75; Ö0.00387 = Ö(37.8/100000 = Ö37.8 / 100 = 6.15 / 100
= 0.0615
When using the root scales for calculation of squares and square roots, calculations can always be continued.
| 0.5735 x Ö(26.26/15.05) = 0.7575 | Cursor line on D 26.25; C 15.05 under cursor line; now place cursor line above W2-0·5735, and also read off the result, 0.7575, underneath the cursor line. |
| 52.752 x 0.0243 / 4.933 = 2.782 | Cursor line on W2 52.75, then W2' 4.93 under cursor line, then cursor line on C 0.0243, and also read off result, 2-782, on D, underneath the cursor line. |
| 6.34 x 25.45 / 3.2523 = 15.25 | Cursor line above D 6.34, then W1 3.252 under cursor line, then cursor line above C 25.45, and also read off result, 15.25, on D, underneath the cursor line. |
Calculations with the Mantissa Scale L
This scale operates in conjunction with the W scale, in this connection, attention should be paid to the zero position of the slide rule:
(I) When setting the antilogarithm on the lower root-scales W1', W1, the mantissa is read by means of the characteristic found to the left of the dividing-mark with the relevant subsequent graduation-marks to the right.
Example: log 1.35 = 0.1303. Cursor-line on W1-1·35; the figure .1 is found above it, to the left of the dividing-mark; in addition, we have 3 places of decimals and the exact setting 03. Thus, log 1.35 = 0.1303.
Examples for practice: log 2.655 = 0.424; log 0.237 = 0.3747 - 1; log 1938 = 3.2875; log 0.0119 = 0.0755 - 2
(II) When setting the antilogarithm on the upper root scales W2', W2, the mantissa is read by means of the characteristic found to the right of the dividing-mark, with the relevant subsequent graduation-marks to the right. Example: log 57.3 = 1·758. Cursor line on W2-57·3; the figure ·7 Is found underneath it, on the right of the dividing mark; in addition we have 5 decimal places and the exact setting 8. Thus log 57.3 = 1.758.
Examples for practice: log 9·06 = 0.957; log 0.0636 = 0.8034 - 2; log 445 = 2.6484; log 66·5 = 1.823.
If the mantissa is known, the converse process provides the antilogarithm sought. The logarithms enable the types of calculation to be reduced by one stage; multiplication and division thus become addition and subtraction, while the raising of numbers to powers or the extraction of roots becomes multiplication or division respectively.
For example: 2453.24 = 3.24 x log 245 = 3.24 x 2·389 = 7·74; 2453.24
= 55 000 000
420x = 10000; x x log 420 = log 10000; x
= lg 10000/lg 420 = 4.0/ 2.623 = 1.525
The Exponential Scales LL1
LL2 and LL3 for positive exponents;
LL01 LL02 and LL03 for negative exponents
The back of the slide rule has two four-stage groups of scales for the exponential functions, which are based on the basic scale C and D. The scales for positive exponents (black) extend from 1.00088 to 60000, while those for negative exponents (red) extend from 0.00002 to 0·999. The e-x scales are reciprocal scales for the ex scales. In this connection it should be noted that the numerical values given on the exponential scales do not change where the decimal places are concerned; thus, "1·04" Invariably signifies 1.04 - not 10.4, 104, etc.
When changing over from an internal scale to the next one, proceeding outwards, the
exponential scales give powers of ten, e.g. -
0.95510 = 0.631; 0.63110 = 0.01; 0.92410 = 0.454; 0.45410
= 3·7 x 10-4 = 0.00037
1.047210 = 1.586; 1.58610 = 101; 1·0810 = 2·16; 2.1610
= 2·2 x 103 = 2200
When changing over to the next but one, proceeding outwards, one obtains powers of a
hundred, e.g. -
0.95510 = 0.01; 1·04715100 = 100; 0·924100 = 3.7 x 10-4
= 0.00037; 1·8100 = 2200
When changing over from an outer to an inner scale, one obtains the corresponding
roots, e.g. -
10Ö0.25 = 0.8705; 10Ö0.8705
= 0.98623; 100Ö0.25 = 0.98623 ; 10Ö0.00007 = 10 (7 x 10-5) = 0.384; 10Ö0.384 = 0.9087; 100Ö0.00007
= 0.9807
10Ö4 = 1.1488; 10Ö1.1488
= 1.01396; 100Ö4 = 1.01396
10Ö15000 = 10Ö(1.5
x 104) = 2.616; 10Ö2.616 = 1.1009; 100Ö15000 = 1.1009
Note the following:
| At 100 on the LI3 Scale, the LL02 scale shows the value of - = 0.01 | since e-x = 1/ ex |
| At 1.25 on the LL2 Scale, the LL02 scale shows the value of = 0·8 |
Exponential scale LL0 for e0.001x
As the values of the D scale are almost identical with those of the e0.001 scale, the exponential scale LL0 has been incorporated in scale D. Up to the value e0.003 = 1·003, the deviation is only 0.000 005. Beginning with 00.004, correction is provided in that the actual value is shown in oblique figures at the right hand of the numbers pertaining to scale D.
The Natural Logarithms
The natural logarithms are found by setting the antilogarithm with the long
cursor line on the LL Scales and by reading off the mantissa, likewise underneath the
cursor line on D, or (in the case of the zero position) on C. The foregoing applies,
mutatis mutandis, to the "place-of-decimal ranges".
Example: Ln 25 = 3.22; Ln 145 = 4.97; Ln 1.3 = 0.262; Ln 0.04 = - 3·22; Ln
0·66 = - 0·416; Ln 098 = - 0·0202.
Powers of e
The powers of e (base of natural logarithm e = 2.71828 . . .) are obtained by
setting the exponent, by means of the cursor line, on scale D or (by zero-ing) scale C.
The e power is then found on the LL scale. In this connection the range for the D scale
and C scale is 1 -10 at LL3, 0.1 -1 at LL2 and 0.01 -0·1 at LL1.
Example: e1·61 = 5; set cursor line over D 161, find result on LL3 5.
In the same way (at zero position) one can also set the cursor line over D, instead of C.
Further examples:
e0·161 = 1.175; e0·0161 = 1.01622; e6·22 =
500; e0·622 = 1.862; e0·0622 = 1.0642;
e12·5 = e10+2.5 = e10 x e2.5 = 22,000 x 12.2
= 268,400.
In case of negative exponents, one uses the negative exponential scales LL03, LL02, LL01, LL0.
Example: e-1.61 = 0·2; set cursor line over D 161, find result 0.2 on 1103.
In the same way (slide at zero position) one can also set the cursor line over D, instead of C.
Further examples: e -0·161 = 0·8512; e-0·0161 = 0·984; e-6·22 = 0.002; e-0·622 = 0·537; e-0·0622 = 0·9397.
In forming the hyperbolic functions, the argument x is fixed on the C scale with the aid of the cursor.
On the ex and e-x scales, reading can then be taken of the e
powers. Half the sum (or difference) then gives the
cos h (or sin h), e.g. -
cosh 35° = cosh 0.61 = (ex + e-x) / 2 = (1.84 - 0.543)/2 =
1.1915
sinh 35° = sinh 0·61 = (ex - e-x) / 2 = (1.84 + 0.543)/2 = 0.6485
We express the root as a power with a reciprocal exponent and then proceed as above (under powers of e).
Example:
4Öe =e0.25 = 1.284; 0.25Öe = e4 = 54.6; 8Öe
= e0.125 = 1.135; 0.125Öe = e8
= 2980
12.5Öe = e0.08 = 1.0834; 0.06Öe = e16.66 = e8.33 x e8.33 = 4146
x 4146 = 17 189 000
Powers of the form an are obtained by moving C-1 into position above the
basic value, a, of the corresponding LL scale, after which the cursor is moved to C-n. The
value of an can then be found on LL, e.g. -
3·752.96 = 50. Cursor above LL3 - 3-75, CI under cursor line; then
cursor line above C 2.96, and read off the result, 50, on LL3.
Further examples:
4.22·16 = 22·2; 4.20·216 = 1·364; 4.20·0216 = 1.0315
4.2-2.16 = 0·045; 4.2-0.216 = 0.7335; 4.2-0·0216 =
0·96945
By means of the LL03 scale:
0·052.16 = 1·55 x 10-3 = 0·00155
0·050·216 = 0.524; 0.050·0216 = 0.9374
0.05-2·16 = 1 / 0·050·216 = 646 (reading to be taken
on the LL3 scale).
0.05-0.0216 = 1 / 0.050·0216 = 1.91 (reading to be taken on the LL2
scale).
As regards the places of decimals, see remarks under "Powers of e."
With the aid of the cursor line, place the root-exponent on C above the root-number on LL (first finding the root-number and placing the cursor line above it); the result is then found underneath C 1 or C 10.
Example:
4.4Ö23= 2.04. Cursor line above LL3 -
23, C 4·4 under cursor line, then cursor line above C 10, and read off the result, 2.04,
underneath it, on LL2
Examples
2.08Ö1.068 = 1.03216 (place C -2·08 above LL1-1·068,
take reading on LL1).
0.6Ö15.2 = 93·5 (place C-0·6 above LL3-15·2,
take reading on LL3).
20Ö4.41= 1.077 (place C-20 above LL3-4·41,
take reading on LL1).
5Ö0.5= 0.8705 (place C-% above LL02-0·5,
take reading on LL02).
50Ö0.5= 0·98622 (place C-50 above 1102-0·5.
take reading on LL01).
Further examples:
5Ö2 = 1.148; 5Ö20 = 1.82
0.06Ö2.42 = 2.4216.66 = 2.428.33
x 2.428.33 = 1580 x 1580 = 2 486 400
Place the cursor line above LL3-10 and C 1 of the central tongue-scale underneath the cursor line. This provides a table of the logarithms to base 10. It can also be set, however, by placing C 10 above LL3-10.
Settings and readings can now be carried out by the aid of the cursor.
log 10 = 1; log 100 = 2; log 1000 = 3; log 200 = 2.301
log 20 = 1.301; log 2 = 0.301; log 1.1 = 0.0414.
By means of the LL03 scale:
log 0.1 = -1; log 0.01 = -2; log 0.001 = -3.
log 0.2 = -0.699 = 0.301-1; log 0·05 = -1·301 = 0699-2.
Production of Logarithmic Diagrams to any desired scale.
When diagrams are produced with a logarithmic graduation, it is often necessary to solve y = a log x. (a = scale-factor = length of logarithmic unit). We cannot change over from C to L, since no further multiplications can be carried out on the linear L series. On the other hand, of course, the change-over from LL to D corresponds to the operation of forming the logarithm, and the C scale can then be used for further multiplication.
Example: a = 3·33; x = 2; 3; 4; 6.
With the cursor line place C ·33 above LL3 10 (logarithmic unit) and find,
with LL3 or LL2 2; 3..., the relevant y-values
on the C scale. y = 1·002; 1·591; 2·003; 2·593.
If necessary, push the slide through. A little thought will enable errors as regards the place of decimals to be avoided.
Logarithms to any desired base
Place the beginning of the C l or C 10 above the base on the LL scale; this provides a
table of the relevant logarithms, e.g.
2log 200 = 7·64; 2log 22 = 4·46; place C 10 above 112.2; find the
value 7·64, at LL3-200, on C, and the value 4·46, at LL3-22, on C
(all by the aid of the cursor line).
Further examples:
2log 1·2 = 0·263; 0·2log 10 = - 1·431; 0.8log
2 = - 3·11; 5log 25 = 2; 0·51og 25 = -
4·64;
Note the following:
alog a = 1; e.g.: 2log 2 = 1; 2Iog 4 = 2; 2log
8 = 3
0·51og 0·5 = 1; 0·5log 4 = - 2; 0·51og
8 = - 3
0·51og 0·25 = 2; 0·51og 0.25 = 3
The value p = 3·1416 is specially marked on the scales C, D, CI, CF. DF, CIF, W1, W1', W2, W2'. This makes the value far easier to find and set.
Mark r = 0·01745 on the scales C, D, W1, W1' (see above).
The ST scale for small angles contains so-called correction-marks in the range 4°-6°,
which give the correct functional values for sine and tangent.
Examples: tan 2·5° » sin 2·5° = 0·0436; tan 4° » sin 4° = 0·0697.
For an exact reading the tangent 4°, the correction mark to the right of the graduation
mark 4° is used. A reading is taken of 0·0699.
For the correction-marks of the tangent we thus have: Tangent greater than arc, therefore
correction-mark to the right of the graduation-mark.
Example: tan 5° = 0·0875.
If the angle is Intermediate between full degrees having correction-marks, then the
correction-interval must be transferred accordingly.
Example: tan 3·5° = 0·0612; tan 4·2° = 0·0734; tan 5·33° = 0·0934.
If the functional value is known and the angle is required, the correction-interval .to
the loft is taken into account.
For the sine, the correction-mark is provided to the left of graduation-mark 6°. It
applies to the range 5°-6°.
Proceed in this case as in the foregoing, only in the opposite direction.
Mark e = 2·71828 (base of the nat. log) on the scales LL2 and LL3.
The Cursor
| The two-sided cursor has a long central line on the front and back, to enable settings to be carried out and readings to be taken in ordinary continuous calculations; it also has the red side-marks on the right-hand and left-hand edge, for reading values on the extended red supplementary graduations which the central cursor line cannot reach. | 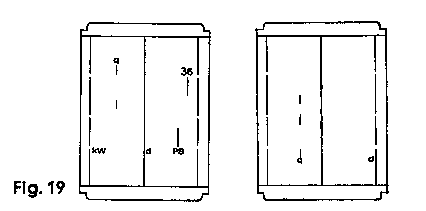 |
The fields of application for the remaining marks are as follows:
Calculation of the area of a circle, on front of slide rule (d, q)
Set the central main cursor line (d) over the diameter on scales D or C and find the
relevant area on scales A or B, under the two short cursor lines in the upper left hand
corner.
Calculation of the area of a circle, on back of slide rule (d, q)
Conversion of horsepowers to kilowatts
Direct calculations with the factor 3·6.
The double cursor can be easily removed for cleaning, without interfering with the fine adjustment of the slide rule.
The Care of the Slide Rule:
CASTELL Slide Rules are valuable precision implements and require careful handling.
They are made of an ideal special plastic material. This is highly elastic and thus
unbreakable provided it is competently handled. It will stand up to climatic conditions;
it is moisture-proof and non-inflammable and will resist the majority of chemicals. These
slide rules should nevertheless not be allowed to come in contact with corrosive liquids
or powerful solvents, which are at all events liable to attack the colouring-agents
applied to the graduation-marks, even if they do not actually harm the material itself. If
necessary, the smooth movement of the slide can be improved by the use of Vaseline or
silicon oil. In order not to detract from the accuracy of the readings, the scales and the
cursor should be protected from dirt and scratches and should be cleaned with the special
cleaning agents CASTELL No. 211 (liquid), or No. 212 (cleaning paste).