Electrical Slide Rules

Background

Electrical slide rules were designed to perform two types of calculations:

• Efficiency of motors and dynamos
• Voltage loss in cables.

For motors the efficiency was the ratio of the mechanical energy output divided by the electrical energy input; in the case of dynamos it was the ratio of the mechanical energy input divided by the electrical energy output. Apart from the fact that the units of energy were different, horse power for mechanical energy and watts for electrical energy, the calculation was basically very simple.

The calculation of voltage loss in cables was not much more complicated. The voltage loss was given by ohms law:

    volts = current (amps) * resistance (ohms)

The resistance was given by:

    resistance (ohms) = length * resistivity / sectional area.

In metric units the dimensions of resistivity are ohms metre.

There are however a few complicating factors that users of rules should be aware of:

• There were two different units for horse power. The first, used in the UK/US, was based on the energy to lift a 550 pound weight through 1 foot in one second and was equivalent to 746 watts; the second, used in continental Europe, was based on the energy to lift 75 kilograms through 1 metre in 1 second and was equivalent to 736 watts. The latter is sometimes marked as PS, from the German Pferdestärke.
• Different units of area were used. Normally in the metric system the sectional area of the cable was square millimetres, in the UK/US system it could be either square inches or circular mils. The latter was a slightly unusual unit in that it was based on the diameter in 1/1000s of an inch squared. In the US gauge sizes were sometimes used.
• Since calculations using basic units (e.g. 1 square inch and 1yard) would result in voltage values very different to those found in real life, the rules were usually set up for a combination of more usual units (e.g. 10 mm² and 10 metres).
• Although in the above equation the resistivity is used, the use of the inverse, the conductivity, was more common.
• The resistance of a metal varies with temperature. Sometimes the resistivity/conductivity is expressed as the value at 0 °C ( 32° F) and at other times at 20 °C (68° F). Typical values of resistivity for copper are 1.56 * 10^-8 ohms metre at 0 °C and 1.67 * 10^-8  at 20 °C . The equivalent values of conductivity are 6.41 * 10⁷ and 5.98 * 10⁷. On some rules there is a gauge point at 28.7 which is considered to be 0.5 * conductivity. Which does not quite agree with the figure of 5.98; another complicating factor and one I can not yet explain.
• Some rules have gauge points for the use of metals other than copper, for example aluminium.

The rules

These instructions are based on the rules listed below with their units of measurement :

Most of the rules have special scales for efficiency and voltage loss. Sometimes these are set in the well of stock The example below comes from the Thornton/PIC 131. The scales for efficiency are in the upper part (dynamo in black and motor in red). The lower scale is for voltage loss.

To read the values of the scales in the well of the stock,  a variety of different methods were used. Some of these were based on "chisel" type cursors (which owed something to the early cursors). I give below four variants. Of these the most convenient is the latest of them - on the Thornton 131. The fourth image, the Aristo, was provided after I had developed this site and has a similar cursor to the Thornton. On this rule it is possible to see not only the cursor but also the mark D/M for dynamo/motor efficiency and different gauge marks for Copper (Cu) and Aluminium (Al) wire.

Thornton/PIC 4866

Faber Castel 398

Thornton 131

Aristo Elektro

Other rules had the efficiency and voltage scales set below the principal scales. The example given below is from the Graphoplex Electro. The W&G 432 used a similar approach.

The Unique is the only one which does not have special scales for efficiency and voltage, relying instead on gauge points.

Most of the rules have additional scales for the change of resistance with temperature. Those on the Unique Electrical were particularly extensive covering the range from 0 °C to 300 °C.

The above image also shows the gauge point marked W used for efficiency calculations.

Most of the rules also mark the scales to be used for kW and HP or PS. In passing it is interesting that the French rule also uses PS rather than the French equivalent CV (chevaux vapeur).

I have to confess to being unsure as to why electrical rules often had the scales in the well of the stock, particularly as the Unique manages perfectly well without them. One theory on the egroups forum was the it meant a basic design of stock and slide could be used without the need for re-tooling;  a more cynical explanation was that it was done to make them look more special and so attract a premium price!

Dynamo Efficiencies

The basic equation is:

    Efficiency = Electrical energy output / Mechanical energy input.

Example:
   Calculate the efficiency of a dynamo which gives an output of 13.5 kW for 21.0 H.P.

Faber Castell Elektro
   Set 2.10 on the B scale against 13.5 on the A scale.
   Read the efficiency, 86.2% on the Dynamo efficiency scale.

As a check, 21.0 multiplied by .746 is 15.67 and 13.6 / 15.67 is 86.2

Most of the other rules, including those with the scale to one side operate in the same way. For example the same calculation is shown below on the Graphoplex.

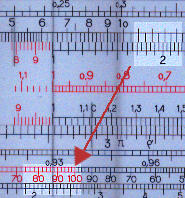
It will be seen that the answer is not the same as the above. This is because the Graphoplex used the continental horse power. The answer in this case is 88%.

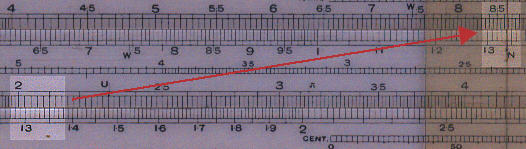
To perform the same calculation on the Unique Electrical it is necessary to use gauge points.

    Set 33.4 on D scale against 51.6 on C scale.
    Read the efficiency, 86.6% on the d scale, opposite the gauge point N on the c scale.

Motor Efficiencies

In this case the basic equation is:

    Efficiency = Mechanical energy output /Electrical energy input.

Example:
   Calculate the efficiency of a motor which develops 150 H.P. for 128 kW.

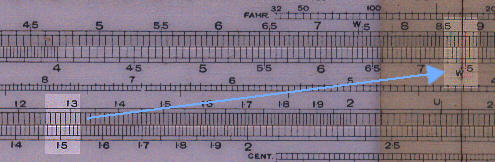
Since for most rules the calculations of motor efficiency are simple mirror of the calculations for dynamo efficiency I give below the method for the W&G 432.

   Set 128 on the kW scale against 150 on the HP scale.
   Read the efficiency, 87.5% on the Motor efficiency scale, opposite the gauge point.

For an example of the calculation on a rule with scales in the well of the stock I will consider a Thornton 131.
   Set 150 on the HP scale against 128 on the kW scale.
   Read the efficiency, 87.5% on the Motor efficiency scale.

Finally let us carry out the calculation on a Unique. Set the horse power on the D scale against 128 on the C scale. Read the answer, 87.5%, on the d (equivalent to the DF scale) or D scale opposite the " gauge mark.

Voltage Drop

Background

Voltage drop is given by the formula:

    V = (I x L )/ (c x A)
Where:
    V is voltage drop (volts)
    I is the current (amps)
    L is the length (yards)
    C is the conductivity of copper
    A is the section of the conductor. Typical units for this are square inches, square millimetres and circular mils. Circular mils is calculated from the diameter of the wire in thousandths of an inch squared.

The calculations all assume copper wire.

Example:
Calculate the volt drop in a copper conductor 131 (119.7 m) yards long, 0.14" (3.56 mm) diameter, carrying a current of 20.4 amps.

The area of a wire 0.14 diameter is .0154 in² , equivalent to 9.94 mm² and 19600 circular mills (=140 * 140).

Thornton PIC 131

The Thornton is set up for current in units of 10 amps, lengths in units of 10 yards and areas in units of .01 sq. in. So:
    Align 1 on the B (length and area) and scale against 2.04 (2.04*10amps = 20.4 amps) on the A (current) scale.
    Cursor to 13.1 (13.1 * 10 yards = 131 yards) on the B (length and area) scale.
    Align 1.54 (1.54 * .01 sq. in = .0154 sq.in).on B (length and area)scale.
    Read the answer 4.24 volts in the well of the stock.

Faber Castell 1/98

The Faber Castell 1/98 is set up for units of 10 amps, 10 yards and 10000 circular mils.
    Align 1 on the B (length and area) and scale against 2.04 (2.04*10amps = 20.4 amps) on the A (current) scale.
    Cursor to 13.1 (13.1 * 10 yards = 131 years) on the B (length and area) scale.
    Align 1.96 (1.96 * 10 000 circ. mils = 19600 circ. mils)on B (length and area)scale.
    Read the answer 4.14 volts in the well of the stock.

Faber Castell 378

The Faber Castell 378 is set up for units of 10 amps, 10 metres and 10 mm².
    Align 1 on the B (length and area) and scale against 2.04 (2.04*10amps = 20.4 amps) on the A (current) scale.
    Cursor to 13.1 (11.97 * 10 metres = 119.7 metres) on the B (length and area) scale.
    Align 0.994 (0.994 * 10 mm² = 9.94 mm² ) on B (length and area) scale. The "volt" cursor is past the end of the rule so align the cursor with 100 and the move the slide so that the 1 aligns with the cursor.
    Read the answer 8.5 volts in the well of the stock.

As can be seen the answer is twice the value given by the other rules and should be multiplied by 0.5. This appears to be a common feature of all "metric" electrical rules. A similar result is obtained using the Graphoplex.

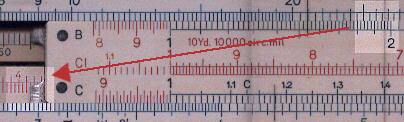
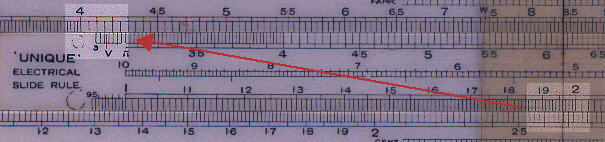
Unique Electrical
   Area is 140² = 19600 circular mils.
    Set 1 on C against 2.04 on D.
    Move cursor to 1.31 on C.
    Move 1.96 to the cursor.
    Read volt drop, 4.16, above V on the c scale.

W&G 432

    Align 1.54 on area/length scale against 2.04 on current scale.
    Align cursor with 131 on area/length scale.
    Answer 4.19 volts under cursor on volt scale.

Variation of resistance with temperature

To solve:
   A copper wire has a resistance of 2.8 ohms at 20 ° C (68 ° F). What is its resistance at 5 ° C (41 ° F) and 104 ° F (40 ° C).

Unique Electrical
   Set cursor to 20 ° C on lower temperature scale.
    Set 28 on C scale to cursor.
    Move cursor to 5 ° C on lower temperature scale.
    Read 2.63 ohms under cursor on C.
    Move cursor to 104 ° F on upper temperature scale.
    Read 3.01 ohms under cursor on C.

Faber Castell Elektro
   Set the cursor to 2.8 on the A scale.
    Set 68 ° F on the temperature scale to the cursor.
    Move the cursor to 41 ° F (= 5 ° C).
    Read 2.63 ohms under cursor on A.
    Move the cursor to 104 ° F.
    Read 3.01 ohms under cursor on A.